
空间汇交力系 (9) 第三章空间力系 空间力偶系 (§3-1空间汇交力系:安排自学) (空间任意力系 s3-2力点之矩和力对轴之矩(空间问题) 1、力对点之矩一力矩矢 Mo(F) Mo(F=Fh=F·rsina(两倍△0AB的面积卡 Mo(F)=F×F(定位矢量) 19 空间问题力对点之矩以“矢量”表示 平面问题力对点之矩以“代数量”表示 2、力对轴之矩 M.(F)=M,(F)+M.(瓦)(由合力矩定理) 即M(同=M.(低)=,h厂代数量 气"士”:右手定则 结论:力对轴之矩等于力在垂直于该轴平面上的分力对该轴与平面交点之矩。 (力对轴之矩与平面问题中的力对点之矩相对应,其“±”号规定也相对应。) 「力与轴平行 有{方与轴相交力对之矩为零。介绍开门实》(又:教材种的力对轴之矩的解折表达式略) M(F)=M.(F) 3、力对点之矩与力对轴之矩的关系式:了[Mo(F)=M,(F) M(F).=M.(F) 例:曲轴位于xOy平面。求:M(F),M,(F),M.(F)(介绍“手抓法) 解: F=Fcosasino ①求各分力大小了F,=Fcos a cos F.=Fsina 0 M(F)=-Fsin·b ②求对各轴力矩 M,(F)=-Fsina.a M.(F)=-Fcosasinp.b+Fcosacos.a
1 ( ) FxFxFx x y z i j k 第三章 空间力系 (§3-1 空间汇交力系:安排自学) §3-2 力点之矩和力对轴之矩(空间问题) 1、力对点之矩 — 力矩矢 MO (F) Fh F rsin (两倍△OAB 的面积) MO (F) r F (定位矢量) 空间问题力对点之矩以“矢量”表示 平面问题力对点之矩以“代数量”表示 2、力对轴之矩 0 ( ) ( ) ( ) M z F M z Fxy M z Fz (由合力矩定理) 即: M z (F) M z (Fxy ) Fxy h 结论:力对轴之矩等于力在垂直于该轴平面上的分力对该轴与平面交点之矩。 (力对轴之矩与平面问题中的力对点之矩相对应,其“±”号规定也相对应。) 有 力对轴之矩为零。(介绍开门实例) (又:教材中的力对轴之矩的解析表达式略) M (F) M (F) O x x 3、力对点之矩与力对轴之矩的关系式: M (F) M (F) O y y M (F) M (F) O z z 例: 曲轴位于 xoy 平面。求: M (F), M (F), M (F) x y z (介绍“手抓法”) 解: Fx F cos sin ①求各分力大小 Fy F cos cos Fz F sin M x (F) F sin b ②求对各轴力矩 M y (F) F sin a M z (F) F cos sin b F cos cos a α 力与轴平行 力与轴相交 αφ 空间汇交力系 (9) 空间力偶系 空间任意力系 注 代数量 "" :右手定则

§3-3空间力偶 ☆:力偶矩以矢量表示:三“力偶矩矢”:M(右手定则,“自由矢量”) 力偶矩大小 ”右手定则” 力偶三要素 力偶转向 力偶作用面方位 S3-4空间任意力系向一点简化·主矢和主矩 §3-5空间任意力系的平衡方程 空间汇交力系:主失:下=Σ下 1、空间任意力系向一点简化 空间力偶系:主矩:M。=∑应。(匠) ①下F阳=0,M。≠0→力系简化为一合力偶 ②F:≠0,M。=0→力系简化为一合力 2、简化结果分析了 ③下F=0,M。=0→力系平衡 人④F≠0,M。≠0→力系需进一步简化 「☆FR⊥Mo:→一合力 1☆其他情况: →力螺旋 3、空间任意力系的平衡方程 ∑F=0 ①空间汇交力系:“力矩式”自然满足 「FR=0 的 (6个) ∑M,=0 (分析 ②空间力偶系:“投影式”自然满足 〔。=0 (③平面任意力系:“?式”自然满足 (注:类似平面任意力系平衡方程有“二矩式”、“三矩式”,空间任意力系平衡方程也可取四到六个力矩式。) 例: 45 已知:曲轴位于x4少水平面, 60 F大小,方向已知。 A处为径向止椎轴承,B处为径向轴承。 求:平衡时P力大小及A、B两处反力。 解:整体→受力图 ∑F=0 Fx+F+Fcos60°sin45°=0 (共六个未知量) EF,=0Fy-Fc0s60°cos45°=0 ∑F=0-P+F+F-Fsin60°=0 ∑M=0 P40+60)-Fk·60-Fsin60°(30+40)=0 ∑M,=0P.40/2-Fsin60°.100=0 ∑M.=0F·60-Fcos60°sin4530+40)+Fcos60°cos45°.100=0
2 1、空间任意力系向一点简化 FR 0 Mo 0 §3-3 空间力偶 ☆:力偶矩以矢量表示: “力偶矩矢”: M (右手定则,“自由矢量”) 力偶矩大小 力偶三要素 力偶转向 力偶作用面方位 §3-4 空间任意力系向一点简化·主矢和主矩 §3-5 空间任意力系的平衡方程 空间汇交力系:主矢: FR Fi 空间力偶系:主矩: MO MO Fi ① FR 0, Mo 0 力系简化为一合力偶 ② FR 0, Mo 0 力系简化为一合力 ③ FR 0, Mo 0 力系平衡 ④ FR 0, Mo 0 力系需进一步简化 3、空间任意力系的平衡方程 由 (6 个) (分析 (注:类似平面任意力系平衡方程有“二矩式”、“三矩式”,空间任意力系平衡方程也可取四到六个力矩式。) 已知:曲轴位于 xAy 水平面, F 大小,方向已知。 A 处为径向止椎轴承,B 处为径向轴承。 求:平衡时 P 力大小及 A、B 两处反力。 解:整体 受力图 0 cos 60 sin 45 0 Fx FBx FAx F (共六个未知量) 0 cos 60 cos 45 0 Fy FAy F 0 sin 60 0 Fz P FBz FAz F 0 40 60 60 sin 60 30 40 0 M x P FBz F 0 40 / 2 sin 60 100 0 M y P F 0 60 cos 60 sin 45 30 40 cos 60 cos 45 100 0 M z FBx F F "右手定则" 例: 2、简化结果分析 ☆ FR MO : 一合力 ☆其他情况: 力螺旋 Fx 0 M x 0 ①空间汇交力系:“力矩式”自然满足 ②空间力偶系:“投影式” 自然满足 ③平面任意力系:“?式” 自然满足
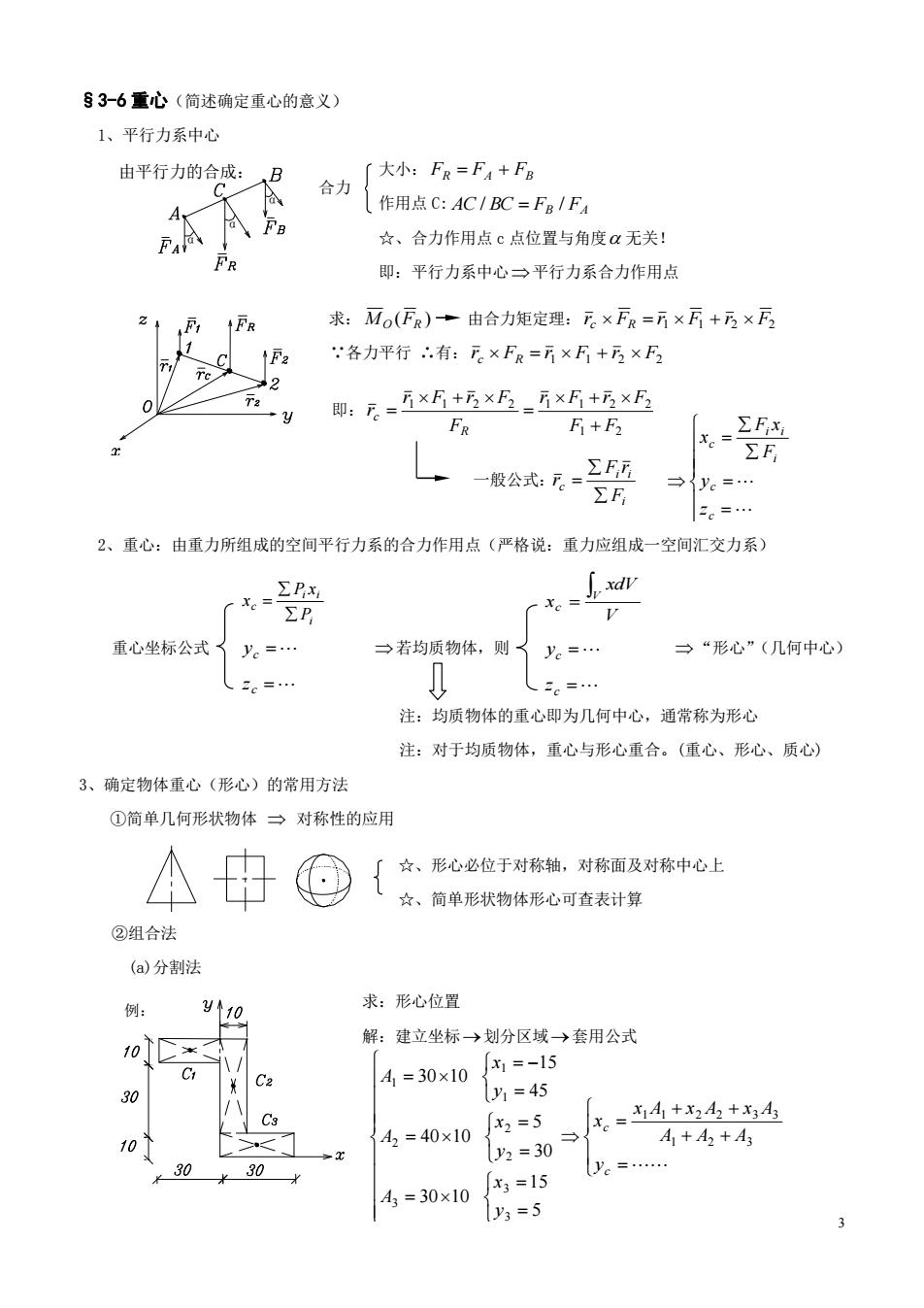
§3-6重心(简述确定重心的意义) 1、平行力系中心 由平行力的合成: 「大小:FR=FA+FB 合力 A 作用点C:AC1BC=FB/F 、F ☆、合力作用点c点位置与角度a无关! FR 即:平行力系中心一平行力系合力作用点 求:Mo(FR)+由合力矩定理:元×FR=斤×F+3×F 1F2 各力平行∴有:下×FR=万×F+万×F2 即:后=5×5+乃×5=万x5+5×5 FR F+F .-Efx E ,一般公式:元。=艺F ΣF y:=… 。=… 2、重心:由重力所组成的空间平行力系的合力作用点(严格说:重力应组成一空间汇交力系) ∑Px ∑P 重心坐标公式 →若均质物体,则了y。=… →“形心”(几何中心) 5e=… 注:均质物体的重心即为几何中心,通常称为形心 注:对于均质物体,重心与形心重合。(重心、形心、质心 3、确定物体重心(形心)的常用方法 ①简单几何形状物体一对称性的应用 A中@ 厂女、形心必位于对称轴,对称面及对称中心上 ☆、简单形状物体形心可查表计算 ②组合法 (a)分割法 例: y10 求:形心位置 0*≤ 解:建立坐标→划分区域→套用公式 c 4=30×10 x1=-15 1=45 10 4=40x10x3=5 4+4 A++A y2=30 30 30 ye=… A3=30×10 x3=15 1y3=5
3 即: 1 2 1 1 2 2 1 1 2 2 F F r F r F F r F r F r R c i i i c P P x x yc zc V xdV x V c yc zc c c y A A A x A x A x A x y x A y x A y x A 1 2 3 1 1 2 2 3 3 3 3 3 2 2 2 1 1 1 5 15 30 10 30 5 40 10 45 15 30 10 一般公式: i i i c F F r r c c i i i c z y F F x x §3-6 重心(简述确定重心的意义) 1、平行力系中心 大小: FR FA FB 作用点 C: AC BC FB FA / / ☆、合力作用点 c 点位置与角度 无关! 即:平行力系中心 平行力系合力作用点 求: ( ) MO FR 由合力矩定理: 1 1 2 F2 r F r F r c R ∵各力平行 ∴有: 1 1 2 F2 r F r F r c R 2、重心:由重力所组成的空间平行力系的合力作用点(严格说:重力应组成一空间汇交力系) 重心坐标公式 若均质物体,则 “形心”(几何中心) 注:均质物体的重心即为几何中心,通常称为形心 注:对于均质物体,重心与形心重合。(重心、形心、质心) 3、确定物体重心(形心)的常用方法 ①简单几何形状物体 对称性的应用 ☆、形心必位于对称轴,对称面及对称中心上 ☆、简单形状物体形心可查表计算 ②组合法 (a)分割法 求:形心位置 解:建立坐标 划分区域 套用公式 α α α 由平行力的合成: 例: 合力
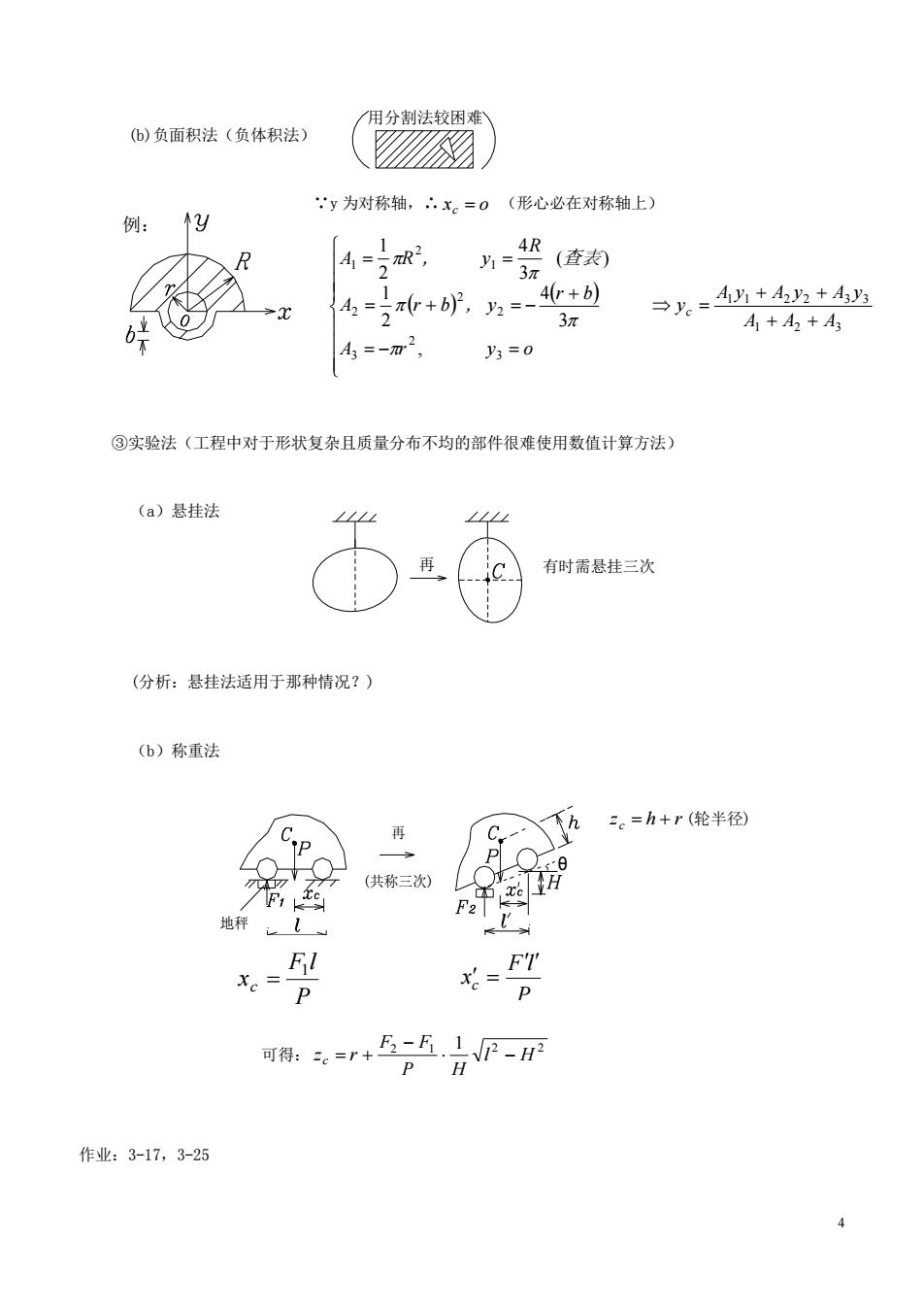
用分割法较困 (6)负面积法(负体积法) ☑ y为对称轴,x。=0(形心必在对称轴上) 1 A=2 R2, 4R =3 (查表) 4=+6,= 4r+b) →=4+4+4当 A+A2+A 4=-m2 =0 ③实验法(工程中对于形状复杂且质量分布不均的部件很难使用数值计算方法) (a)悬挂法 有时需悬挂三次 (分析:悬挂法适用于那种情况?)》 (b)称重法 C 。=h+r(轮半径) F:fe (共称三次) F21 xe=p 可得:e=r+5-E.是P-月 作业:3-17,3-25
4 A r y o A A A A y A y A y y r b A r b , y 查表 R A R , y c 3 2 3 1 2 3 1 1 2 2 3 3 2 2 2 1 2 1 , 3 4 2 1 ( ) 3 4 2 1 (b)负面积法(负体积法) ∵y 为对称轴,∴ xc o (形心必在对称轴上) ③实验法(工程中对于形状复杂且质量分布不均的部件很难使用数值计算方法) (a)悬挂法 (分析:悬挂法适用于那种情况?) (b)称重法 z h r c (轮半径) 作业:3-17,3-25 用分割法较困难 再 有时需悬挂三次 地秤 再 (共称三次) θ 例: P F l xc 1 P F l xc 可得: 2 1 1 2 2 l H P H F F z r c