
§7-4、牵连运动为转动时点的加速度合成定理·科氏加速度 (13) 「动点:M t时:下。=可。+, 不+△册T动系:AB牵:转动1+:=+ M Ma B 典-+ 「本老随魔:豆=一0 「≠。:(方向相同而大小不同) 注意 但有 人相度可-马” ≠可2(大小相同而方向不同) 利用-=何-)+-) -,=(-2)+(①2-,) 儿与得:a,=a,+a,+m+m二2 ac=2而×V, “科氏加速度”(附加加速度) 即:a。=a。+a,+a。有:a。=2而。×可,(可。:动系的角速度矢) (法国数学家:GCoriolis(1792-1843)1835年提出的) 注:a。=ā。+a,+a。:点的加速度合成定理的普遗形式(说明当牵连运动是平动时的特殊情况) Ur 而e a=2远x厂大小:a.=20.y5im0 (方向:由右手定则 ac ①若:可。与,垂直(即:可,在垂直转轴的平面内) 注(特例) 则:a。=2m。y,sin90°=2m., ②若:可。与币,平行(即:可,与转轴平行) 则:a。=0 例 北半球从南向北流动的河流, 产生向西岸的a。,(→a。=2而。×下,) 儿{“可由东岸对水的作用而产生 “东岸受到水的冲击(冲刷),长期会留下明显冲刷痕迹
1 有: t v v t v v t v v a r r t e e t a a t a 0 0 0 lim lim lim r r v v §7-4、牵连运动为转动时点的加速度合成定理·科氏加速度 动点:M t 时: a e r v v v 动系:AB(牵:转动) t t : a e r v v v c r a 2 v “科氏加速度”(附加加速度) 即: aa ae ar ac 有: c e r a 2 v ( e :动系的角速度矢) (法国数学家:G. Coriolis(1792~1843)1835 年提出的) 注: aa ae ar ac :点的加速度合成定理的普遍形式(说明当牵连运动是平动时的特殊情况) 大小: ac 2e vr sin 方向:由右手定则 ①若: e 与 r v 垂直(即: r v 在垂直转轴的平面内) 则: c e r e r a 2 v sin 90 2 v ②若: e 与 r v 平行(即: r v 与转轴平行) 则: ac 0 北半球从南向北流动的河流, 产生向西岸的 c a , ( 2 ) c e r a v ∵ c a 由东岸对水的作用而产生, ∴东岸受到水的冲击(冲刷),长期会留下明显冲刷痕迹。 时 △φ ω +△ 时 ω θ ω 例: ω (13) 牵连加速度: t v v a e e t e 1 0 lim 相对加速度: t v v a r r t r 2 0 lim 注意 e e1 v v (方向相同而大小不同) r r2 v v (大小相同而方向不同) 但有 利用 ( ) ( ) ( ) ( ) 2 2 1 1 r r r r r r e e e e e e v v v v v v v v v v v v 得: t v v t v v a a a r r t e e t a e r 2 0 1 0 lim lim c e r a 2 v 注(特例)
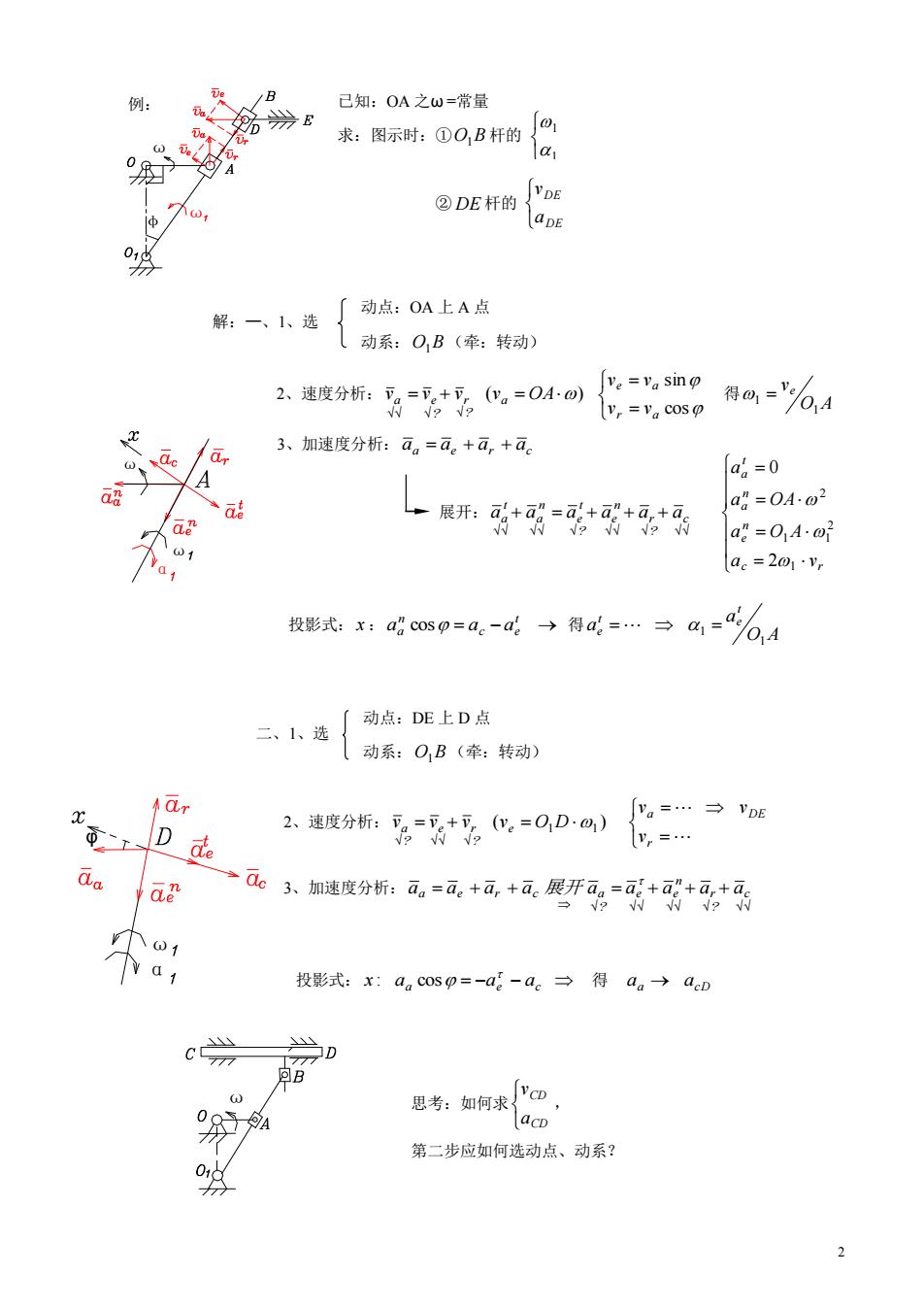
例: 已知:OA之W=常量 来:@08杆的份 ②DE杆的ape 解:一、、选厂动点:OA上A点 (动系:OB(牵:转动) 2速度分折:服=+化=04-) lvr=Va cos 得@='%,4 3、加速度分析:a。=a。+a,+a。 A a=0 、a话 上展开:耐+可的=+可,+ a=OA.02 a=0A.O a。=2m1, 二、1、选{动点:DE上D点 1动系:O,B(牵:转动) ar va=→vDE D de 2速度分析:3=+化,=0D:) y,=… dc 3、加速度分折:ā。=ā.+a+a,展开可+a+,+ā 个o1 投影式:x:acosp=-a-a。→得a。→aeD B 思考:如何求m acp 第二步应如何选动点、动系?
2 1 1 DE DE a v 1 1 2、速度分析: ( ) v v v va OA ? r ? a e cos sin r a e a v v v v 得 O A ve 1 1 投影式: x :aa n cos ac ae t 得 O A a a t e t e 1 1 展开: c ? r n e ? t e n a t aa a a a a a c r n e n a t a a v a O A a OA a 1 2 1 1 2 2 0 2、速度分析: ( ) 1 1 v v v ve O D ? e r ? a r a DE v v v 已知:OA 之ω =常量 求:图示时:① O1B 杆的 ② DE 杆的 动点:OA 上 A 点 动系: O1B (牵:转动) 3、加速度分析: aa ae ar ac 动点:DE 上 D 点 动系: O1B (牵:转动) 投影式: aa ae ac x : cos 得 aa acD 思考:如何求 CD CD a v , 第二步应如何选动点、动系? ω φ ω 例: ω α ω α ω φ ω 解:—、1、选 二、1、选 3、加速度分析: c ? r n e e ? aa ae ar ac 展开 aa a a a a
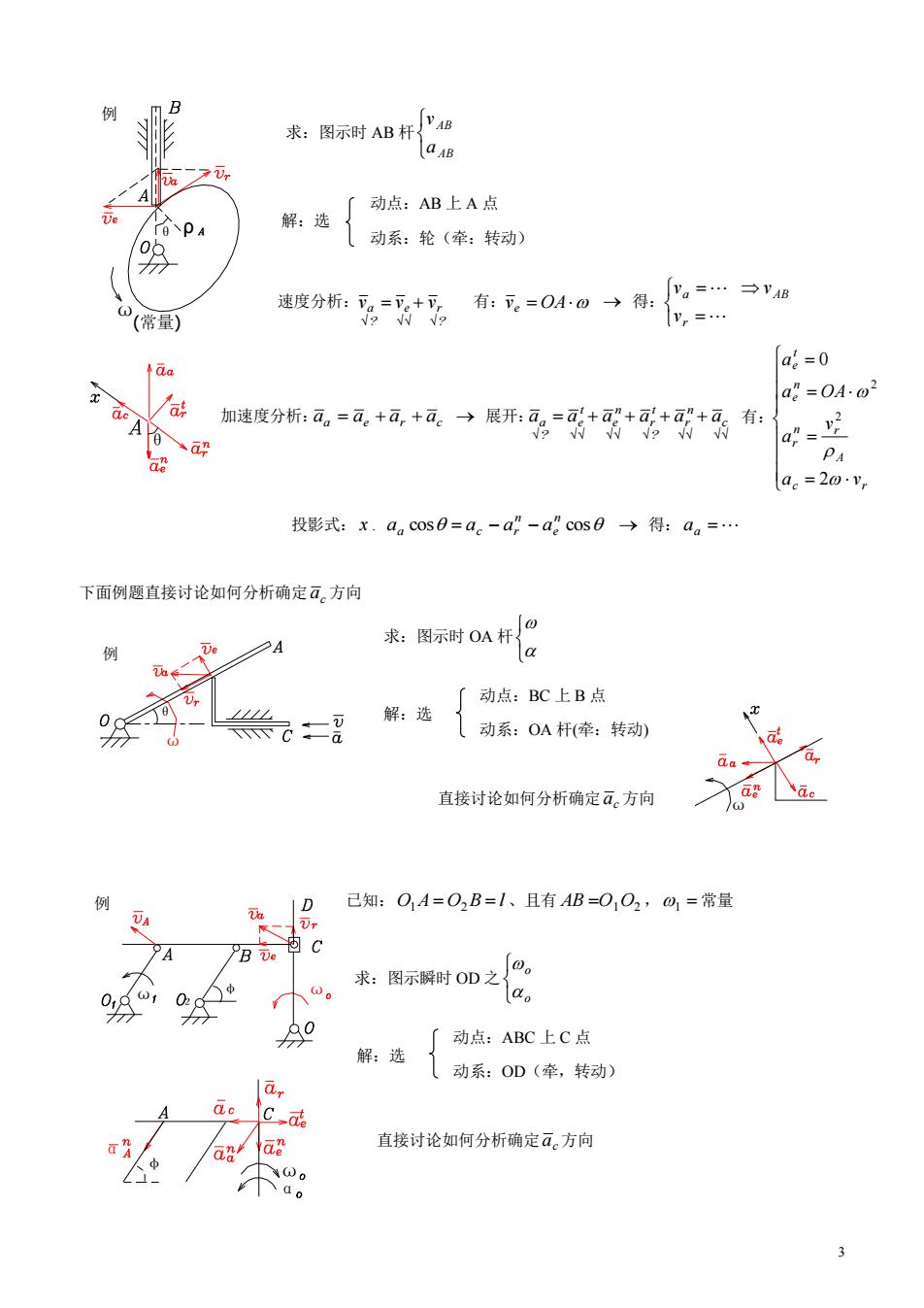
例 求:图示时AB杆a 之 解:送厂动点:AB上A点 0 动系:轮(牵:转动 0(常量) 速度分折:。=+ 有:。=040→得:。=…→B y,=… a=0 at a2=OA.02 加速度分析:可,=可++可。→展开:++计+有: a= PA a。=2oy 投影式:x.acos0=a。-a-acos0→得:a。=… 下面例题直接讨论如何分析确定ā。方向 例 求:图示时OA杆口 「动点:BC上B点 华。二 解:选 动系:OA杆牵:转动) 直接讨论如何分析确定ā。方向 1e. 已知:O,A=O2B=1、且有AB=O1,O2,01=常量 UA 阳c 求:图示瞬时OD之 la。 90 「动点:ABC上C点 a 解:选动系:0D(牵,转动》 a 直接讨论如何分析确定a。方向 不8
3 解:选 动点:AB 上 A 点 动系:轮(牵:转动) 投影式: x . aa cos ac ar n ae n cos 得: aa 下面例题直接讨论如何分析确定 c a 方向 动点:BC 上 B 点 动系:OA 杆(牵:转动) 直接讨论如何分析确定 c a 方向 已知: O A O B l 1 2 、且有 AB O1O2 ,1 常量 动点:ABC 上 C 点 动系:OD(牵,转动) 直接讨论如何分析确定 c a 方向 (常量) ρ ω θ 例 θ ω θ 例 ω ω 2 φ ω 例 φ ω α α 速度分析: ? e r ? a v v v 有: ve OA 得: r a AB v v v 求:图示时 AB 杆 AB AB a v 加速度分析: aa ae ar ac 展开: c n r ? t r n e t e ? aa a a a a a 有: c r A n r r n e t e a v v a a OA a 2 0 2 2 求:图示时 OA 杆 解:选 求:图示瞬时 OD 之 o o 解:选
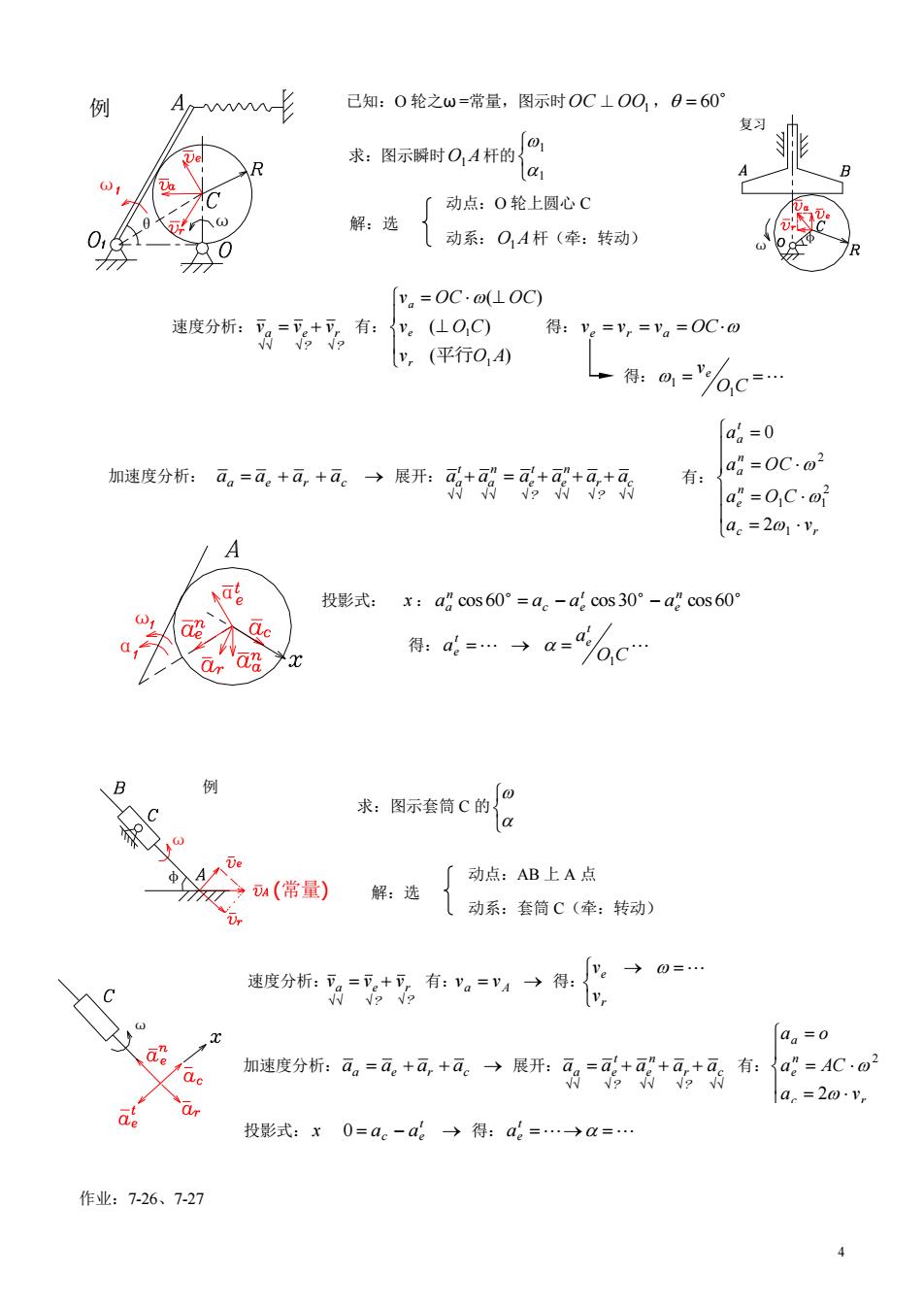
例 已知:0轮之w=常量,图示时OC⊥O0,0=60° 复习 求:图示解时04杆的@ 动点:0轮上圆心C 解:选 01 0 动系:O,A杆(牵:转动) [y。=OC·o(LOC) 速度分析:有 .() 得:=y,=。=OC0 y,(平行O4) 得:%= a6=0 加速度分析:a。=a.+a,+a。→展开:+=++ 有:a。=0co2 a=0,C·o ae=201y, A 投影式:x:acos60°=a。-acos30°-acos60° 得:d=…→a=4/ 求:图示套筒C的 入4 u(常量) 解:选 厂动点:AB上A点 动系:套筒C(牵:转动) 度分折=有:→得:化 →0= aa=o a 加速度分折:a,=a+a+a。→展开+矿+可。+及有:a:=Co la.=20.v, 投影式:x0=ae-a6→得:a6=…→a=… 作业:7-26、7-27
4 求:图示瞬时 O1A 杆的 1 1 得: O C a a t e t e 1 速度分析: ? r ? a e v v v 有: a A v v 得: r e v v 已知:O 轮之ω =常量,图示时 OC ⊥ OO1, 60 动点:O 轮上圆心 C 动系: O1A 杆(牵:转动) 投影式: x : cos 60 cos 30 cos 60 n e t c e n aa a a a 动点:AB 上 A 点 动系:套筒 C(牵:转动) 投影式: x 0 ac ae t 得: ae t 作业:7-26、7-27 ω 例 θ ω α α ω (常量) φ ω 例 ω 解:选 φ ω 复习 速度分析: ? r ? a e v v v 有: (平行 ) ( ) ( ) 1 1 v O A v O C v OC OC r e a 得:ve vr va OC 得: O C ve 1 1 加速度分析: aa ae ar ac 展开: c ? r n e ? t e n a t aa a a a a a 有: c r n e n a t a a v a O C a OC a 1 2 1 1 2 2 0 求:图示套筒 C 的 解:选 加速度分析: aa ae ar ac 展开: c ? r n e ? t aa ae a a a 有: c r n e a a v a AC a o 2 2