(4) $2-2平面力对点之矩.平面力偶 运动效应(外效应) 移动效应(取决于力的大小及方向) 力的效应 变形效应(内效应) 转动效应(引入力矩的概念和计算) 人方树点之矩功矩转司他{8的商《衡力胞物钠衡价南关 (历代数室伴面月题户{:生 (力F对点0之矩) (显然:当F=0 一M(匣=0:而h=0一表明力F作用线通过矩心) h=0 2、合力矩定理: 合力:F=∑F→力矩关系有:M(匠R上∑M(匠) 即:“合力之矩等于各分力之矩的代数和”(平面问题中) (解析表达式略》 例:皮带轮 Mo F=-Fr Mo(E上F2r 了:节圆半径(啮合圆) h 「啮合力:F 例:齿轮 求:Mo(F) 压力角:(啮合 法①:Mo(FFh=F·rcos0 法②:由合力矩定理:M(厅M(匠)+Mo(F)=Fcos0r M片 -P sin0.a M(@=-g212 Mg (PP sine-b 4合马B例: M@g22 思考题① 4 (MA()=? 思考题② A 出M4()=-
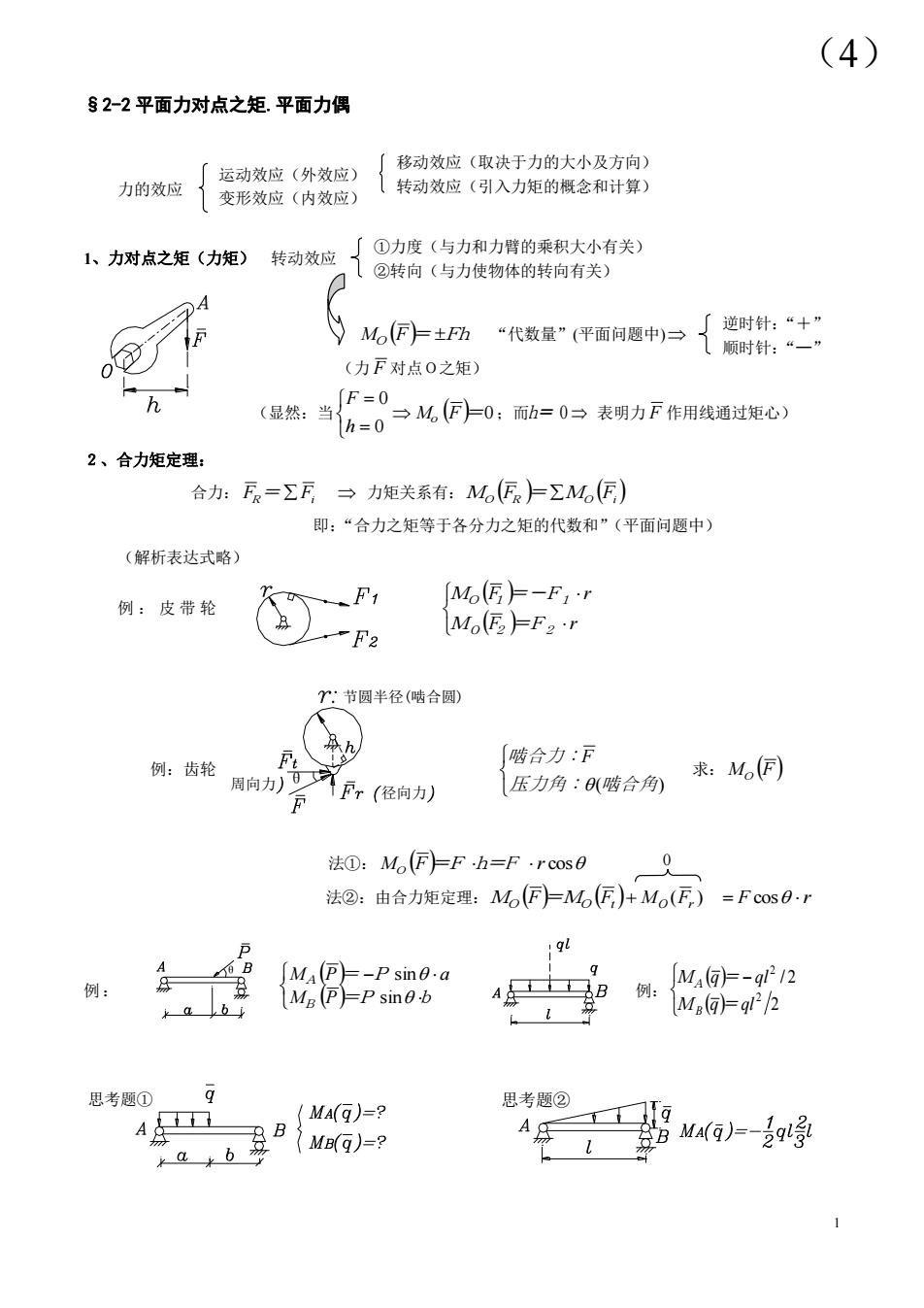
1 0 §2-2 平面力对点之矩.平面力偶 力的效应 1、力对点之矩(力矩) 转动效应 MO F= Fh “代数量”(平面问题中) (力 F 对点O之矩) (显然:当 0 0 0 M F = h F o ;而 h= 0 表明力 F 作用线通过矩心) 2、合力矩定理: 合力: FR = Fi 力矩关系有: MO FR = MO Fi 即:“合力之矩等于各分力之矩的代数和”(平面问题中) (解析表达式略) 例 : 皮 带 轮 M F =F r M F =-F r O 2 2 O 1 1 例:齿轮 压力角: (啮合角) 啮合力:F 求: M F O 法①: MO F=F h=F r cos 法②:由合力矩定理: ( ) MO F =MO Ft MO Fr F cos r 例: M P =P b M P = P a B A sin sin 例: 2 / 2 2 2 M q = ql M q = ql B A θ 径向力 节圆半径(啮合圆) 周向力 θ 思考题① 思考题② 运动效应(外效应) 变形效应(内效应) 移动效应(取决于力的大小及方向) 转动效应(引入力矩的概念和计算) ①力度(与力和力臂的乘积大小有关) ②转向(与力使物体的转向有关) 逆时针:“+” 顺时针:“—” (4)

补充介绍:两个平行力的合成①、同向 合力:E=F+EB 作用点:AC/BC=F/E:(内分线段) FB ②、反向CA-日°合力:=1 (条件:E≠Fa)FFA作用点:AC/BC=F,/BA(外分线段) 思考:若平行反向的两个力大小相等,结果应如何? 3、力偶与力偶矩: 力偶(F、F'):等值、反向但不共线的两个平行力,“特殊力系” F (注:力与力偶是静力学中的两个基本力学量,“广义力”) (①力偶不能合成为一个力(即:不能与一个力等效替换)[注:无合力与合力为零是不同的概念] 注: ②力偶不能与一个力平衡 ③力偶自身不能平衡 ④力偶只能与力偶平衡 女:力偶对物体(刚体)的转动效应 {力度一力偶矩:M(或M、F 1转向 力偶矩:M=±Fd(d:力偶臂) 代量{: 力偶矩:M=Fd 求:1 两力对平面内任一点之矩(之和):M(厅,F上M(厅+M(F) a (注意有无下标“o”区别) =F+d )-F'.x=Fd 即:M(F,F=M(∈M(F,F) 结论:力偶中两力对作用面内任一点之矩的代数和恒等于该力偶矩。 (力偶对刚体仅有转动效应。) 4、同平面内力偶的等效定理:“力偶矩相等(含大小及转向),力偶等效” 凸推论厂@方偶可能在其作用面内任意移转,面不改变对刚体的作用(与位置无关》。 (②只要保持力偶矩的大小及转向不变,可同时改变力偶中两力的大小和力偶臂的长短。 M 力偶表示方法: 5、平面力偶系的合成和平衡条件
2 力度 转向 补充介绍:两个平行力的合成 ①、同向 合力:FR=FA+FB 作用点:AC/BC=FB/FA(内分线段) ②、反向 合力:FR=∣FA-FB∣ (条件:FB≠FA) 作用点:AC/BC=FB/FA(外分线段) 思考:若平行反向的两个力大小相等,结果应如何? 3、力偶与力偶矩: 力偶( F、 F ):等值、反向但不共线的两个平行力,“特殊力系” (注:力与力偶是静力学中的两个基本力学量,“广义力”) ①力偶不能合成为一个力(即:不能与一个力等效替换)[注:无合力与合力为零是不同的概念] 注: ②力偶不能与一个力平衡 ③力偶自身不能平衡 ④力偶只能与力偶平衡 ☆:力偶对物体(刚体)的转动效应 力偶矩:M(或 MF、 F ) 力偶矩: M= Fd (d:力偶臂) 代数量 力偶矩: M Fd 两力对平面内任一点之矩(之和): M F, F =M F+M F O O O (注意有无下标“O”区别) =F x+d -F x=Fd 即: MO F,F=M ( M(F,F)) 结论:力偶中两力对作用面内任一点之矩的代数和恒等于该力偶矩。 (力偶对刚体仅有转动效应。) 4、同平面内力偶的等效定理:“力偶矩相等(含大小及转向),力偶等效” ①力偶可能在其作用面内任意移转,而不改变对刚体的作用(与位置无关)。 ②只要保持力偶矩的大小及转向不变,可同时改变力偶中两力的大小和力偶臂的长短。 力偶表示方法: 或 例: 5、平面力偶系的合成和平衡条件 例: 求: 逆时针:“+” 顺时针:“—” 推论
①合成:合力偶矩:M=∑M ②平衡:∑M=0(或:∑M=0) 求:A、B两处反力 解:AB→受力图→平衡方程 :主动力为力偶 A、B两处反力必组成一力偶与主动力偶M平衡 由平衡方程∑M=0-M+F1=0 有(仁6=兴 a哪个结构A处约束反力大? B① b b M 已知:M,r及0 A M大小 求:图示位置平衡时 O.B两处反力 ①轮0 ∑M=0 M,-Frsi=0 FA Fo 得E,==Mne ②杆BCC M2 zM=0-场+i0 A 得:M2=… 且有:FB=F=F4=F
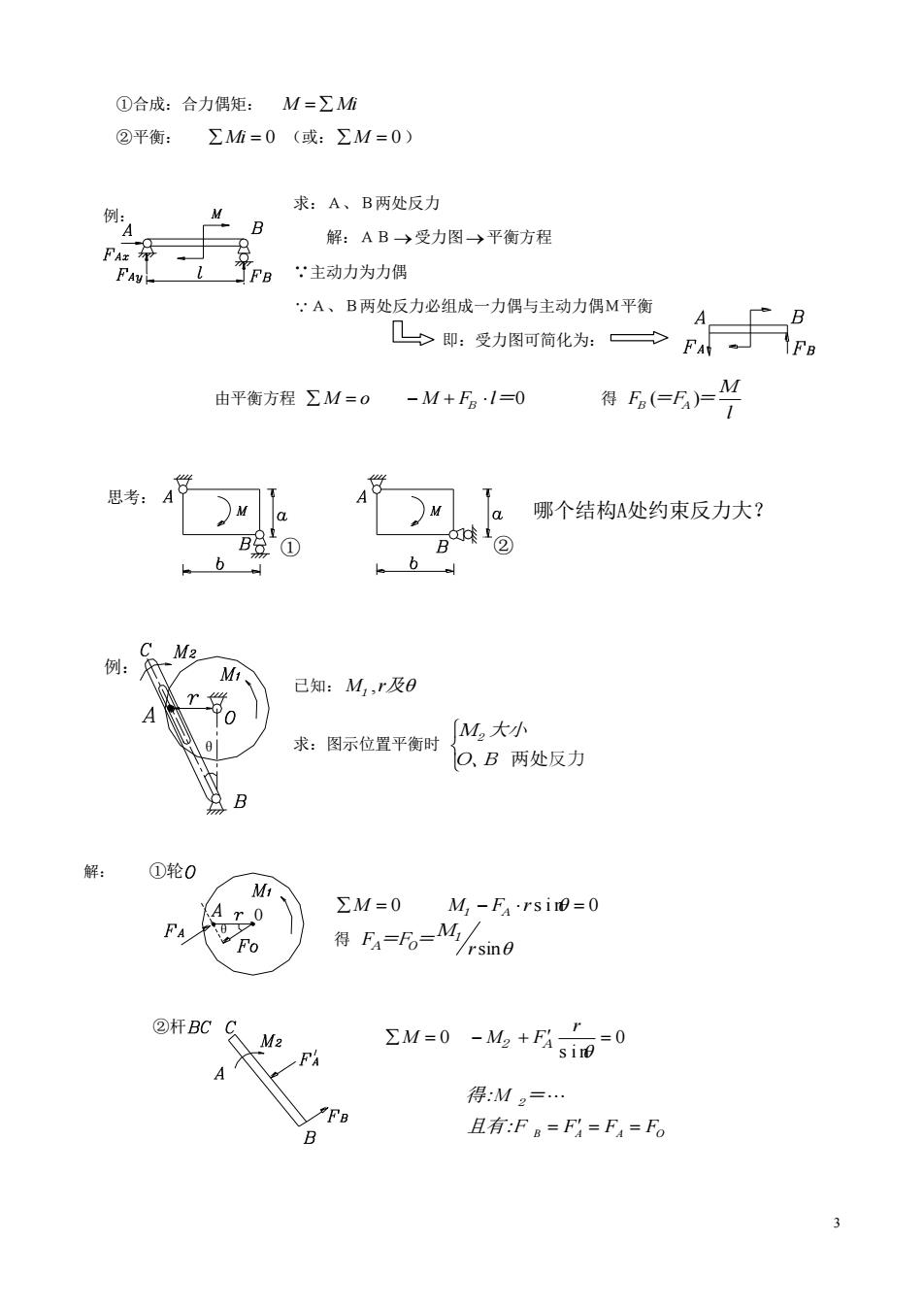
3 ②杆 ①合成:合力偶矩: M Mi ②平衡: Mi 0 (或: M 0 ) 求:A、B两处反力 解:AB 受力图 平衡方程 ∵主动力为力偶 A、B两处反力必组成一力偶与主动力偶M平衡 即:受力图可简化为: 由平衡方程 M o M FB l=0 得 l M FB (=FA )= 已知: M1 ,r及 求:图示位置平衡时 O、B 两处反力 M2 大小 解: M 0 M1 FA rsin 0 得 rsin F =F = M1 A O M 0 0 sin r M2 FA 得:M 2 = 且有:F B FA FA FO 例: ① ② 思考: 哪个结构A处约束反力大? θ 例: ①轮 O θ
求:图示位置平衡时M与P间关系。 2的6 :B (是 解:①AB ΣM=0M-FBc·a=0 得Fc=% 个M FA-A ②点C(或CDF)Pea.Cy ∑F=0P-FCB COS45°=0 得P=FcB cos45°即:M=V2Pa 思考: B ☐c 求:A、B两处反力 思考 [M2=2M M2/ 分析:图示位置平衡时,应有? M2=M★ 、M 设:图示位置平衡, 45c 且两个结构M,相同 问:哪个结构A处反力大? 哪个结构M,大? 作业:2-6,2-8b) 4
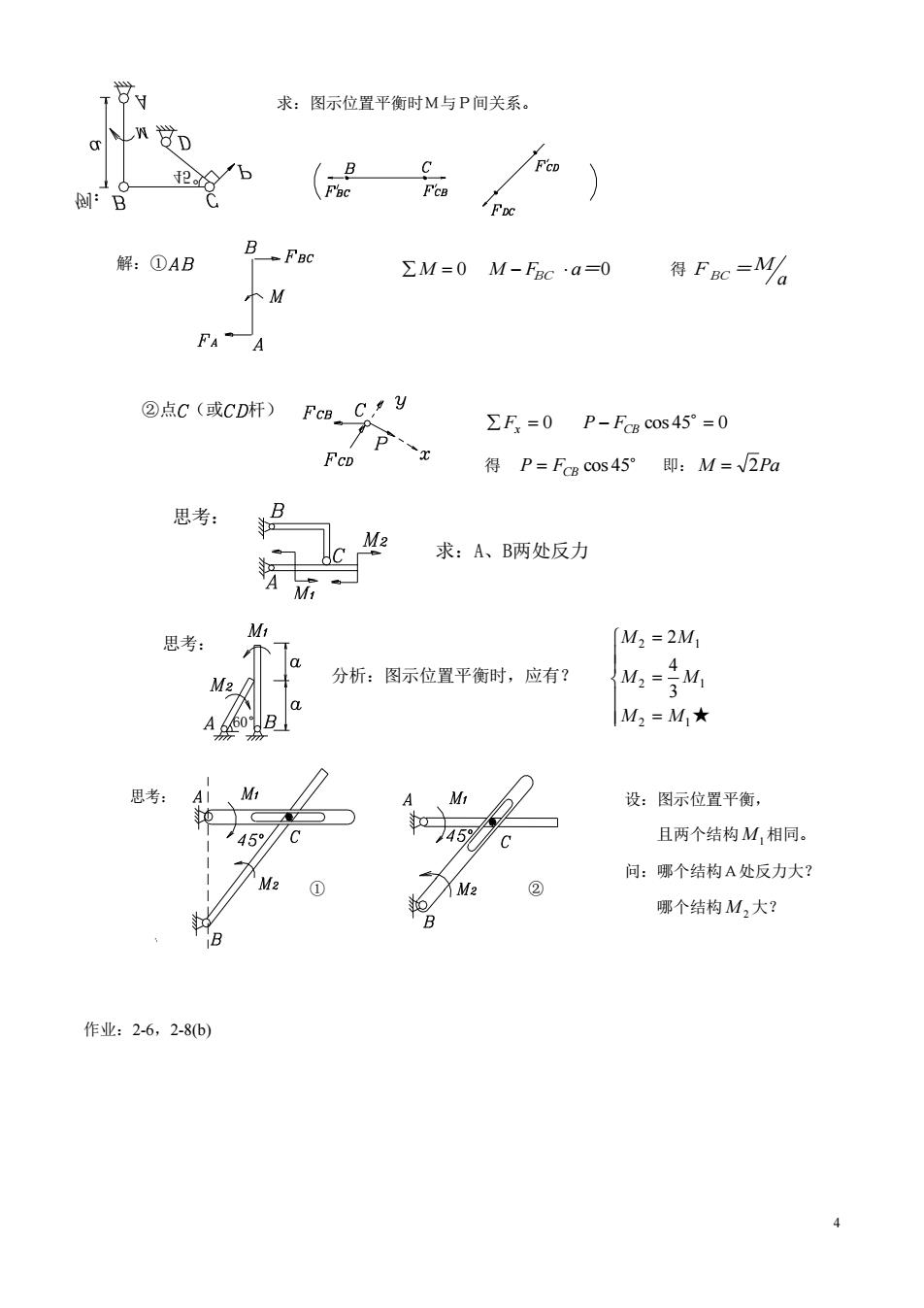
4 求:图示位置平衡时M与P间关系。 M 0 M FBC a=0 得 a F BC =M Fx 0 cos 45 0 P FCB 得 P FCB cos 45 即: M 2Pa 作业:2-6,2-8(b) 45° 例: 解:①②点 (或 杆) 思考: 求:A、B两处反力 60° 思考: 分析:图示位置平衡时,应有? 2 1★ 2 1 2 1 3 4 2 M M M M M M 设:图示位置平衡, 且两个结构 M1 相同。 问:哪个结构A处反力大? 哪个结构 M 2 大? 思考: ① ②