
(20) S11-3刚体绕定轴的转动微分方程 动量矩:L:=J0(复习要求记住的J:) 曲-zM)Uo-z)a=zM do =… 比较红=三,(何>形式相洞广义念。:转动惯量是刷体转动时损性的度量 ma=F 求:复摆(物理摆)微摆动时的运动规律 =-mgasinp(注意“±”号) d :微摆动simp0一得2+mgp=0 dt2 Jo 解为:p=sinm1+0) 。:角振幅 >由初始条件定 J。 6:初相位 周期T=2rmg0 J。 一。-Tm(可“三”次悬挂,两次求质心C,一次求TD。 4π 已知:J1、J2,主动力矩M,阻力矩M2 R ,不计摩擦, 求:轴1的角加速度a, 轮I Ra M Ja=M1-FR F=F R a 有:{1=in R2 轮Ⅱ R M, M2 J2a2=FR2-M2 M- M2 2 a2 得:a1= + (思考:若轴川大轮挂有一重物P,则应如何分析轴Ⅱ?)
1 由 ( ) e z i z M F dt dL ( ) ( ) e z Mz Fi J dt d ( ) e z M z Fi J 或 2 2 dt d J z ∵微摆动 ∴ sin 得 0 2 2 o J mga dt d sin 2 2 mga dt d J o (注意“±”号) 解为: sin( t ) J mga o o >由初始条件定 o :角振幅 :初相位 周期 2 2 4 2 T mga J mga J T o o 可利用实验求 J o 再利用平行轴定理求 c (可“三”次悬挂,两次求质心 C,一次求 T) J 得: 2 12 2 1 12 2 1 1 i J J i M M §11-3 刚体绕定轴的转动微分方程 动量矩: Lz J z (复习要求记住的 z J ) 求:复摆(物理摆)微摆动时的运动规律 已知: 1 J 、 2 J ,主动力矩 M1 ,阻力矩 M 2 又: 1 2 2 1 12 R R n n i ,不计摩擦, 求:轴I的角加速度 1 (思考:若轴Ⅱ大轮挂有一重物 P,则应如何分析轴Ⅱ?) ω Φ α 例: Φ Φ 单摆(数学摆) 分析区别 Ⅰ 例 : Ⅱ Ⅰ Ⅱ (20) 比较 ma F J z M z (F) >形式相同(广义概念), z J :转动惯量是刚体转动时惯性的度量 轮 α Ⅰ Ⅱ α 轮 有: 1 2 12 2 1 R R i Ft Ft 1 1 M1 F R1 J t 2 2 F R2 M2 J t
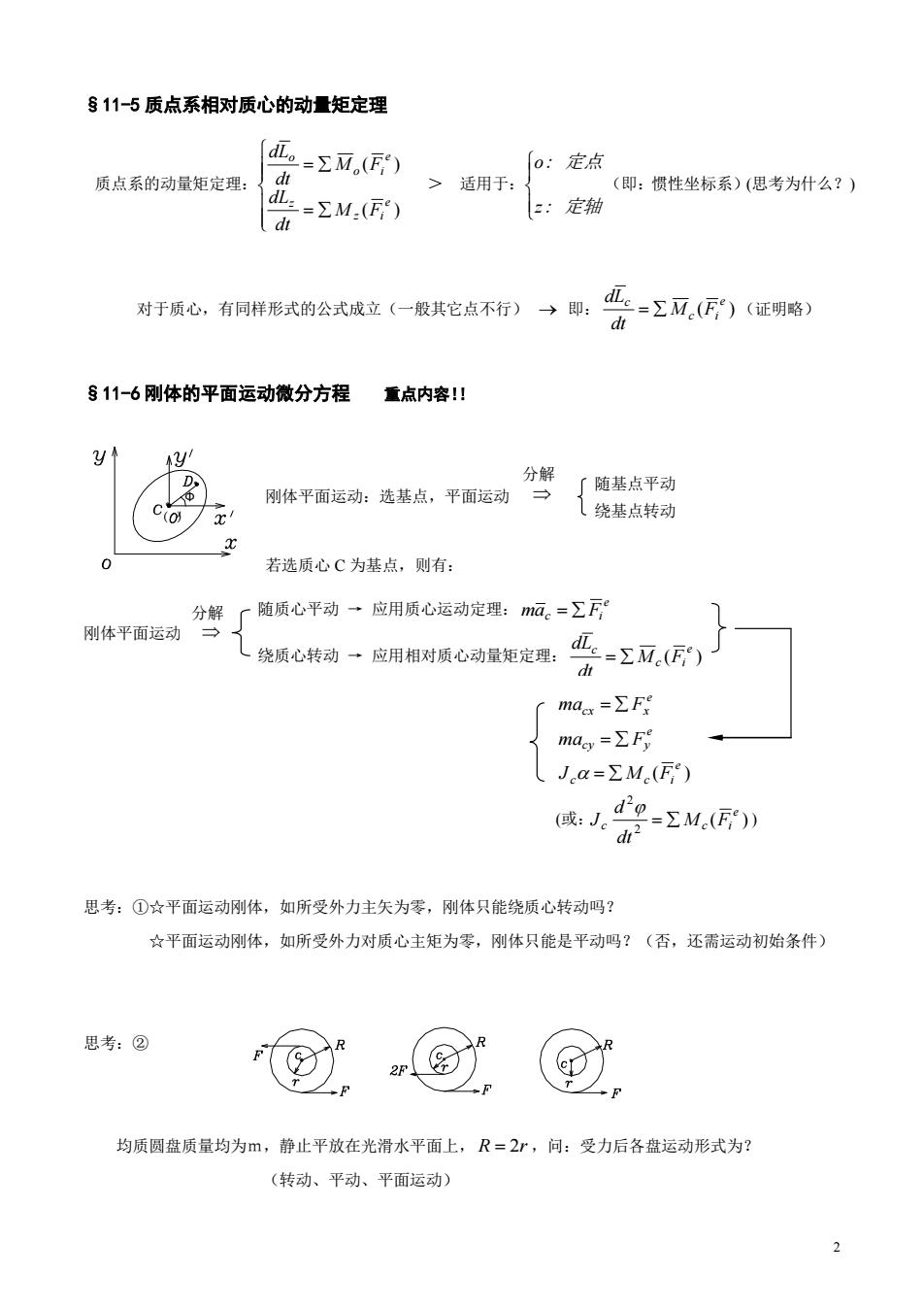
§11-5质点系相对质心的动量矩定理 质点系的动量矩定理: dL=EM.(F!) o:定点 >适用于: (即:惯性坐标系)(思考为什么?) L=ΣM:) 定轴 对于质心,有同样形式的公式成立(一般其它点不行)→即: d亚=Σ亚。()(证明略) d山 §11-6刚体的平面运动微分方程 重点内容川 y 解 刚体平面运动:选基点,平面运动→ ∫随基点平动 (绕基点转动 若选质心C为基点,则有: 用体平面运动分 C随质心平动一应用质心运动定理:ma。=∑F ,绕质心转动→应用相对质心动量矩定理: dL。 -∑M(F) maa=∑F mag=∑F CJa=∑M() 俄J49=zM》 思考:①☆平面运动刚体,如所受外力主矢为零,刚体只能绕质心转动吗? ☆平面运动刚体,如所受外力对质心主矩为零,刚体只能是平动吗?(否,还需运动初始条件) 思考:② 均质圆盘质量均为m,静止平放在光滑水平面上,R=2r,问:受力后各盘运动形式为? (转动、平动、平面运动) 2
2 §11-5 质点系相对质心的动量矩定理 §11-6 刚体的平面运动微分方程 重点内容!! 刚体平面运动:选基点,平面运动 若选质心 C 为基点,则有: 刚体平面运动 思考:①☆平面运动刚体,如所受外力主矢为零,刚体只能绕质心转动吗? ☆平面运动刚体,如所受外力对质心主矩为零,刚体只能是平动吗?(否,还需运动初始条件) 思考:② 均质圆盘质量均为m,静止平放在光滑水平面上, R 2r ,问:受力后各盘运动形式为? (转动、平动、平面运动) 分解 随基点平动 绕基点转动 Φ ( ) 质点系的动量矩定理: ( ) ( ) e z i z e o i o M F dt dL M F dt dL > 适用于: z: 定轴 o: 定点 (即:惯性坐标系)(思考为什么?) 对于质心,有同样形式的公式成立(一般其它点不行) 即: ( ) e c i c M F dt dL (证明略) 随质心平动 → 应用质心运动定理: e mac Fi 绕质心转动 → 应用相对质心动量矩定理: ( ) e c i c M F dt dL 分解 e macx Fx e macy Fy ( ) e c Mc Fi J (或: ( ) 2 2 e c Mc Fi dt d J )

例: R 均质圆轮 《纯滚动 求:1、轮心c的加速度 2、斜面的约束反力 解:轮一受力及运动分析→平面运动微分方程 x: iy: o=N-Pcos0 可得:{N 9:Ja=F.R 又有:a= 注{0、轮作纯滚动时,滑动摩擦力一般未达到最大值,(即:不能使用F=灯,且方向也可预先假定) (②、一般可忽略滚动摩阻力偶(但绝不能在纯滚动状态下忽略滑动摩擦力,否则不能纯滚动) 思考题∠ 求:益力 例:yR a 。→T已知:滚子质量m,对质心©的惯性半径为p ac 求:①ae g -C ②地面反力 N 个F纯滚动 x:ma。=T-F ae=… v:o=N-mg W=… o:Ja=Tr+FR (→即:mp2a=Tr+FR F=TP-Rr 又有:a=次及J。=mp2 p2+R2 分析F的“±”号(即:将T力向C简化后,比较p2与的大小,说明F的指向可假定》
3 例: α 纯滚动 均质圆轮 求:1、轮心c的加速度 2、斜面的约束反力 解:轮 → 受力及运动分析 平面运动微分方程 ①、轮作纯滚动时,滑动摩擦力一般未达到最大值,(即:不能使用 F Nf ,且方向也可预先假定) ②、一般可忽略滚动摩阻力偶(但绝不能在纯滚动状态下忽略滑动摩擦力,否则不能纯滚动) 已知:滚子质量m,对质心c的惯性半径为ρ 求: ① c a ②地面反力 分析 F 的“±”号(即:将 T 力向 C 简化后,比较 2 与 Rr 的大小,说明 F 的指向可假定) α θ 纯滚动 例: 注 J F R y o N P a P F g P x c c : : cos : sin 可得: F N ac . 又有: R ac 求:绳拉力 思考题 2 2 2 R Rr F T N ac J Tr FR y o N mg x ma T F c c : : : ( 即: m Tr FR 2 ) 又有: R ac 及 2 Jc m
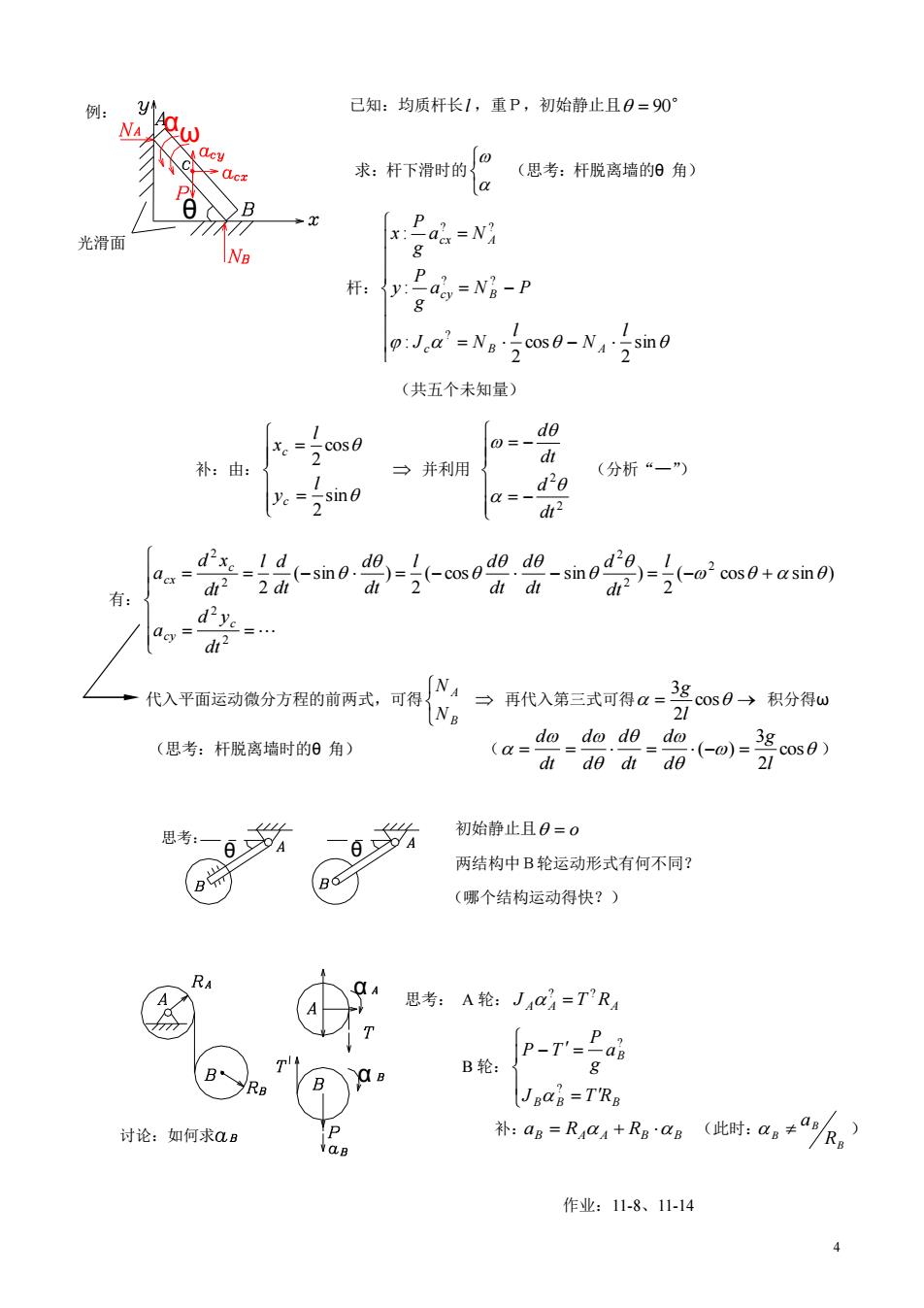
:w 已知:均质杆长1,重P,初始静止且0=90° 求:杆下滑时的 (思考:杆脱离墙的阳角) 光滑面 (x:Pai=N7 营-P o:Ja'-NaTcs0-Nsi0 (共五个未知量) 0 、 补:由: 三并利用{ d d'e (分析“一) a=-d 有:了 dt dt dt 一代入平面运动微分方程的前丙式,可得化,一再代人第三式可得a一是m0积分得心 (思考:杆脱离墙时的角) (a= d山de di de 21 思考一 初始静止且日=0 两结构中B轮运动形式有何不同? (哪个结构运动得快?) 思考:A轮:J,}=T”R T T↑ B轮: -r-go JaaB=TRB 讨论:如何求a 补:aa=Ra4+Raag(此时:a≠“,) 作业:11-8、11-14 4
4 B 轮: B B B B J T R a g P P T ? ? 补: aB RA A RB B (此时: B B B R a ) 已知:均质杆长 l ,重P,初始静止且 90 (共五个未知量) 代入平面运动微分方程的前两式,可得 B A N N 再代入第三式可得 cos 2 3 l g 积分得ω (思考:杆脱离墙时的θ 角) ( cos 2 3 ( ) l g d d dt d d d dt d ) 初始静止且 o 两结构中B轮运动形式有何不同? (哪个结构运动得快?) 思考: A 轮: A A T RA J ? ? 作业:11-8、11-14 α θ ω 例: 光滑面 θ θ 思考: α α 讨论:如何求 求:杆下滑时的 (思考:杆脱离墙的θ 角) 杆: sin 2 cos 2 : : : ? ? ? ? ? l N l J N a N P g P y a N g P x c B A c y B c x A 补:由: sin 2 cos 2 l y l x c c 并利用 2 2 dt d dt d (分析“—”) 有: 2 2 2 2 2 2 2 ( cos sin ) 2 ( cos sin ) 2 ( sin ) 2 dt d y a l dt d dt d dt l d dt d dt l d dt d x a c c y c c x