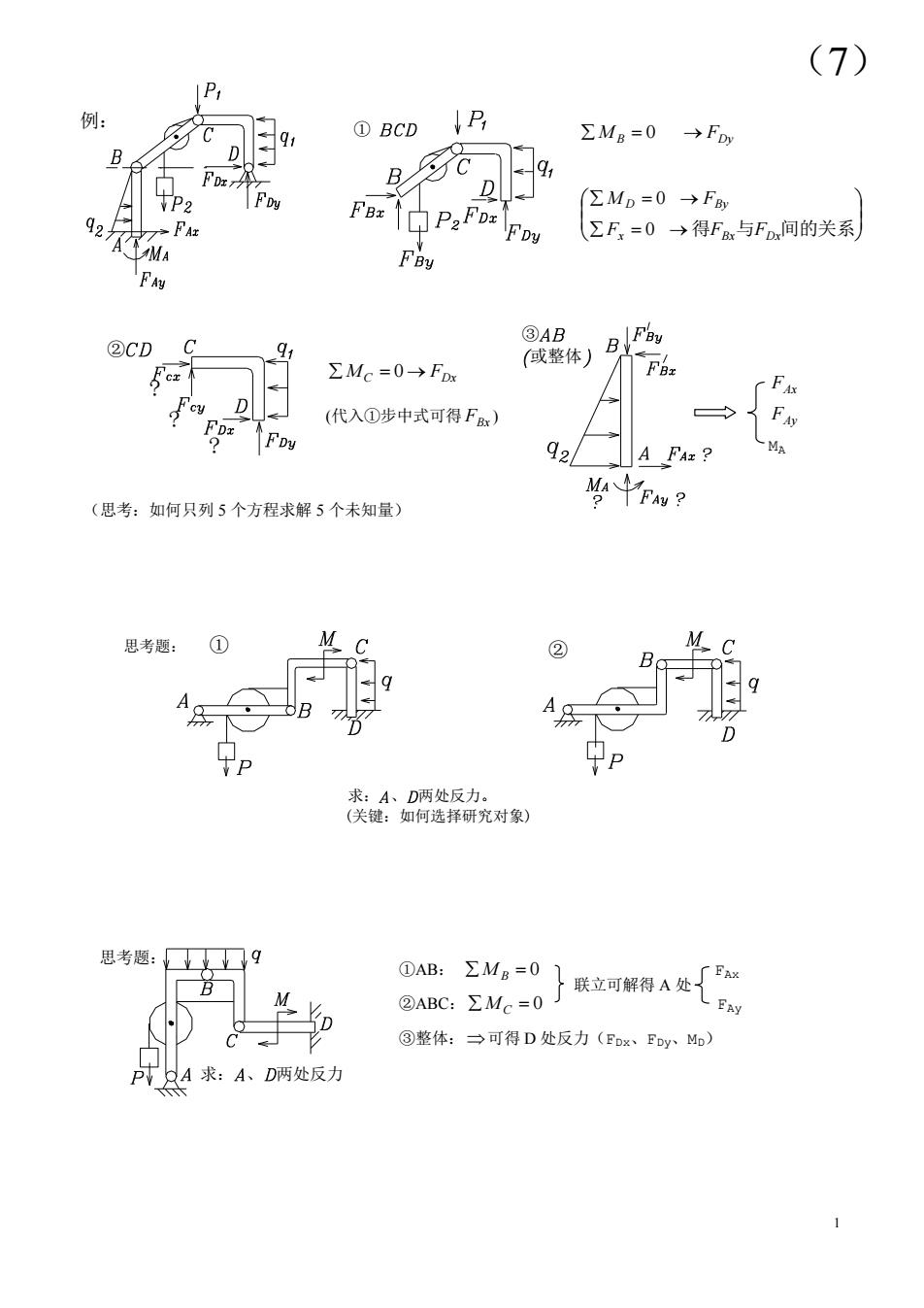
(7) 例: 2 ①BCD P ΣMB=0→FD F (∑MD=0→F A FDy ∑F=0→得Fm与Fx间的关系 MA ②CD ③AB (或整体) BFBy ∑Mc=0→F 小F D 代入①步中式可得Fx) 92/A FAz? (思考:如何只列5个方程求解5个未知量) 平pw? 思考题: ② 思考题:口9 ①AB:ΣMa=0}联立可解得A处{ ②ABC:∑Mc=0J ③整体:→可得D处反力(Ex、EyM 求:A、D两处反力
1 M B 0 FDy x 得 Bx与 Dx间的关系 D By F F F M F 0 0 MC 0 FDx (代入①步中式可得 FBx ) (思考:如何只列 5 个方程求解 5 个未知量) 求 ①AB: M B 0 FAx ②ABC: MC 0 FAy ③整体: 可得 D 处反力(FDx、FDy、MD) ? ? ? ② ③ 或整体 求: 、 两处反力。 (关键:如何选择研究对象) 思考题: ① ② 思考题: 求: 、 两处反力 例: ① (7) FAx FAy MA 联立可解得 A 处
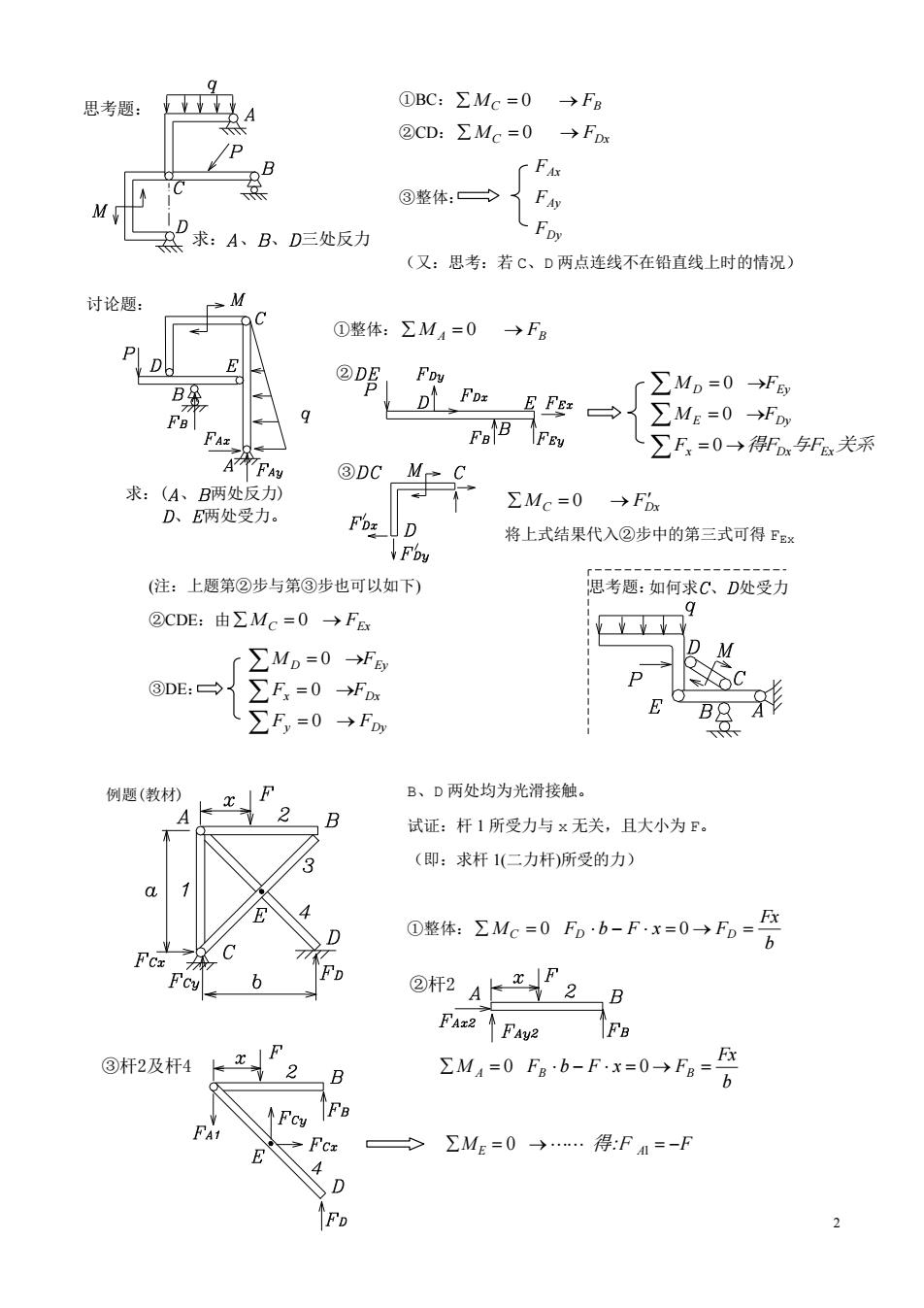
思考题: ①BC:ΣMc=0→FB ②cD:ΣMc=0→Fm C F ℃ ③整体:→ 了F M 求:A、B、D三处反力 LF四 (又:思考:若C、D两点连线不在铅直线上时的情况) 时论题: r-M ①整体:∑M=0 →FB E @唱1 ∑MD=0→f →{∑ME=0→f ∑F=0→得F.F关系 DCMC. 求:( ΣMc=0→F D、 Fo:D 将上式结果代入②步中的第三式可得E Fby (注:上题第②步与第③步也可以如下) 思考题:如何求C、D处受力 ②CDE:由∑Mc=0→Fa ∑Mp=0→f D M ③DE:→ ∑F=0→F C ∑F,=0→F 6照转 例题(教材 B、D两处均为光滑接触。 试证:杆1所受力与x无关,且大小为F。 (即:求杆1(二力杆)所受的力) ①整工M=0-F=0→= Pa2↑FAVE F阳 ③杆2及杆4 ΣM,=06-F=0-g >∑ME=0→…得:F=-F D 2
2 ③杆2及杆4 b Fx M A 0 FB b F x 0 FB ①BC: MC 0 FB ②CD: MC 0 FDx ③整体: (又:思考:若 C、D 两点连线不在铅直线上时的情况) ①整体: M A 0 FB MC FDx 0 将上式结果代入②步中的第三式可得 FEx (注:上题第②步与第③步也可以如下) ②CDE:由 MC 0 FEx ③DE: B、D 两处均为光滑接触。 试证:杆 1 所受力与 x 无关,且大小为 F。 (即:求杆 1(二力杆)所受的力) ①整体: b Fx MC 0 FD b F x 0 FD ME 0 得:F A1 F 思考题:如何求 、 处受力 思考题: 求: 、 、 三处反力 讨论题: 求:( 、 两处反力) 、 两处受力。 ③ ② FAx FAy FDy M D 0 FEy M E 0 FDy Fx 0 得FDx与FEx关系 M D 0 FEy Fx 0 FDx Fy 0 FDy 例题(教材) ②杆2

§2-6平面简单桁架的内力计算 (桁架:工程中,桥梁、建筑、起重机等常用的结构之一(对应于刚架)) 「平面桁架:各杆件在同一平面。 (节点(结点):各杆件的铰链接头。 1、杆件均为直杆 2、杆件均以铰链连接 理想桁架 3、载荷均作用在节点上,且在桁架平面内 4、杆件自重不计(或将自重分配在杆件两端节点上) 女所有杆件均为“二力杆”∫受拉 (杆件承受拉压比承受弯曲的能力大,可充分发挥构件能力。) (受压 (举例:昌平桥梁厂龙门吊车改型一例.) 静定桁架(无余杆桁架) 又:分类 超静定桁架(有余杆桁架) >各有利弊 (静不定桁架) ☒ 分析对象:“平面简单析架” (亦称:“平面理想静定桁架”) 求桁架杆件内力的常用方法厂人、节点法(应用平面汇交力系的平衡条件) 2、截面法(应用平面任意力系的平衡条件) 1、节点法:逐节点分析求解各杆件内力(平面汇交力系问题)》 例: C 求:各杆内力 「先求支座反力 解:一般{再逐节点分析求杆内力 2 P5为 FA 1、整体→ F 注:罗设各杆均为拉力。 2、逐节点分析: (由结果“士”号可知实际为拉或压杆) ①节点A F12 ②节点C ③节点D F4? D →F22 FA F3? (注:最后可利用B节点来校核计算结果) 3
3 求桁架杆件内力的常用方法 §2-6 平面简单桁架的内力计算 (桁架:工程中,桥梁、建筑、起重机等常用的结构之一(对应于刚架)) 平面桁架:各杆件在同一平面。 节点(结点):各杆件的铰链接头。 1、杆件均为直杆 2、杆件均以铰链连接 3、载荷均作用在节点上,且在桁架平面内 4、杆件自重不计(或将自重分配在杆件两端节点上) 受拉 受压 (举例:昌平桥梁厂龙门吊车改型一例。) 静定桁架(无余杆桁架) 超静定桁架(有余杆桁架) (静不定桁架) 分析对象:“平面简单桁架” (亦称:“平面理想静定桁架”) 1、节点法(应用平面汇交力系的平衡条件) 2、截面法(应用平面任意力系的平衡条件) 1、节点法:逐节点分析求解各杆件内力(平面汇交力系问题) 求:各杆内力 解:一般 1、整体 By Bx A F F F 2、逐节点分析: (注:最后可利用 B 节点来校核计算结果) 又:分类 ☆所有杆件均为“二力杆” 各有利弊 例: ? ? ②节点 ? ①节点 ③节点 ? ? 理想桁架 (杆件承受拉压比承受弯曲的能力大,可充分发挥构件能力。) 先求支座反力 再逐节点分析求杆内力 注:假设各杆均为拉力。 (由结果“±”号可知实际为拉或压杆)
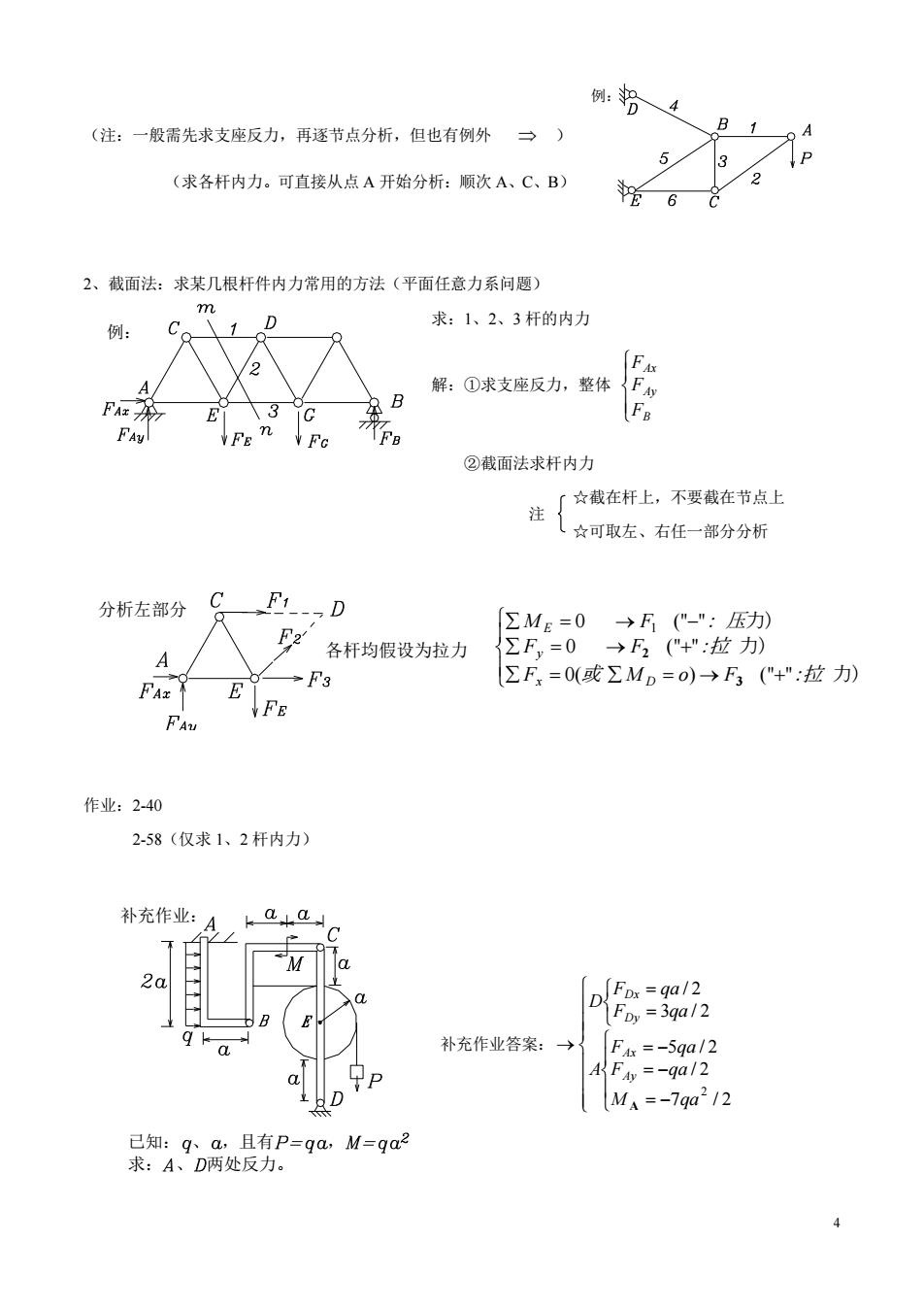
例:4 (注:一般需先求支座反力,再逐节点分析,但也有例外一) (求各杆内力。可直接从点A开始分析:顺次A、C、B) 2 6 2、截面法:求某几根杆件内力常用的方法(平面任意力系问题 例: D 求:1、2、3杆的内力 F A 解:①求支座反力,整体 F FA:2 E 3c ②截面法求杆内力 注☆酸在杆上,不要载在节点上 ☆可取左、右任一部分分析 分析左部分 C F1-,D [∑M=0→F("-":压力) 各杆均假设为拉力 ∑F,=0→F2(+":拉) FAz -F3 ∑F=0(或∑MD=o)→F3(+":拉) 作业:2-40 2-58(仅求1、2杆内力) 补充作业 2a D Fox =ga/2 补充作业答案:→ F=-5qa/2 Fw=-9a/2 .D M、=-7qa2/2 已知:g、a,且有P=ga,M=ga2 求:A、D两处反力。 4
4 (注:一般需先求支座反力,再逐节点分析,但也有例外 ) (求各杆内力。可直接从点 A 开始分析:顺次 A、C、B) 2、截面法:求某几根杆件内力常用的方法(平面任意力系问题) 求:1、2、3 杆的内力 解:①求支座反力,整体 B Ay Ax F F F ②截面法求杆内力 ☆截在杆上,不要截在节点上 ☆可取左、右任一部分分析 作业:2-40 2-58(仅求 1、2 杆内力) 补充作业答案: 7 / 2 / 2 5 / 2 3 / 2 / 2 2 M qa F qa F qa A F qa F qa D Ay Ax Dy Dx A 例: 例: 分析左部分 各杆均假设为拉力 补充作业: 已知: 、 ,且有 , 求: 、 两处反力。 注 0( ) (" " 力) 0 (" " 力) 0 (" " 力) 1 F 或 M o F :拉 F F :拉 M F : 压 x D y E 3 2