实验四弯曲、扭转组合变形的主应力和内力的电测实验 在构件受复杂载荷的情况下,测定构件某一点处的主应力大小和方向,进而进行强度分 析,是工程中经常遇到的问题。此外,测量组合变形情况下构件某处的内力分量,对于分析 和调整构件的受力大小、评价构件的受载情况、进行强度分析是非常必要的。 一、实验目的: 1,测定薄壁圆管在弯曲、扭转组合变形下外侧上、下表面指定点处的主应力大小和方 向,并和理论值进行比较 2.测定薄壁圆管在弯曲、扭转组合变形下的弯矩和扭矩,并计算他们的应力,并和理 论值进行比较: 3.进一步熟悉掌握电阻应变测量方法: 4.学习电阻应变花的应用。 二、实验设备: 1.材料力学综合试验台: 2.力、应变综合试验仪。 三、实验原理及方法: 1.确定一点主应力的大小和方向 本实验利用应变片在电桥上的不同联接方法来测取构件在组合变形时的内力。实验是在 一端固定,一端自由的悬臂曲拐结构上进行,实验段的横截面为空心铝圆轴,其外径为D, 内径为d。在曲拐的自由端施加力F,使得在圆轴上产生扭转和弯曲变形。结构如图4.1所 /45 图4.1薄壁圆筒受力图 图42贴片方位 在弯曲、扭转组合变形情况下,圆管的某一截面的上表面m点和下表面m点处于二向 应力状态,存在由弯矩引起的弯曲正应力和由扭转引起的扭转切应力,且主应力方向未知 为了测出主应力和主方向, 在测点 m、m分别贴上45应变花,即:在沿与轴线成45 的方向各贴一片应变片,沿轴线方向上贴一片。上下共六片。贴片方位如图4.2所示。 由材料力学可知,任意方向上的线应变与沿X、y方向的线应变x、、切应变Y 的关系为:
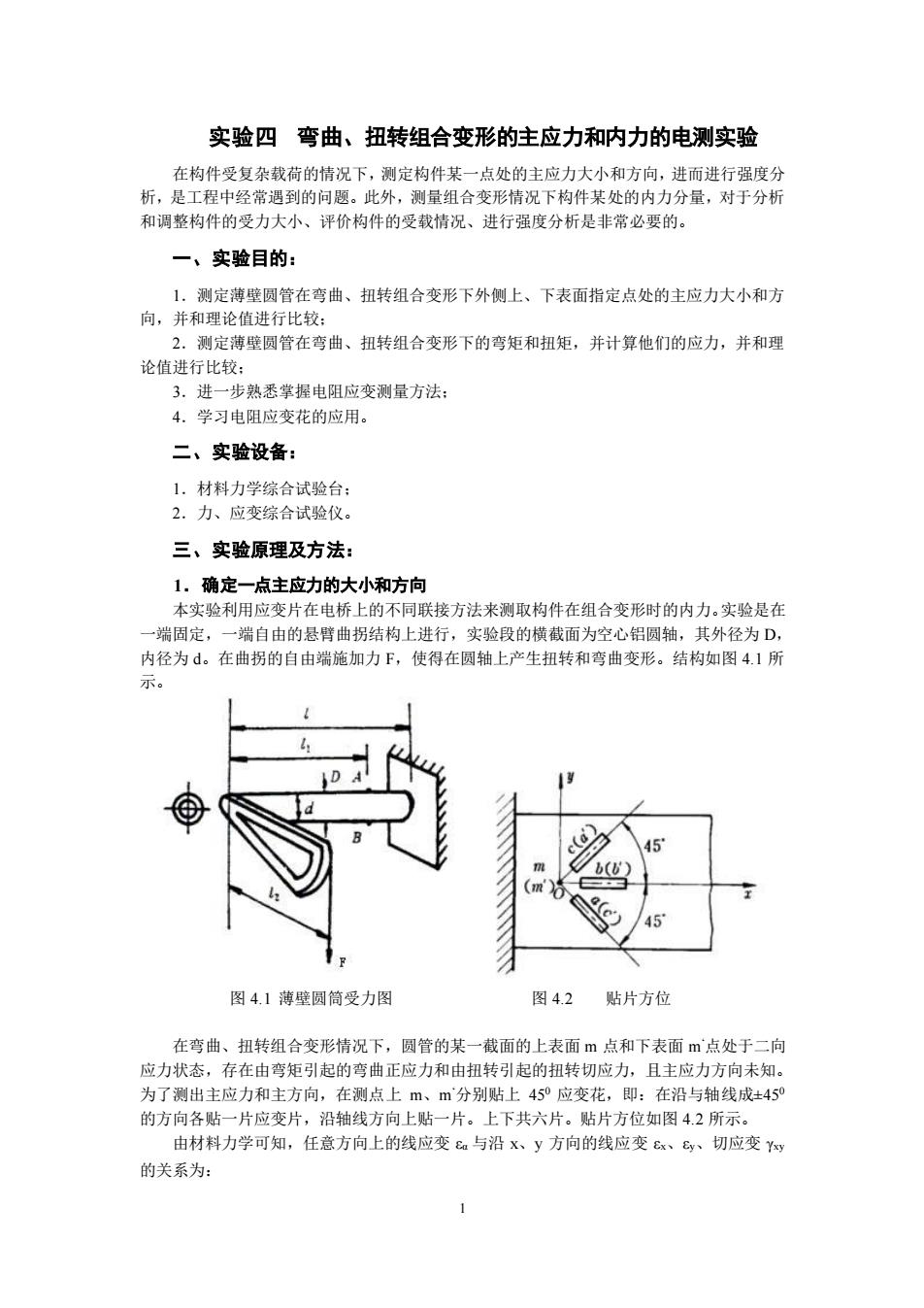
1 实验四 弯曲、扭转组合变形的主应力和内力的电测实验 在构件受复杂载荷的情况下,测定构件某一点处的主应力大小和方向,进而进行强度分 析,是工程中经常遇到的问题。此外,测量组合变形情况下构件某处的内力分量,对于分析 和调整构件的受力大小、评价构件的受载情况、进行强度分析是非常必要的。 一、实验目的: 1.测定薄壁圆管在弯曲、扭转组合变形下外侧上、下表面指定点处的主应力大小和方 向,并和理论值进行比较; 2.测定薄壁圆管在弯曲、扭转组合变形下的弯矩和扭矩,并计算他们的应力,并和理 论值进行比较; 3.进一步熟悉掌握电阻应变测量方法; 4.学习电阻应变花的应用。 二、实验设备: 1.材料力学综合试验台; 2.力、应变综合试验仪。 三、实验原理及方法: 1.确定一点主应力的大小和方向 本实验利用应变片在电桥上的不同联接方法来测取构件在组合变形时的内力。实验是在 一端固定,一端自由的悬臂曲拐结构上进行,实验段的横截面为空心铝圆轴,其外径为 D, 内径为 d。在曲拐的自由端施加力 F,使得在圆轴上产生扭转和弯曲变形。结构如图 4.1 所 示。 图 4.1 薄壁圆筒受力图 图 4.2 贴片方位 在弯曲、扭转组合变形情况下,圆管的某一截面的上表面 m 点和下表面 m‘点处于二向 应力状态,存在由弯矩引起的弯曲正应力和由扭转引起的扭转切应力,且主应力方向未知。 为了测出主应力和主方向,在测点上 m、m‘分别贴上 450 应变花,即:在沿与轴线成±450 的方向各贴一片应变片,沿轴线方向上贴一片。上下共六片。贴片方位如图 4.2 所示。 由材料力学可知,任意方向上的线应变 εα 与沿 x、y 方向的线应变 εx、εy、切应变 γxy 的关系为:

6,-6+cs2a-gm20 (4.1) 随a的变化而变化,主应变由下式计算: 5.55±G,-,广+7。 (4.2 2 两个互相垂直的主方向由下式确定: am2a,=6,-8 Y (4.3) 对各向同性的线弹性材料,主应力1、02和主应变、方向一致,并可由广义胡克 定律求出: o=1-G+,) (4.4) 实测时,三枚应变片的a角分别为-45、450、0°代入式(4.1),得出沿这三个方向的线 应变分别是: 2 6=6 (4.5) 6=5+8.n 22 从以上三式中解出: Ex=E0 ,=646+845-80 (4.6) yg=645-645 由于6。、4s、es可以直接测定,所以、和可由测量的结果求出。将它们代入 主应变计算公式4.2,得: 怎-±9w-r6- (4.7) 2 同时确定主应变方向为: 645-65 an2a=-26,-66-65 (4.8) 由上式解出相差π2的两个,确定两个相互垂直的主方向。若x的代数值大于, ·注:由于圆轴表面一点处于平面应力状态,将此平面内的两个主应力和主应变分别称为G、0?、6, 6,这并不代表三向应力状态下的主应力和主应变,下同。 2
2 cos 2 sin 2 2 2 2 x y x y xy + − = + − (4.1) εα随 α 的变化而变化,主应变由下式计算: 1 2 2 2 1 ± ( ) 2 2 x y x y xy + = − + (4.2) 两个互相垂直的主方向 α0 由下式确定: 0 tan 2 xy x y = − − (4.3) 对各向同性的线弹性材料,主应力 σ1、σ2 和主应变 ε1、ε2 方向一致,并可由广义胡克 定律求出1: 1 1 2 2 2 2 1 2 ( ) 1 ( ) 1 E E = + − = + − (4.4) 实测时,三枚应变片的 α 角分别为-450、450、0 0 代入式(4.1),得出沿这三个方向的线 应变分别是: 45 0 45 2 2 2 2 x y xy x x y xy − + = + = + = − (4.5) 从以上三式中解出: 0 45 45 0 45 45 x y xy − − = = + − = − (4.6) 由于 0 、ε45、ε-45 可以直接测定,所以 εx、εy 和 γxy 可由测量的结果求出。将它们代入 主应变计算公式 4.2,得: 1 45 45 2 2 45 0 45 0 2 2 ( ) ( ) 2 2 − − + = − + − (4.7) 同时确定主应变方向为: 45 45 0 0 45 45 tan 2 2 − − − = − − − (4.8) 由上式解出相差 π/2 的两个 α0,确定两个相互垂直的主方向。若 εx 的代数值大于 εy, 1 注:由于圆轴表面一点处于平面应力状态,将此平面内的两个主应力和主应变分别称为 1 、 2 、 1 、 2 ,这并不代表三向应力状态下的主应力和主应变,下同

则由x轴量起,绝对值较小的确定为主应变8(对应于o)的方向,反之,若〈马, 则由x轴量起,绝对值较小确定为主应变6,(对应于),的方向。 将主应变代入广义胡克定律,便可得到m点的主应力: G1_E(E5+84s± G,2-20s-》+(65-6) (4.9) 如果测得三个方向的应变值e45、e45、0,由式(4.8入、(4.9)即可确定该点处主应力的 大小和方向。 2.测定弯矩和弯曲正应力: 在圆周的下表面与m相对的m上,粘贴一枚与m点相同的应变花,其三枚应变片分别 为0°、45、450,相对位置如图4.2。圆管虽为弯扭组合变形,但m和m两点沿x方向只 有因弯曲引起的拉伸和压缩应变,且两者数值相等符号相反.因此,将m点0应变片与m点 的0°应变片接成半桥得: 6,=(6+6,)-(-6+6)=26 (4.10 其中:6一m点因弯曲引起的应变(6: 67 一温度引起的应变: 6,—仪器的读数: 因此可求得最大弯曲正应力为: a=bE (4.11) 2 截面上最大弯曲应力计算公式为 s MD 32D 21π(D-d (4.12) 令以上两式相等,即可得到弯矩为: M=Ex() 64D (4.13)
3 则由 x 轴量起,绝对值较小的 α0 确定为主应变 1 (对应于 σ1)的方向,反之,若 εx﹤εy, 则由 x 轴量起,绝对值较小 α0 确定为主应变 2 (对应于 σ2),的方向。 将主应变代入广义胡克定律,便可得到 m 点的主应力: 1 45 45 2 2 45 0 45 0 2 ( ) 2 ( ) ( ) 2(1 ) 2(1 ) E E − − + = − + − − + (4.9) 如果测得三个方向的应变值 ε45、ε-45、ε0,由式(4.8)、(4.9)即可确定该点处主应力的 大小和方向。 2.测定弯矩和弯曲正应力: 在圆周的下表面与 m 相对的 m‘上,粘贴一枚与 m 点相同的应变花,其三枚应变片分别 为 0 0’、450‘、-450’,相对位置如图 4.2。圆管虽为弯扭组合变形,但 m 和 m‘两点沿 x 方向只 有因弯曲引起的拉伸和压缩应变,且两者数值相等符号相反。因此,将 m 点 0 0 应变片与 m‘点 的 0 0 应变片接成半桥得: ( ) ( ) 2 r b T b T b = + − − + = (4.10) 其中: b ——m 点因弯曲引起的应变( 0 ); T ——温度引起的应变; r ——仪器的读数; 因此可求得最大弯曲正应力为: 2 E r = (4.11) 截面上最大弯曲应力计算公式为 4 4 32 2 ( ) MD MD I D d = = − (4.12) 令以上两式相等,即可得到弯矩为: 4 4 ( ) 64 r E D d M D − = (4.13)

3。测定扭矩和扭转切应力: 当圆管受纯扭转时,m点的应变片a和c与m点的应变片a和c都沿着主应力方向变 形,又因为主应力。1和。?大小相等符号相反,故四枚应变片的应变的绝对值相等,而且无 与a同号,与、异号。将四枚应变片接成全桥,则: 6,=6。-6.+6。-6=6-(-6)+6-(-6)=46,(4.14) 6-5 —扭转时的主应变,将它代入广义胡克定律得: E E E 40+ (4.15) 又因为扭转时主应力01和t相等,故有: 01=r21p 16TD (4.16) 0 由以上两式求得扭矩为: E,z(D-d) T=4+m16D (4.17) 通过接线,弯曲的影响将相互抵消。 四、实验步骤: 1.设计好本实验所需的各类数据表格: 2.测量试样尺寸D、d小、4、马2: 3.主应力大小、方向的确定:将薄壁圆筒上的工作应变片按不同测试要求接入到力、 应变综合实验仪上的A、B端,公共补偿片接入到桥路选择的补偿位置上,进行外补偿半桥 单臂测量: 4.按下仪器面板上的自动平衡,此时显示面板上的6个液晶屏幕均显示为零,如果一 次不能显示为零,请反复多次按压,直至全部显示为零,此仪器只能显示6个应变值,如果 多于6个,请按下通道切换键: 5.做第一个内容,一点的应力状态,将6个应变片分别接于应变仪上,补偿片接于桥 路选择的补偿位置上,拧紧所有螺丝,开始实验。逆时针摇动手柄缓慢加载,用均匀漫速加 载至初载荷Fo=10ON: 6.实验采用一次性加载方式,终极载荷为F=80ON,载荷加到8OON之后,读取每个点 的应变读数并记录下来,在这儿别忘了将每根线的颜色和读数做记录,否则将无法带入公式 进行计算, 7.卸载,并重复5、6步骤,每项实验至少重复三次: 8.测定弯矩M,取m和m两点的纵向应变片b和b,用相互补偿的半桥接线方法测 定截面上的弯矩M:此时将桥路选择的接线应放在半桥的位置上: 9.测定扭矩T,首先将桥路选择的接线应放在全桥的位置上,将a、c、a、c四枚应变 4
4 3.测定扭矩和扭转切应力: 当圆管受纯扭转时,m 点的应变片 a 和 c 与 m‘点的应变片 a ‘和 c ‘都沿着主应力方向变 形,又因为主应力 1 和 2 大小相等符号相反,故四枚应变片的应变的绝对值相等,而且 εa 与 εa‘同号,与 εc、εc’异号。将四枚应变片接成全桥,则: ' ' 1 1 1 1 1 ( ) ( ) 4 r a c a c = − + − = − − + − − = (4.14) 1 4 r = ε1——扭转时的主应变,将它代入广义胡克定律得: 1 2 2 1 2 1 1 2 ( ) [ ( )] 1 1 4(1 ) r E E E = + = + − = − − + (4.15) 又因为扭转时主应力 1 和 τ 相等,故有: 1 4 4 2 16 2 ( ) p TD TD I D d = = = − (4.16) 由以上两式求得扭矩为: 4 4 ( ) 4(1 ) 16 E r D d T D − = + (4.17) 通过接线,弯曲的影响将相互抵消。 四、实验步骤: 1.设计好本实验所需的各类数据表格; 2.测量试样尺寸 D、d、 1 l 、 2 l ; 3.主应力大小、方向的确定:将薄壁圆筒上的工作应变片按不同测试要求接入到力、 应变综合实验仪上的 A、B 端,公共补偿片接入到桥路选择的补偿位置上,进行外补偿半桥 单臂测量; 4.按下仪器面板上的自动平衡,此时显示面板上的 6 个液晶屏幕均显示为零,如果一 次不能显示为零,请反复多次按压,直至全部显示为零,此仪器只能显示 6 个应变值,如果 多于 6 个,请按下通道切换键; 5.做第一个内容,一点的应力状态,将 6 个应变片分别接于应变仪上,补偿片接于桥 路选择的补偿位置上,拧紧所有螺丝,开始实验。逆时针摇动手柄缓慢加载,用均匀漫速加 载至初载荷 F0=100N; 6.实验采用一次性加载方式,终极载荷为 F=800N,载荷加到 800N 之后,读取每个点 的应变读数并记录下来,在这儿别忘了将每根线的颜色和读数做记录,否则将无法带入公式 进行计算, 7.卸载,并重复 5、6 步骤,每项实验至少重复三次; 8.测定弯矩 M,取 m 和 m‘两点的纵向应变片 b 和 b ’,用相互补偿的半桥接线方法测 定截面上的弯矩 M;此时将桥路选择的接线应放在半桥的位置上; 9.测定扭矩 T,首先将桥路选择的接线应放在全桥的位置上,将 a、c、a ‘、c ‘四枚应变

片接成全桥,同样是分级等增量加载(分3级),每增加一级载荷,依次记录各点应变片的 应变读数,直至最终载荷。每项实验至少重复三遍: 0.完成全部实验内容后,卸除载荷,关闭电源拆线整理所用仪器设备,清理现场,将 所用仪器设备复原。数据经教师检查签字。 注意事项: 1.实验装置中,圆筒的管壁很薄,为避免损坏装置,注意切勿超载,不能用力扳动圆筒的自由端 和力臂, 2.拆线时注意拆线时动作要轻,以免叉子掉下来(如果叉子己掉下,及时通知老师焊上): 3.全桥接线时注意正、负的相应位置,以免测出数据不准确。 五、实验数据处理: 1.理论计算 弯矩、扭矩和主应力理论值计算公式分别为: M=Fxh T=Fxh W=I 20-a o,2mM±VP+7) 01_1 式中:加-受0-a)是空心调台的数有数面系敌其中,口=% 2.实验计算 1计算主应变、主方向、弯矩、扭矩时,要用同载荷、同位置的平均值进行计算:用 次同一点测得的值计算平均值: 2.误差计算,计算各点相对误差 6=-0生x100% 0 3.比较各测点的理论与实验的差值,简要分析产生误差的原因:
5 片接成全桥,同样是分级等增量加载(分 3 级),每增加一级载荷,依次记录各点应变片的 应变读数,直至最终载荷。每项实验至少重复三遍; 10.完成全部实验内容后,卸除载荷,关闭电源拆线整理所用仪器设备,清理现场,将 所用仪器设备复原。数据经教师检查签字。 注意事项: 1.实验装置中,圆筒的管壁很薄,为避免损坏装置,注意切勿超载,不能用力扳动圆筒的自由端 和力臂; 2.拆线时注意拆线时动作要轻,以免叉子掉下来(如果叉子已掉下,及时通知老师焊上); 3.全桥接线时注意正、负的相应位置,以免测出数据不准确。 五、实验数据处理: 1.理论计算; 弯矩、扭矩和主应力理论值计算公式分别为: M F l = 1 T F l = 2 3 4 (1 ) 32 D W = − 1 2 2 2 1 ( ) 2 M M T W = + 式中: 3 4 (1 ) 32 D W = − 是空心圆管的抗弯截面系数,其中, d D = 。 2.实验计算 1.计算主应变、主方向、弯矩、扭矩时,要用同载荷、同位置的.平均值进行计算;用三 次同一点测得的值计算平均值; 2.误差计算,计算各点相对误差 100% − = 理 实 理 3.比较各测点的理论与实验的差值,简要分析产生误差的原因;

六、预习及思考题: 1.预习本节内容和材料力学中关于应力状态分析和应变状态分析的内容: 2.主应力测量中,应变花是否可沿任意方向粘贴? 3.测弯矩时,这里用两枚0度片组成相互补偿电路,也可只用一枚纵向片和补偿电路 两种方法何者为好? 6
6 六、预习及思考题: 1.预习本节内容和材料力学中关于应力状态分析和应变状态分析的内容; 2.主应力测量中,应变花是否可沿任意方向粘贴? 3.测弯矩时,这里用两枚 0 度片组成相互补偿电路,也可只用一枚纵向片和补偿电路 两种方法何者为好?