北京化工大学：《材料力学》课程教学课件（PPT讲稿）第十三章 能量方法

U K 第十三章能量方法 本章内容： 1概述 2杆件变形能的计算 3变形能的普遍表达式 4互等定理 5卡氏定理 6虚功原理 7单位载荷法莫尔积分 8计算莫尔积分的图乘法

2 第十三章 能量方法 本章内容: 1 概述 2 杆件变形能的计算 3 变形能的普遍表达式 4 互等定理 5 卡氏定理 6 虚功原理 7 单位载荷法 莫尔积分 8 计算莫尔积分的图乘法

U K §13.1概述 能量原理 与功和能有关的定理，统称为能量原理。 运用能量原理求解问题的方法称为能量法。 功能原理 外力的功等于变形能： U=W §13.2杆件变形能的计算 1轴向拉伸或压缩 F21 U=W= 2 2EA

3 §13. 1 概述 能量原理 与功和能有关的定理，统称为能量原理。 运用能量原理求解问题的方法称为能量法。 功能原理 外力的功等于变形能: U =W §13. 2 杆件变形能的计算 1 轴向拉伸或压缩 U =W= Fl 2 1 EA F l 2 2 = F l  l

U K §13.2杆件变形能的计算 1轴向拉伸或压缩 U-W--FAl= F21 2 2EA 轴力F,是x的函数时 dU= F(x)dx F 2EA 2EA 应变能密 1=-O8= 度 2 2E

4 §13. 2 杆件变形能的计算 1 轴向拉伸或压缩 U =W= Fl 2 1 EA F l 2 2 = 轴力 是x的函数时 EA F x x U N 2 ( )d d 2 =  = l N EA F x x U 2 ( )d 2 应变能密 度  2 1 u = 2E 2  = F l  l FN

U K U= )dx 2EA 1 应变能密度 u= 2 2E 2纯剪切 应变能密度 u -TY 2 3扭转 U=w=m= m21 2 2GI, 0中-B 扭转杆的扭矩m与扭转角中的关系曲线

5  = l N EA F x x U 2( ) d 2 应变能密度  21 u = 2 E2  = 2 纯剪切  21 u = 2 G2  应变能密度 = 3 扭转 U = W m 21 = GI p m l 2 2 =

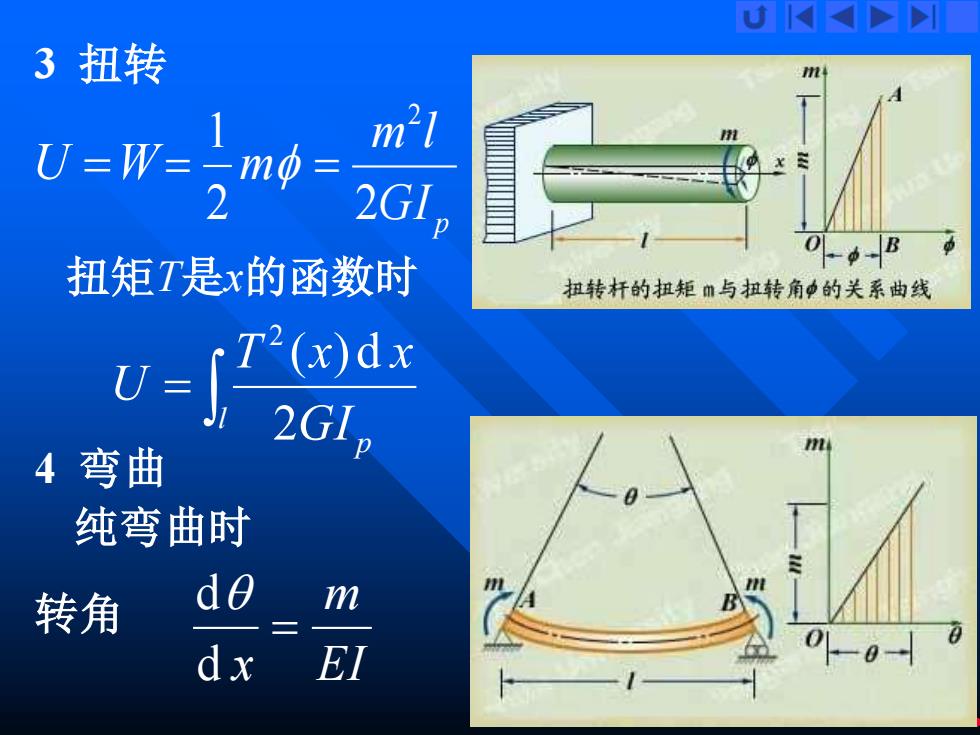
U K 3扭转 C=W-m-2 m21 2 GI, 扭矩T是x的函数时 扭转杆的扭矩m与扭转角中的关系曲线 2GIp 4弯曲 纯弯曲时 转角 do m dx EI 0-0-

6 3 扭转 U =W m 2 1 = GI p m l 2 2 = 扭矩T是x的函数时  = l GI p T x x U 2 ( )d 2 4 弯曲 纯弯曲时 转角 EI m x = d d

U K 4弯曲 纯弯曲时 转角 d m dx EI -0- m d0= dx EI 纯弯曲时各截面的弯矩相等，m为常数。 → - -dx ml EI 变形能 U=W=三m0 m21 2E1

7 4 弯曲 纯弯曲时 转角 EI m x = d d x EI m d = d 纯弯曲时各截面的弯矩相等，m为常数。  = l x EI m 0  d EI ml  = 变形能 U =W m 2 1 = EI m l 2 2 =

U K 0=a ml 0 EI 变形能 m27 U=W=二m0 2 2E1 横力弯曲时 对细长梁，剪力引起的变形能与弯矩引起的变 形能相比很小，通常可忽略不计。 横力弯曲时，弯矩是x的函数。 dU= M2(x)dx 2E1 U=∫ M2(x)dx 2EI

8  = l x EI m 0  d EI ml  = 变形能 U =W m 2 1 = EI m l 2 2 = 横力弯曲时 对细长梁，剪力引起的变形能与弯矩引起的变 形能相比很小，通常可忽略不计。 横力弯曲时，弯矩是x的函数。 EI M x x U 2 ( )d d 2 =  = l EI M x x U 2 ( )d 2

U K dU= M2(x)dx M2(x)dx 2EI U- 2E1 5用广义力和广义位移表示变形能 可将 U-FN,-mo.-mo 统一写为 9

9 EI M x x U 2 ( )d d 2 =  = l EI M x x U 2 ( )d 2 5 用广义力和广义位移表示变形能 U =W F 2 1 = , 2 1 可将 U = Fl 统一写为 , 2 1 U = m U m 2 1 =

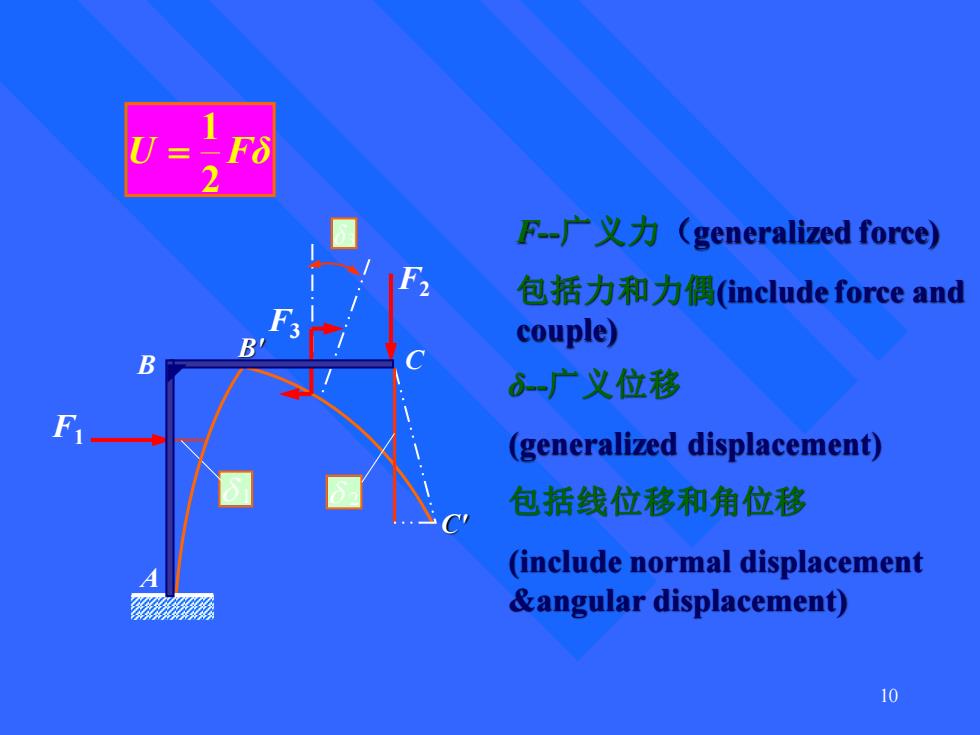
F-广义力(generalized force) 包括力和力偶(include force and couple) B 6广义位移 (generalized displacement) 包括线位移和角位移 (include normal displacement &angular displacement) 10

10 F--广义力 （generalized force) 包括力和力偶(include force and couple) δ--广义位移 (generalized displacement) 包括线位移和角位移 (include normal displacement &angular displacement)  1  2  3 B ' C ' U Fδ 21 = F3 B CF2 A F1

例1试求图示悬臂梁的变形能，并利用功能原理求自由端B的 挠度。 解： M(=-F -a骨 W=F.VB 由U=W得 VB 3EI

11 例1 试求图示悬臂梁的变形能，并利用功能原理求自由端B的 挠度. A B F l x 解： M(x) = −F  x EI F l x EI Fx x EI M x U l l 6 d 2 ( ) d 2 ( ) 2 3 0 2 2 = = =   B 2 1 W = F  v 由U=W 得 EI Fl v 3 3 B =