
第7章土的抗剪强度 第1节概述 土的抗剪强度 土体在外力作用和自重荷载下必然产生(剪)切应力和剪切变形, 当剪应力达到士体的极限抵抗力时必然发生剪切破坏,而土体抵抗剪 切破坏的极限能力就是土的抗剪强度。 工程实践中强度破坏多数都与土的抗剪强度有关。 (a) (6) (c) 与强度破坏有关的工程问题 (a)边坡稳定 (b)挡土墙土压力 (c)地基承载力 土质学与土力学 42-1 吉林大学建设工程学院
土质学与土力学 42—1 吉林大学建设工程学院 土的抗剪强度 土体在外力作用和自重荷载下必然产生(剪)切应力和剪切变形, 当剪应力达到土体的极限抵抗力时必然发生剪切破坏,而土体抵抗剪 切破坏的极限能力就是土的抗剪强度。 第1节 概述 与强度破坏有关的工程问题 工程实践中强度破坏多数都与土的抗剪强度有关。 (a)边坡稳定 (b)挡土墙土压力 (c)地基承载力
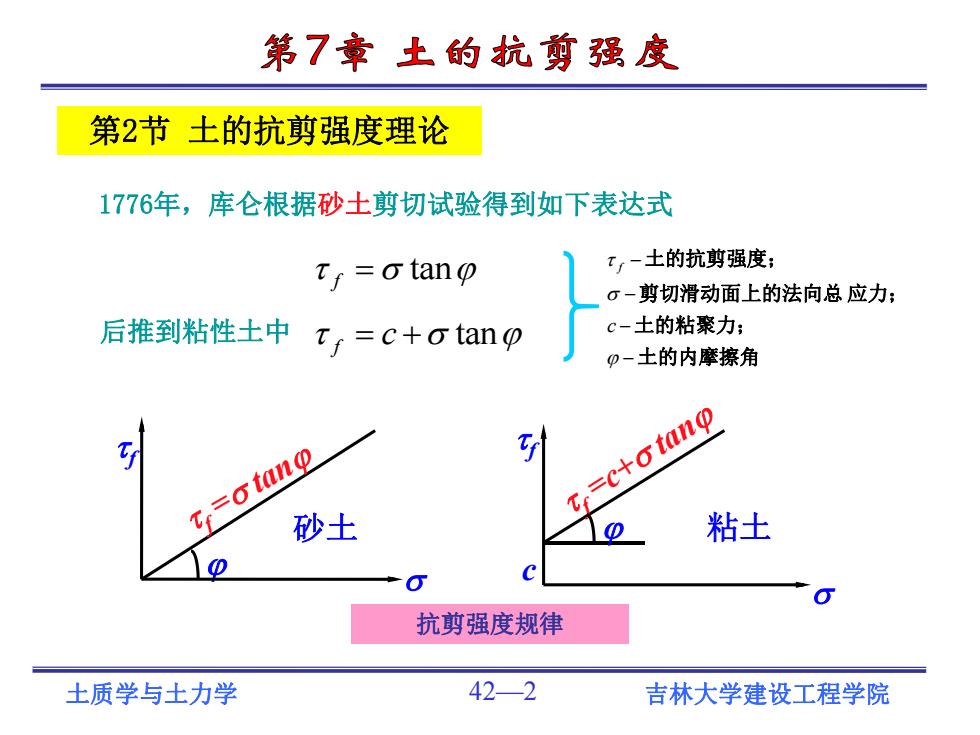
第7章土的抗剪强度 第2节土的抗剪强度理论 1776年,库仑根据砂土剪切试验得到如下表达式 tr =o tang t,-土的抗剪强度; 6-剪切滑动面上的法向总应力; 后推到粘性土中tf=C+otanp c-土的粘聚力; p-土的内摩擦角 T=otang T=c+otanp 砂土 粘土 抗剪强度规律 土质学与土力学 42-2 吉林大学建设工程学院
土质学与土力学 42—2 吉林大学建设工程学院 f =c+ tan 粘土 c f f = tan 砂土 f 1776年,库仑根据砂土剪切试验得到如下表达式 第2节 土的抗剪强度理论 抗剪强度规律 f tan 后推到粘性土中 f c tan 土的内摩擦角 土的粘聚力; 剪切滑动面上的法向总 应力; 土的抗剪强度; c f
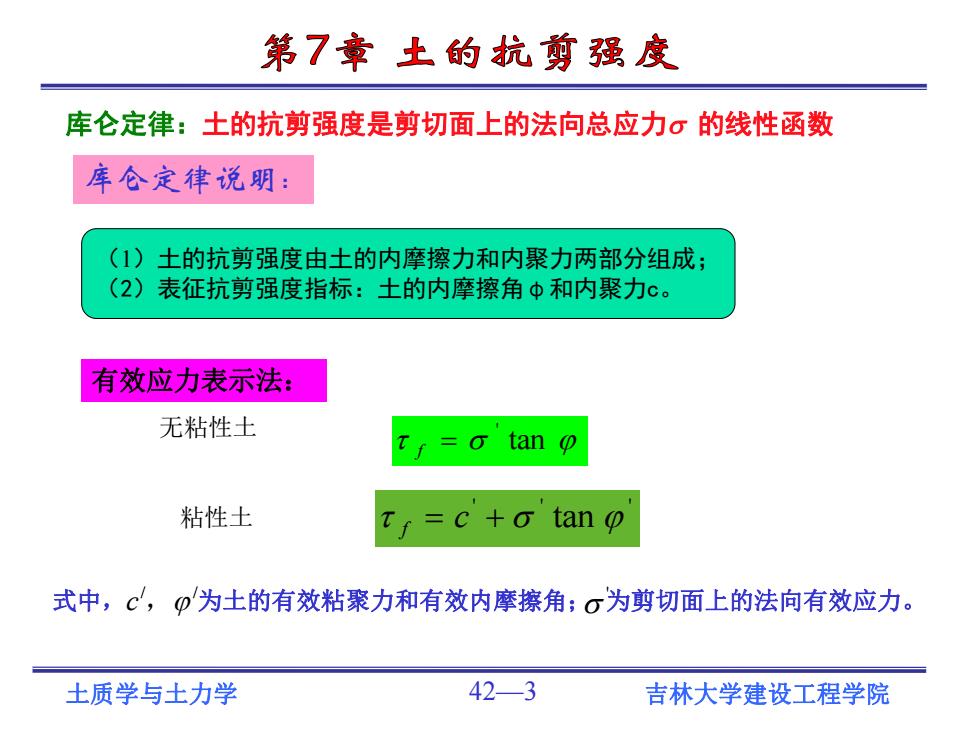
第7章土的抗剪强度 库仑定律:土的抗剪强度是剪切面上的法向总应力σ的线性函数 库仓定律说明: (1)土的抗剪强度由土的内摩擦力和内聚力两部分组成; (2)表征抗剪强度指标:土的内摩擦角中和内聚力c。 有效应力表示法: 无粘性土 T=o tan o 粘性土 =c +o tan o 式中,c,p为土的有效粘聚力和有效内摩擦角;σ为剪切面上的法向有效应力。 土质学与土力学 42-3 吉林大学建设工程学院
土质学与土力学 42—3 吉林大学建设工程学院 库仑定律:土的抗剪强度是剪切面上的法向总应力 的线性函数 (1)土的抗剪强度由土的内摩擦力和内聚力两部分组成; (2)表征抗剪强度指标:土的内摩擦角φ和内聚力c。 库仑定律说明: 有效应力表示法: tan ' f ' ' ' f c tan / / 式中,c , 为土的有效粘聚力和有效内摩擦角; 为剪切面上的法向有效应力。 无粘性土 粘性土 '

第7章土的抗剪强度 土体中某一点是否达到破坏的判定 TT 塑性破坏 试验表明,土的抗剪强度取决于土粒间的有效应力。 粘性士抗剪强度指标的选择 孔隙水压力能准确测定或计算出 地基或边坡的长期稳定性 有效应力 孔隙水压力难以测定或计算出 饱和粘土的短期稳定性 总应力 土质学与土力学 42-4 吉林大学建设工程学院
土质学与土力学 42—4 吉林大学建设工程学院 土体中某一点是否达到破坏的判定 试验表明,土的抗剪强度取决于土粒间的有效应力。 塑性破坏 极限平衡,临界状态 弹性平衡,安全 f f f 粘性土抗剪强度指标的选择 孔隙水压力能准确测定或计算出 地基或边坡的长期稳定性 有效应力 孔隙水压力难以测定或计算出 饱和粘土的短期稳定性 总应力
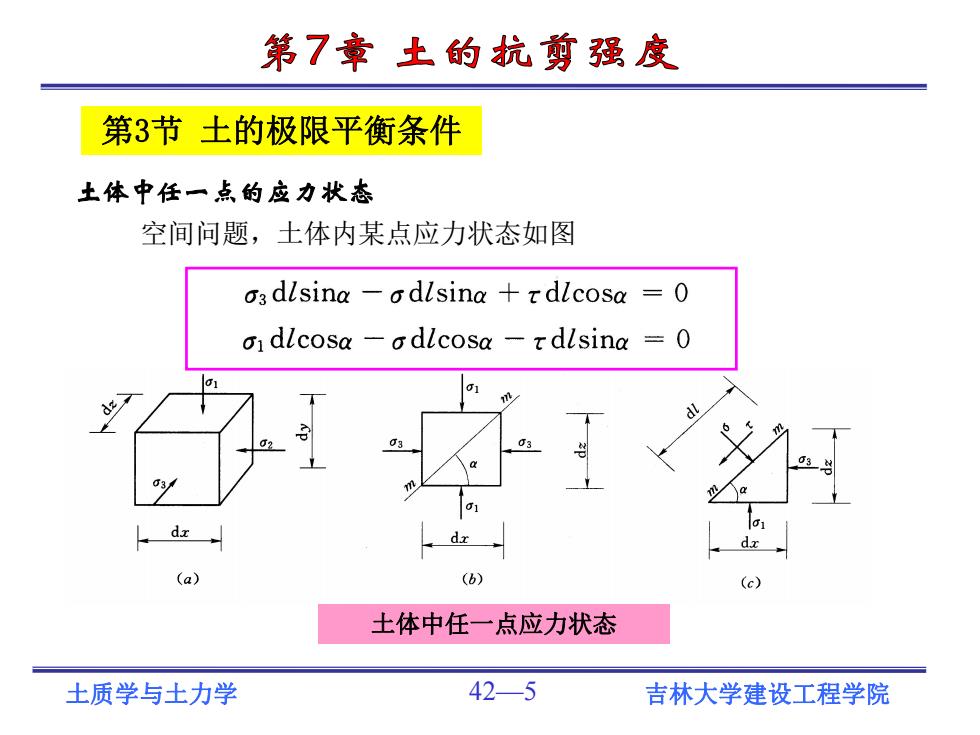
第7章土的抗剪强度 第3节土的极限平衡条件 土体中任一点的应力状态 空间问题,土体内某点应力状态如图 o3 dlsina-odlsina+r dlcosa =0 o dlcosa -odlcosa-tdlsina =0 a (b) (c) 土体中任一点应力状态 土质学与土力学 42-5 吉林大学建设工程学院
土质学与土力学 42—5 吉林大学建设工程学院 第3节 土的极限平衡条件 土体中任一点的应力状态 空间问题,土体内某点应力状态如图 土体中任一点应力状态

第7章土的抗剪强度 解上面方程可以得到m一m平面上的应力 2 cos2a 1-03 cos2 2a 2 2 2 g1-3 sin 2a →2 01-03 2 2 sin22a 上面两式相加 01+03 ×23 01-03 2 2 上式显然为一圆方程,圆心坐标为(何十0,0,半径为可, 这就是莫尔圆方程。 土质学与土力学 42-6 吉林大学建设工程学院
土质学与土力学 42—6 吉林大学建设工程学院 cos2 2 2 1 3 1 3 sin 2 2 1 3 cos 2 2 2 2 2 1 3 2 1 3 0) 2 ( 1 3 , 上式显然为一圆方程,圆心坐标为 , 半径为 2 1 3 解上面方程可以得到m—m平面上的应力 sin 2 2 2 2 2 1 3 上面两式相加 2 2 1 3 2 1 3 2 2 这就是莫尔圆方程
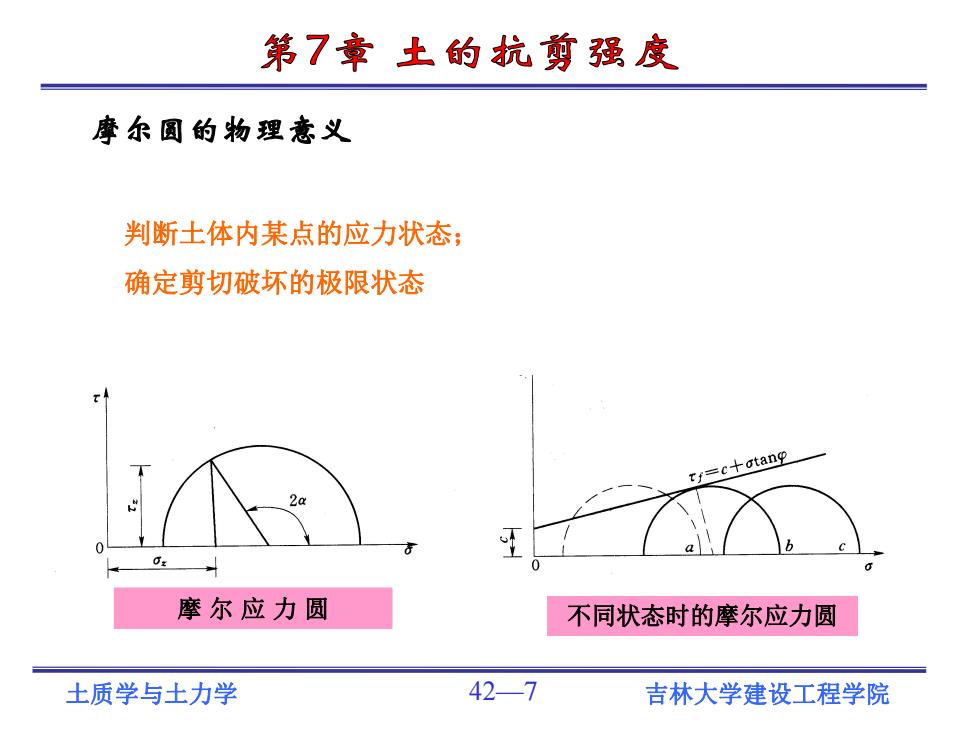
第7章土的抗剪强度 摩尔圆的物理意义 判断土体内某点的应力状态; 确定剪切破坏的极限状态 rf=c+atang 2a 0 摩尔应力圆 不同状态时的摩尔应力圆 土质学与土力学 42-7 吉林大学建设工程学院
土质学与土力学 42—7 吉林大学建设工程学院 摩 尔 应 力 圆 不同状态时的摩尔应力圆 摩尔圆的物理意义 判断土体内某点的应力状态; 确定剪切破坏的极限状态

第7章土的抗剪强度 土的极限平衡状态 土体达到极限平衡状态时,库仑强度线与摩尔圆相切。如 图,可得如下关系 AO1=BO1sing =(01-03)/2 BO =ccoto+(o1 +03)/2 (01 -03)/2 =[ccoto +(o1 +03)/2]sing 1 sing +2c coso 1 =03 1-sino 1-sing 利用三角函数关系,可得到处于极限平衡状态下某点主应力之间的关系 01 =o3tan2(45°+p/2)+2ctan(45°+p/2) 03 =o1tan2(45°-o/2)-2ctan(45°- p/2) 土质学与土力学 42—8 吉林大学建设工程学院
土质学与土力学 42—8 吉林大学建设工程学院 土的极限平衡状态 土体达到极限平衡状态时,库仑强度线与摩尔圆相切。如 图,可得如下关系 利用三角函数关系,可得到处于极限平衡状态下某点主应力之间的关系

第7章土的抗剪强度 对于无粘性土 a=o;tan2(45°+3) o;=o,tan2(45°-93) 根据三角形的几何关系,剪切破坏面与主应力面之间夹角 2=90°+p =45°+0 剪切破坏发生在与大主应力面成45°+中/2夹角的平 面上。因此可以判断土体中一点是否处于剪切破坏。 土质学与土力学 42-9 吉林大学建设工程学院
土质学与土力学 42—9 吉林大学建设工程学院 对于无粘性土 ) 2 tan (45 ) 2 tan (45 2 3 1 2 1 3 根据三角形的几何关系,剪切破坏面与主应力面之间夹角 2 90 45 剪切破坏发生在与大主应力面成45°+φ/2夹角的平 面上。因此可以判断土体中一点是否处于剪切破坏

第7章土的抗剪强度 【例题7-1】某土样p=26°,c=20kPa,承受o1=480kPa,3=150kPa的应力。试 根据极限平衡条件判断该土样所处的状态。 解:根据极限平衡条件,由已知求3计: o3计=itan2(45°-p/2)-2ctan(45°-p/2) =480×tan2(45°-26°/2)-2×20Xtan(45°-26°/2) =187.42-24.99 =162.43kPa o3=150kPa<o3计=162.43kPa 因此,该土样已破坏。 土质学与土力学 42-10 吉林大学建设工程学院
土质学与土力学 42—10 吉林大学建设工程学院