
(6 §2-5物体系的平衡·静定和超静定问题重点 9 P 厂静定问题:未知量数目等于独立平衡方程数目。 (超静定:未知量数目超过独立平衡方程的数目。 (静不定问题) 注:静不定次数(几次静不定):总未知量数目与总独立平衡方程数目之差。 (静不定问题需考虑变形条件补充方程。一变形体力学问题(举例:多人抬木头例子)) (简介静不定结构的优缺点:优点:提高承载能力:缺点:容易引起装配应力、温度应力问题等) 重点内容:物系的平衡问题! 例: A 己知:F ①M大小 求:图示位置平衡时 ②0处反力 ③AB杆受力 ④B处侧压力 (特点:“机构”平衡问题,平衡时主动力之间应保持一定关系) 解:(若先分析整体,则共有四个未知量。也可先由整体:∑F,=0→F) 可从已知主动力构件入手,例如:本题可先分析滑块B ①B (平面汇交力系问题,可求2个未知量) ∑F=0Fw-Fasin=0 「Fa ∑F,=0F-Fa cosp=0 ②轮 (平面任意力系问题,可求3个未知量) (或整体) ∑M。=0→M ∑F=0→F FA ∑F,=0→F 309F MAA M四 已知:M、q、E、1 C B 求:A、B两处约束反力 (注:绝不能将q合成为一个力作用在C处:) LLL山 基本部分(AC部分):靠自身可独立承受载荷的部分, 类型(一)结构特点:结构可分为 (附属部分(CD部分):靠自身不能独立承受载荷的部分, 方法:一般可先分析附属部分,再分析基本部分(或整体)
1 类型(一)结构特点:结构可分为 §2-5 物体系的平衡·静定和超静定问题 !!重点 静定问题:未知量数目等于独立平衡方程数目。 超静定:未知量数目超过独立平衡方程的数目。 (静不定问题) 注:静不定次数(几次静不定):总未知量数目与总独立平衡方程数目之差。 (静不定问题需考虑变形条件补充方程。 变形体力学问题(举例:多人抬木头例子)) (简介静不定结构的优缺点:优点:提高承载能力;缺点:容易引起装配应力、温度应力问题等) 重点内容:物系的平衡问题!! 已知:F ①M 大小 求:图示位置平衡时 ②O 处反力 ③AB 杆受力 ④B 处侧压力 (特点:“机构”平衡问题,平衡时主动力之间应保持一定关系) 解:(若先分析整体,则共有四个未知量。也可先由整体: Fy 0 Foy ) 可从已知主动力构件入手,例如:本题可先分析滑块 B (平面汇交力系问题,可求 2 个未知量) Fx 0 FN FB sin 0 FB Fy 0 F FB cos 0 FN (平面任意力系问题,可求 3 个未知量) Mo 0 M Fx 0 Fox Fy 0 Foy 已知:M、q、F、l 求:A、B 两处约束反力 (注:绝不能将 q 合成为一个力作用在 C 处!!) 基本部分(AC 部分):靠自身可独立承受载荷的部分, 附属部分(CD 部分):靠自身不能独立承受载荷的部分, 方法:一般可先分析附属部分,再分析基本部分(或整体) 30° 例: (6) 例: φ 例: ① φ ? ? ②轮 (或整体) ? ? ?

①CD 30 c ΣMe=0 Fa cos30'1-gl-7-Fc0s30°21=0→Fa P rΣF-0F-FBsm30°-Fsim30°=0→Fa C∑F,=0Fg-q1+Fg cos30°-Fc0s30°=0→Fg ②AC(或整体) ,∑F=0F-F4=0→F ?MA A (注意:F4=Fx而非F=-Fe×) ΣF,=0→F FAy? ΣM,=0M4-M-W当-21=0→M, (最后介绍第②步若不是分析AC,而是分析整体的解题思路) 例: /P 丝 求:A、B、C三处反力 解:分析:ABC为基本部分,CD为附属部分。 ①CD c ZMc=0 →F ∑F=0→Fa Fo? ΣF.=0 →F。(或∑MD=0) ②ABC(或整体) ΣM4=0→FB ∑MB=0→Fy(或ΣF,=O) ΣF=0 思考题: 思考 思考:求A、D两处反力的解题思路
2 C B FB F l l M o F l ql cos 30 2 0 2 cos 30 Fx Fc x FB F Fc x 0 sin 30 sin 30 0 y c y FB F o Fc y F 0 F q l cos 30 cos 30 Fx FAx Fcx FAx 0 0 (注意: Fcx Fcx 而非 Fcx Fcx ) Fy 0 FAy A A c y M A F l l M M M ql 2 0 2 3 0 (最后介绍第②步若不是分析 AC,而是分析整体的解题思路) 求:A、B、C 三处反力 解:分析:ABC 为基本部分,CD 为附属部分。 0 ( 0) 0 0 y Cy D x Cx C D F F 或 M F F M F x Ax B Ay y A B F F M F 或 F M F 0 0 ( 0) 0 思考:求 A、D 两处反力的解题思路。 ① 30° 30° ? ? ? ? ? ? ② (或整体) 例: α ? ? ? ① θ ② (或整体) M ? ? ? 思考题: 思考题: 思考题:
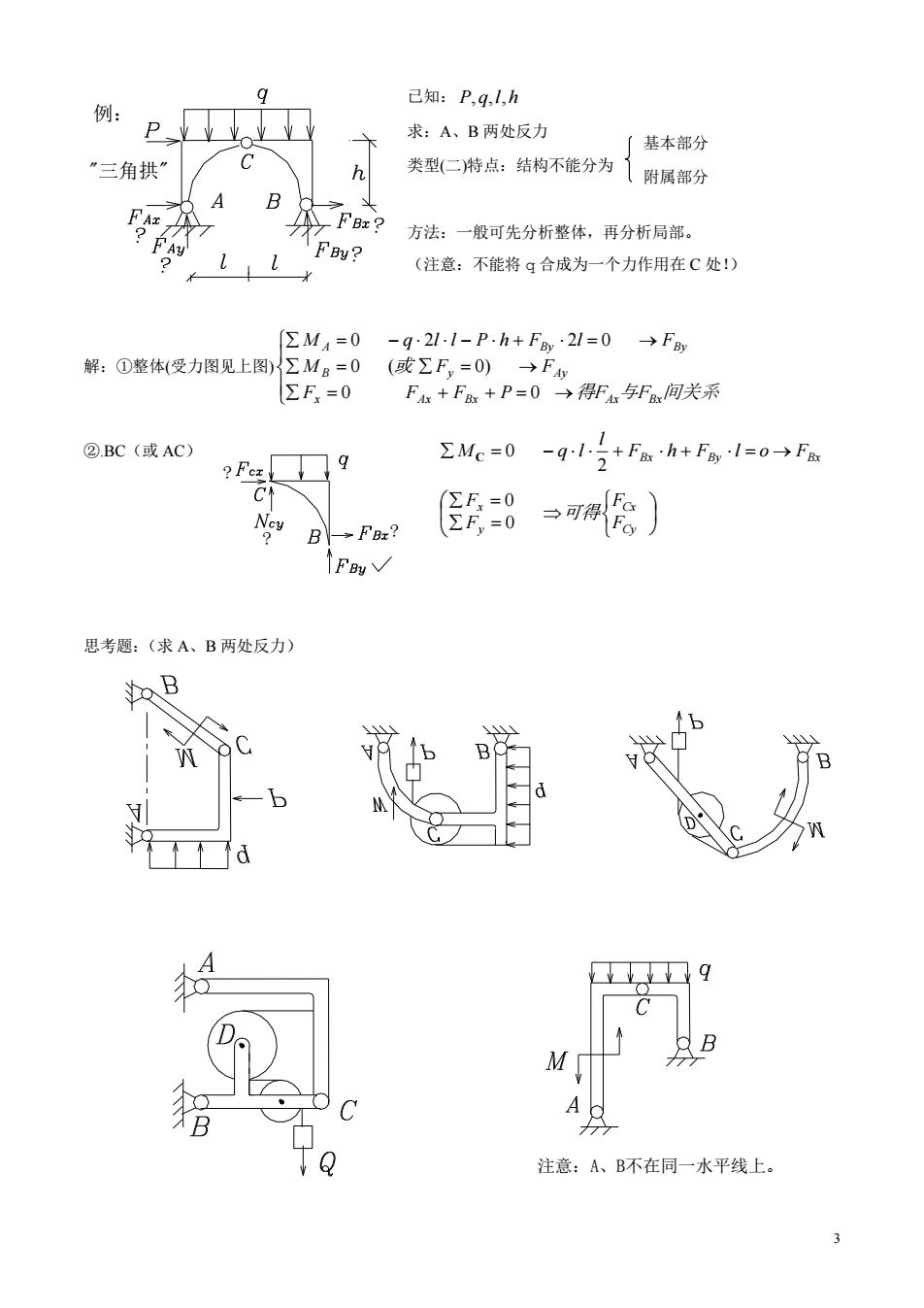
己知:P,ql,h 例: 求:A、B两处反力 「基本部分 ”三角拱” h 类到(二特点:结构不能分为1附属部分 A 方法:一般可先分析整体,再分析局部。 (注意:不能将q合成为一个力作用在C处:) [∑MA=0 -g21.1-P.h+F21=0 →F 解:①整体(受力图见上图)∑Mg=0(或∑F,=0)→F ΣF=0 Fx+F+P=0→得F与F间关系 ②.BC(或AC) ?Fc☐9 ∑Mc=0 -g1+Fah+F1=0→fa ΣF=0 B→FBx? ΣF,=0 →可得) FBNV 思考题:(求A、B两处反力) o B 5 A 9 M「 注意:A、B不在同一水平线上
3 已知: P, q,l, h 求:A、B 两处反力 类型(二)特点:结构不能分为 方法:一般可先分析整体,再分析局部。 (注意:不能将 q 合成为一个力作用在 C 处!) 解:①整体(受力图见上图) F F F P 得F 与F 间关系 M 或 F F M q l l P h F l F x Ax Bx Ax Bx B y Ay A By By 0 0 0 ( 0) 0 2 2 0 ②.BC(或 AC) Bx By o FBx F h F l l M q l 2 C 0 Cy Cx y x F F 可得 F F 0 0 思考题:(求 A、B 两处反力) 例: "三角拱" ? ? ? 注意:A、B不在同一水平线上。 基本部分 附属部分
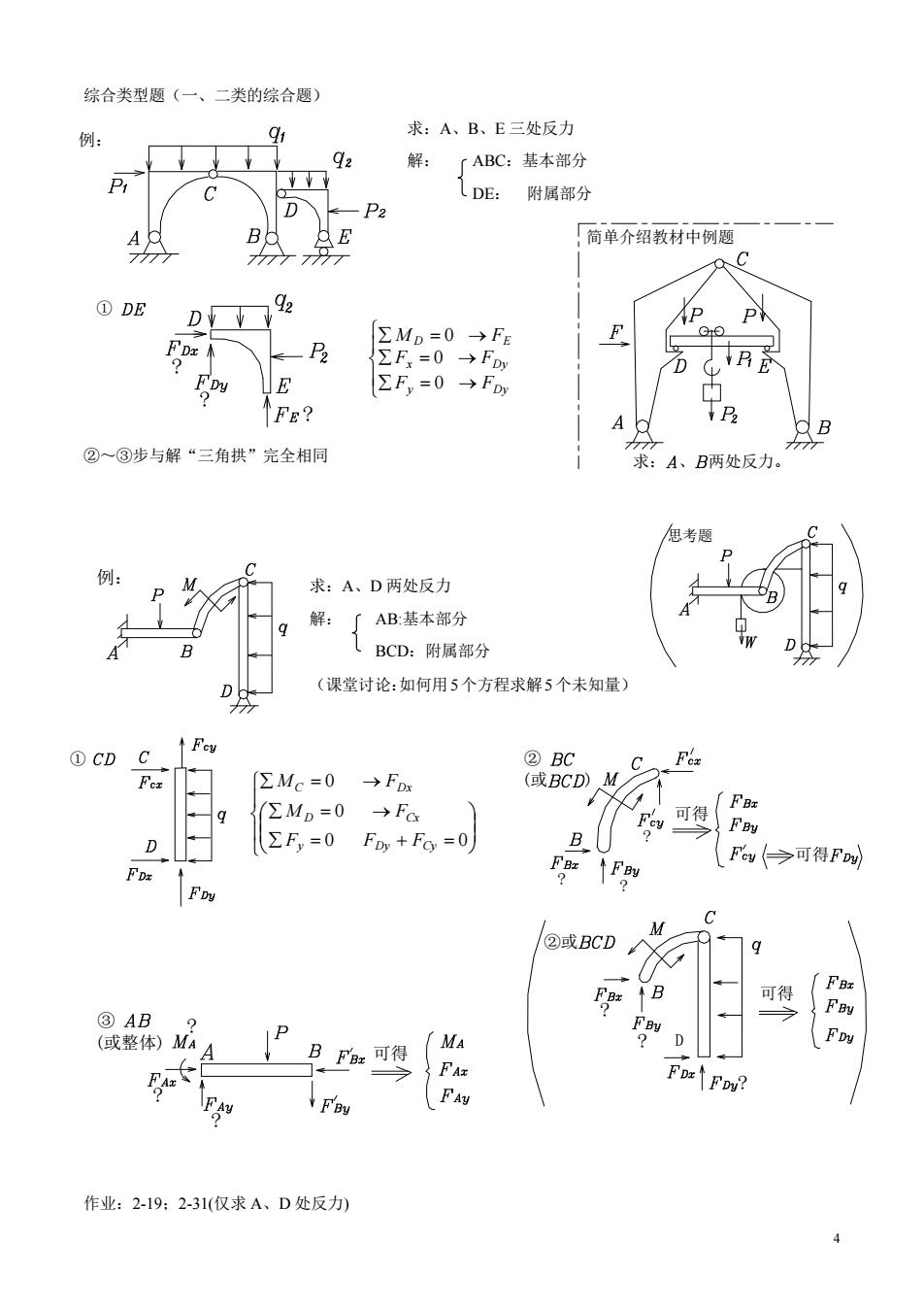
综合类型题(一、二类的综合题) 例: 求:A、B、E三处反力 解: 「ABC:基本部分 P DE:附属部分 D -P2 「简单介绍教材中例题 ①DE DV 92 ΣMD=0→FE ΣF=0→F E ΣF=0→F Fε? ②~③步与解“三角拱”完全相同 A B两处反力 求:A、D两处反力 解:了AB基本部分 1BCD:附属部分 D粉 (课堂讨论:如何用5个方程求解5个未知量) ①CDC ↑Few ②B F ∑Mc=0 →Fx q (EMD=0 →Fa Fa 可得F D ΣF,=0 FDy +Fo=0 B Fg→可得F ②或BCD M 可得 股24 ③AB PBF可 MA 、FA 作业:2-19:2-31(仅求A、D处反
4 综合类型题(一、二类的综合题) 求:A、B、E 三处反力 解: ABC:基本部分 DE: 附属部分 y Dy x Dy D E F F F F M F 0 0 0 ②~③步与解“三角拱”完全相同 求:A、D 两处反力 解: AB:基本部分 BCD:附属部分 (课堂讨论:如何用5个方程求解5个未知量) 0 0 0 0 y Dy Cy D Cx C Dx F F F M F M F 作业:2-19;2-31(仅求 A、D 处反力) 例: ? ? ? ① 简单介绍教材中例题 求: 、 两处反力。 例: ① ? ? ? D ? ? ? 可得 ② (或 ) ②或 可得 可得 ? ? ? 可得 ③ (或整体) 思考题