北京化工大学：《理论力学》课程教学资源（教案讲义）第四章 摩擦 §4-1 滑动摩擦 §4-2 摩擦角和自锁现象 §4-3 考虑摩擦时物体的平衡问题 §4-4 滚动摩阻的概念

(8) 第四章摩擦 (注：先安排学习第五章摩擦，再学第四章空间力系) 摩来是一种及夹复来的物理力学现象，涉及轻能面月部的弹性实形和清星论一 凸摩装机理的研究→摩学”学科 〔介绍工程中常用的近似理论 (本章限于“古典摩擦理论”范畴： 1讨论具有摩擦力作用的平衡问题 分类滑动摩标 ∫静摩擦 滚动摩阻 又1动摩 平7擎标 湿摩擦（举例：利、害两面，橡胶垫、下雨行车事） §4-1滑动摩擦 1.静滑动摩擦：（物体间有相对滑动趋势，但尚保持相对静止） 雨片m-0 P 静止平衡：有Fs=Q 保特静止令Q E:食动啤摧力：特点{②大小：在一定范围内变北 「①方向：与相对滑动趋势相反 即：0≤F3≤Fmax:且：Fma=f5·F ∫Fw:法向反力 、fg:静摩擦因（系）数 “静摩擦定律”（亦称“库仑摩擦定律” (E9:由实验测定。举例：摩托车赛车出发前，轮胎空转与地摩擦的作用) 2动滑动摩擦： (①方向：与相对滑动方向相反 F=FN(Fa=faFw)特点{②大小：无变化范围 (③-般：f<fs(fa<fs) (举例：推物滑动前后：斜板砂粒振落) (注：实际上fa与相对滑动速度有关，多数情况下，fa随速度增大而稍减小。 但当相对速度不大时，可以近似认为￡：为一常数) §4-2摩擦角和自锁现象 1、摩擦角的概念： 约束反力 F 一全约束反力：F4=F+F

1 则： 保持静止 第四章 摩擦 （注：先安排学习第五章摩擦，再学第四章空间力系） 接触面局部的弹塑性变形和润滑理论 表面物理和化学等问题 摩擦机理的研究  “摩擦学”（学科） 介绍工程中常用的近似理论 讨论具有摩擦力作用的平衡问题 滑动摩擦 静摩擦 干摩擦 滚动摩阻 动摩擦 湿摩擦 （举例：利、害两面，橡胶垫、下雨行车事） §4-1 滑动摩擦 1.静滑动摩擦：（物体间有相对滑动趋势，但尚保持相对静止） 静止平衡：有 FS  Q FS ：静(滑动)摩擦力。特点 即： 0  FS  Fmax ；且： S FN Fmax  f  “静摩擦定律”（亦称“库仑摩擦定律”） （fS：由实验测定。举例：摩托车赛车出发前，轮胎空转与地摩擦的作用） 2.动滑动摩擦： ①方向：与相对滑动方向相反 N F  fF ( d d FN F  f ) 特点 ②大小：无变化范围 ③一般：f ＜fS （fd ＜fS） (举例：推物滑动前后；斜板砂粒振落) （注：实际上 fd 与相对滑动速度有关，多数情况下，fd 随速度增大而稍减小。 但当相对速度不大时，可以近似认为 fd 为一常数） §4-2 摩擦角和自锁现象 1、摩擦角的概念： 约束反力  全约束反力： FRA  FN  FS 又 及 ①方向：与相对滑动趋势相反 ②大小：在一定范围内变化 （8） 摩擦是一种及其复杂的物理～力学现象。涉及 （本章限于“古典摩擦理论”范畴： 分类 FN：法向反力 fS：静摩擦因(系)数 φ FN FS

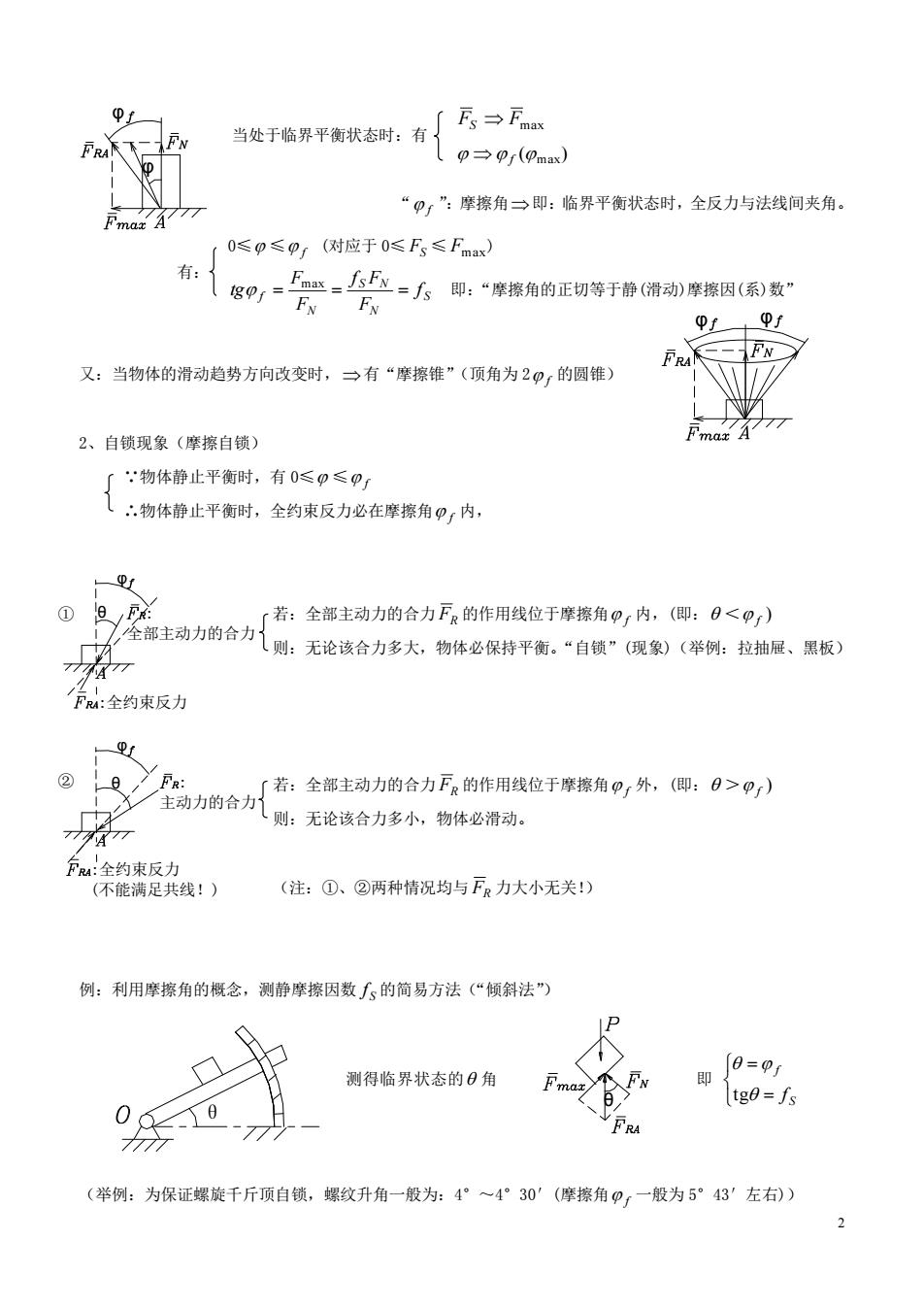
当处于临界平衡状态时：有厂厅→万 【p→pr(pmax) 77 “9,”:摩擦角→即：临界平衡状态时，全反力与法线间夹角。 0≤p≤pr(对应于0≤Fs≤Fmax) 有 巴=上=人5即：“摩擦角的正切等于静（滑动）摩擦因（系）数” N 又：当物体的滑动趋势方向改变时，→有“摩擦维”（顶角为2，的圆维） 2、自锁现象（摩擦自锁） ∫“物体静止平衡时，有0≤05， ∴物体静止平衡时，全约束反力必在摩擦角口，内， 若：全部主动力的合力FR的作用线位于摩擦角Q,内，（即：日P) 主动力的合力则：无论该合力多小，物体必滑动： 万。：全约束反力 (不能满足共线！) (注：①、②两种情况均与FR力大小无关) 例：利用摩擦角的概念，测静摩擦因数人、的简易方法(“领斜法”) 测得临界状态的日角 =p 06d 、10 举例：为保证螺旋千斤顶自锁，螺纹升角一般为：4°~4°30'（摩擦角,一般为5°43'左右）)

2 当处于临界平衡状态时：有 “ f ”：摩擦角  即：临界平衡状态时，全反力与法线间夹角。 有： 又：当物体的滑动趋势方向改变时，  有“摩擦锥”（顶角为 2  f 的圆锥） 2、自锁现象（摩擦自锁） ∵物体静止平衡时，有 0≤  ≤  f ∴物体静止平衡时，全约束反力必在摩擦角  f 内， 若：全部主动力的合力 FR 的作用线位于摩擦角  f 内，(即：  ＜ )  f 则：无论该合力多大，物体必保持平衡。“自锁”(现象)（举例：拉抽屉、黑板） 若：全部主动力的合力 FR 的作用线位于摩擦角  f 外，(即：  ＞ )  f 则：无论该合力多小，物体必滑动。 （注：①、②两种情况均与 FR 力大小无关！） 例：利用摩擦角的概念，测静摩擦因数 S f 的简易方法（“倾斜法”） 测得临界状态的  角 即      S f  f   tg （举例：为保证螺旋千斤顶自锁，螺纹升角一般为：4°～4°30′(摩擦角  f 一般为 5°43′左右)） φ φ FS  Fmax   ( max)  f 0≤  ≤  f (对应于 0≤ FS ≤ Fmax ) S N S N N f f F f F F F tg    max  即：“摩擦角的正切等于静(滑动)摩擦因(系)数” φ φ φ θ :全约束反力 ① : 全部主动力的合力 : 主动力的合力 φ ② θ :全约束反力 (不能满足共线！) θ θ

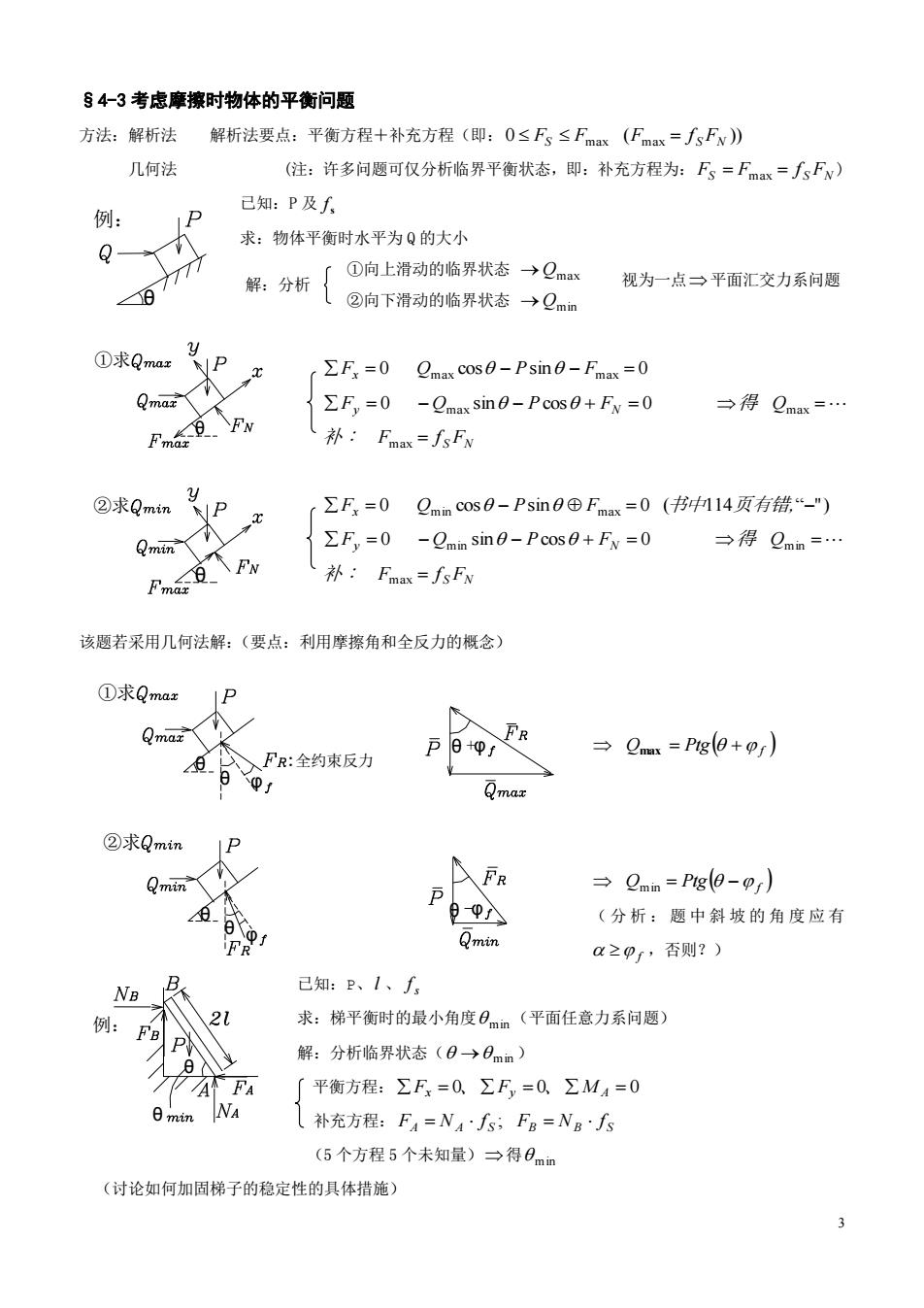
§4-3考虑摩擦时物体的平衡问题 方法：解析法解析法要点：平衡方程+补充方程（即：0≤F3≤Fma(Fmx=fsFw》 几何法 (注：许多问题可仅分析临界平衡状态，即：补充方程为：F=Fmx=∫Fv)》 例： 己知：P及人 Q 求：物体平衡时水平为Q的大小 8力7 解：分析 「①向上滑动的临界状态→0a 视为一点→平面汇交力系问题 (②向下滑动的临界状态→Qmm ①求Qma F=0 Omax cos0-Psine-Fmax =0 EF =0-Qmax sin0-Pcos0+FN=0 →得Qma=… 补：Fmax=fsFN ②求Qmin ,∑F=0 min cos0-Psin0©Fmax=0(书14页有错“-") EFy=0 -Qmnin sin0-Pcos0+Fy =0 →得Qmn=· Pn&w 补：Fmax=fsFN 该题若采用几何法解：（要点：利用摩擦角和全反力的概念） ①求Qmax IP FR 三Qm=-Pg9+pr） FR:全约束反力 ②求Qmin P 入FR →Qmn=Pg0-pr） 日9入 (分析：题中斜坡的角度应有 a≥pj,否则？) 己知：P、1、f Fa 求：梯平衡时的最小角度日m血（平面任意力系问题） 解：分析临界状态(0→日mm） 「平衡方程：∑F=0.∑F,=0∑M4=0 日mn 补充方程：FA=NAfs;FB=NB·fs (5个方程5个未知量)→得0mm (讨论如何加固梯子的稳定性的具体措施)

3 解：分析 θ :全约束反力 ①求 θ φ θ +φ §4-3 考虑摩擦时物体的平衡问题 方法：解析法 解析法要点：平衡方程＋补充方程（即： 0 max ( max )) S S FN  F  F F  f 几何法 (注：许多问题可仅分析临界平衡状态，即：补充方程为： S S FN F  Fmax  f ) 已知：P 及 s f 求：物体平衡时水平为 Q 的大小 ①向上滑动的临界状态 Qmax ②向下滑动的临界状态 Qmin  Fx  0 Qmax cos  Psin  Fmax  0  Fy  0  Qmax sin  Pcos  FN  0 得 Qmax  S FN 补： Fmax  f  F  0 Qmin cos  Psin  Fmax  0 (书中114页有错， “") x    Fy  0  Qmin sin  Pcos  FN  0 得 Qmin  S FN 补： Fmax  f 该题若采用几何法解：（要点：利用摩擦角和全反力的概念）    Qmax  Ptg   f    Qmin  Ptg   f （ 分 析 ： 题 中 斜 坡 的 角 度 应 有   f ，否则？） 已知：P、l 、 s f 求：梯平衡时的最小角度  min （平面任意力系问题） 解：分析临界状态（   min ） 平衡方程：  Fx  0、  Fy  0、  M A  0 补充方程： A A S B B S F  N  f ; F  N  f （5 个方程 5 个未知量）  得  min （讨论如何加固梯子的稳定性的具体措施） 视为一点  平面汇交力系问题 例： θ ①求 θ θ 例： θ θ ②求 θ ②求 θ φ θ -φ

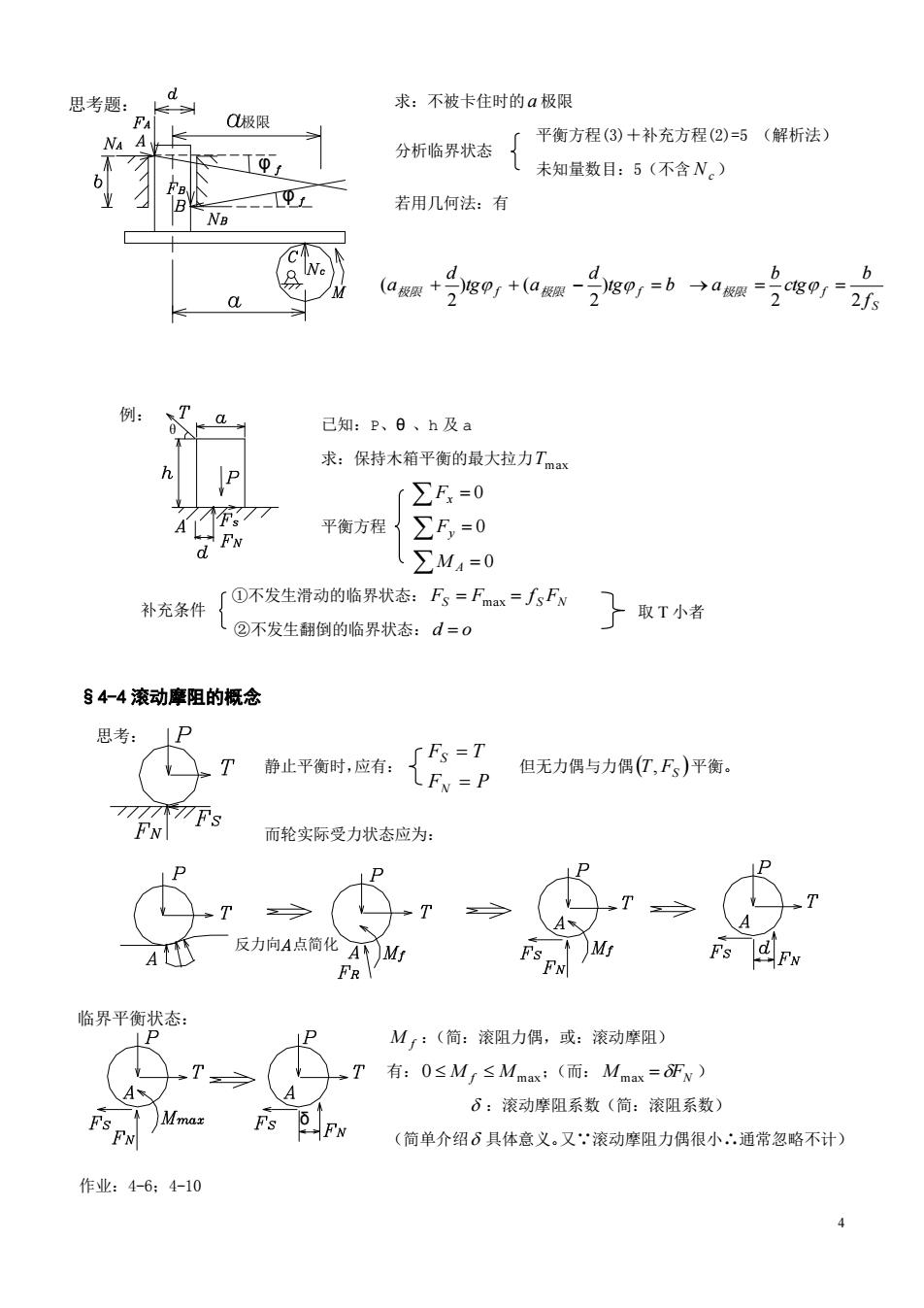
思考题： 色人 求：不被卡住时的a极限 Q极限 NA 平衡方程(3)+补充方程(2)=5（解析法） Io, 分析临界状态 未知量数目：5（不含N) 若用几何法：有 NB e 例： T 已知：P、0、h及a h 求：保持木箱平衡的最大拉力Tmx ∑F=0 平衡方程{∑F,=0 ∑MA=0 补充条件 「①不发生滑动的临界状态：Fs=Fmax=fsFN 【②不发生翻倒的临界状态：d=0 了取T小者 §4-4滚动摩阻的概念 思考：P T 时低 但无力偶与力偶（亿，F)平衡。 而轮实际受力状态应为： P 一反力向A点简化 M Fs dFN 临界平衡状态： Mr:(简：滚阻力偶，或：滚动摩阻) T 有：0≤M≤Mmx:(而：Mmax=F) Fs FN 6:滚动摩阻系数（简：滚阻系数} Fs FN (简单介绍6具体意义。又：滚动摩阻力偶很小∴通常忽略不计) 作业：4-6；4-10

4 分析临界状态 F P F T N S   求：不被卡住时的 a 极限 平衡方程(3)＋补充方程(2)=5 （解析法） 未知量数目：5（不含 Nc ） 若用几何法：有 S 极限 f 极限 f 极限 f f b ctg b tg b a d tg a d a 2 2 ) 2 ) ( 2 (           已知：P、θ 、h 及 a 求：保持木箱平衡的最大拉力 Tmax Fx  0 平衡方程 Fy  0 M A  0 ①不发生滑动的临界状态： S S FN F  Fmax  f ②不发生翻倒的临界状态： d  o §4-4 滚动摩阻的概念 静止平衡时，应有： 但无力偶与力偶   T FS , 平衡。 而轮实际受力状态应为： M f ：（简：滚阻力偶，或：滚动摩阻） 有： 0  M f  Mmax ；（而： Mmax  FN ）  ：滚动摩阻系数（简：滚阻系数） （简单介绍  具体意义。又∵滚动摩阻力偶很小∴通常忽略不计） 作业：4-6；4-10 极限 φ φ 思考题： 取 T 小者 例： θ 思考： 反力向 点简化 补充条件 临界平衡状态： δ