同济大学：《结构动力学》课程教学资源（教案讲义）Lecture 02.pdf_大学文库

2014/5/12 2 Structural Dynamics: Lecture 2 7  Absolute vs. Relative responses x t 3   x t 2   x t 1   M X C X K X M I           g     x   1 2 3  , ,     T X    x t x t x t   Can we compare them? Free vibration of SDOF  A structure is said to be undergoing free vibration when it is disturbed from its static equilibrium position and then allowed to vibrate without any external dynamic excitation.  Undamped /damped free vibration Structural Dynamics: Lecture 2 8 Free vibration of SDOF Structural Dynamics: Lecture 2 9 • Equation of motion of SDOF system mu cu ku f t        0 0 0 f t freevibration c undamped free vibration c damped free vibration             Structural Dynamics: Lecture 2 10 Undamped Free Vibration  Problem statement differential equation governing the vibration of the system the system will be disturbed by mu ku   0     0 0 initial displacement initial velocity u u u u   ( ) 2 2 f x dt d x  Structural Dynamics: Lecture 2 11  REVIEW: Solution theory for non-homogeneous linear differential equations of second order y py qy f t      y t    y t c   y t p   yc (t) : Complementary solution, i.e. the complete solution to the homogeneous differential equation. (f(t) =0) transient vibration / eigenvibration yp (t) : Particular solution (due to f(t) steady-state vibration / stationary vibration 12  Solution of Free vibration of Undamped SDOF– Method I  The general solution will have the form 1 2 u t A t A t ( ) cos sin     mu ku   0     0 0 initial displacement initial velocity u u u u     0 u t t ( ) cos sin 0 u u  t    u t t ( ) cos   A            2 2 0 0 0 arctan 0 u u A u u                    

2014/5/12 3 Structural Dynamics: Lecture 2 13  Solution of Free vibration of Undamped SDOF –Method II  From mathematical theory, the solution to the above linear, homogeneous, second-order differential equation with constant coefficients has the following form A: constant s:unknown coefficient  Bring the solution to the equation of motion leading to the characteristic equation  One has two imaginary roots ( ) st u t Ae  mu ku   0   2 0 st ms k Ae   2 2 / n s k m     1 2 1 n n n k s s w i i i here m          Structural Dynamics: Lecture 2 14  The general (complementary) solution of the EOM will be A1, A2 are complex constants  Introduce Euler’s pair (Euler relations), which are  Notice the vibration must be real, A, B are real-valued constants   0 0 cos sin cos sin n n n n n u u t A t B t u t t                  1 2 1 2 1 2 n n s t s t i t i t u t Ae A e Ae A e       cos sin cos sin ix ix e x i x e x i x      Structural Dynamics: Lecture 2 15  The velocity and acceleration will be  Substitute the initial condition  The final solution is       2 2 cos sin sin sin cos cos n n n n n n n n n n u t A t B t u t A t B t u t A t B t                       0 0 0 0 t t n u u A u u B          0 0 cos sin cos sin n n n n n u u t A t B t u t t                Structural Dynamics: Lecture 2 16  Important dynamic properties n k m   Natural circular frequency of vibration 2 n n T    Natural period of vibration 2 n n f    Natural cyclic frequency of vibration Structural Dynamics: Lecture 2 17 F1=0.45Hz (T1=2.22s, H=100m) F1=0.16Hz (T1=6.25s, H=495m) F1=0.1475Hz, (T1=6.77s), L=1088m F1=0.1475Hz, (T1=6.77s), L=1377m Structural Dynamics: Lecture 2 18  Free vibration curve of undamped SDOF due to initial displacement and velocity

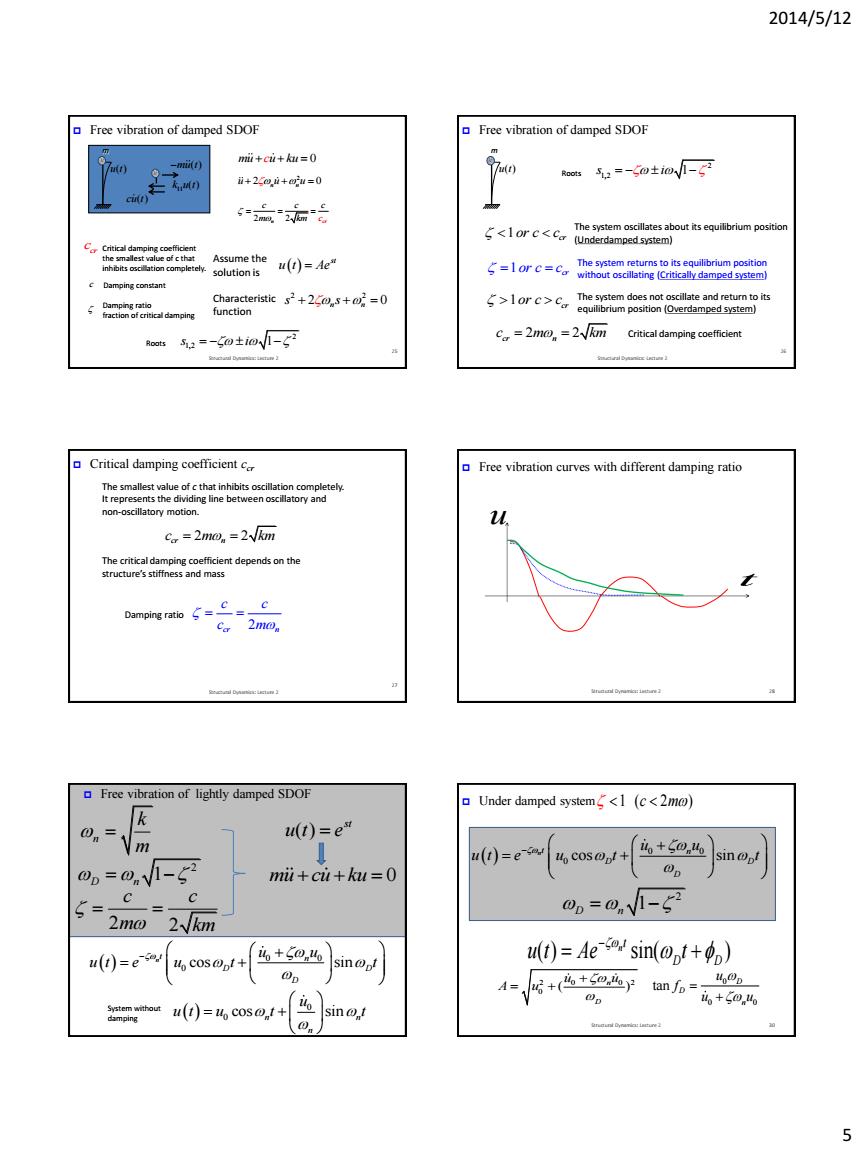
2014/5/12 5 Structural Dynamics: Lecture 2 25 m ut() mu t() 11 k u t() cu t()  Free vibration of damped SDOF cr c Critical damping coefficient the smallest value of c that inhibits oscillation completely. Damping constant Damping ratio fraction of critical damping Assume the solution is Characteristic function mu u k    c u 0 2 2 0 n n u u u      2 n 2 cr c c c m km c        st u t Ae  2 2 2 0 n n s s      2 1,2 Roots s i        1  c Structural Dynamics: Lecture 2 26 m ut()  Free vibration of damped SDOF 1 cr    or c c The system oscillates about its equilibrium position (Underdamped system) The system returns to its equilibrium position without oscillating (Critically damped system) The system does not oscillate and return to its equilibrium position (Overdamped system) 2 2 cr n c m km    Critical damping coefficient 1 cr    or c c 1 cr    or c c 2 1,2 Roots s i         1 Structural Dynamics: Lecture 2 27  Critical damping coefficient ccr The smallest value of c that inhibits oscillation completely. It represents the dividing line between oscillatory and non-oscillatory motion. The critical damping coefficient depends on the structure’s stiffness and mass Damping ratio 2 cr n c c c m     2 2 cr n c m km    Structural Dynamics: Lecture 2 28 t u  Free vibration curves with different damping ratio  Free vibration of lightly damped SDOF mu cu ku    0 ( ) st u t e  n k m   2 2 c c m km       0 0 0 cos sin n t n D D D u u u t e u t t                          0 0 cos sin n n n u u t u t t            2 1    D n   System without damping Structural Dynamics: Lecture 2 30  Under damped system    1 ( 2 ) c m   0 0 0 cos sin n t n D D D u u u t e u t t                        2 1    D n   ( ) sin( ) n t D D u t Ae t       2 2 0 0 0 ( ) n D u u A u      0 0 0 tan D D n u f u u    