
Chapter 10. Method of Consistent Deformations(协调变形法) (and Other Compatibility Methods). 月济大学 土工程学院 TONGJI UNIVERSITY 10.3 determination of redundant reactions( ) Ma=R4 Rax=R3 1=0 Ray=R2 Rby=Ri (a) R40 A10 +/11R1=A1 R30 410 R10=0 AIR=RI R20 R1=(A1-A10) (b) /u Rg=Ro + RaR R41 R31 hi S=S0+ SIR R11=1 2 R21
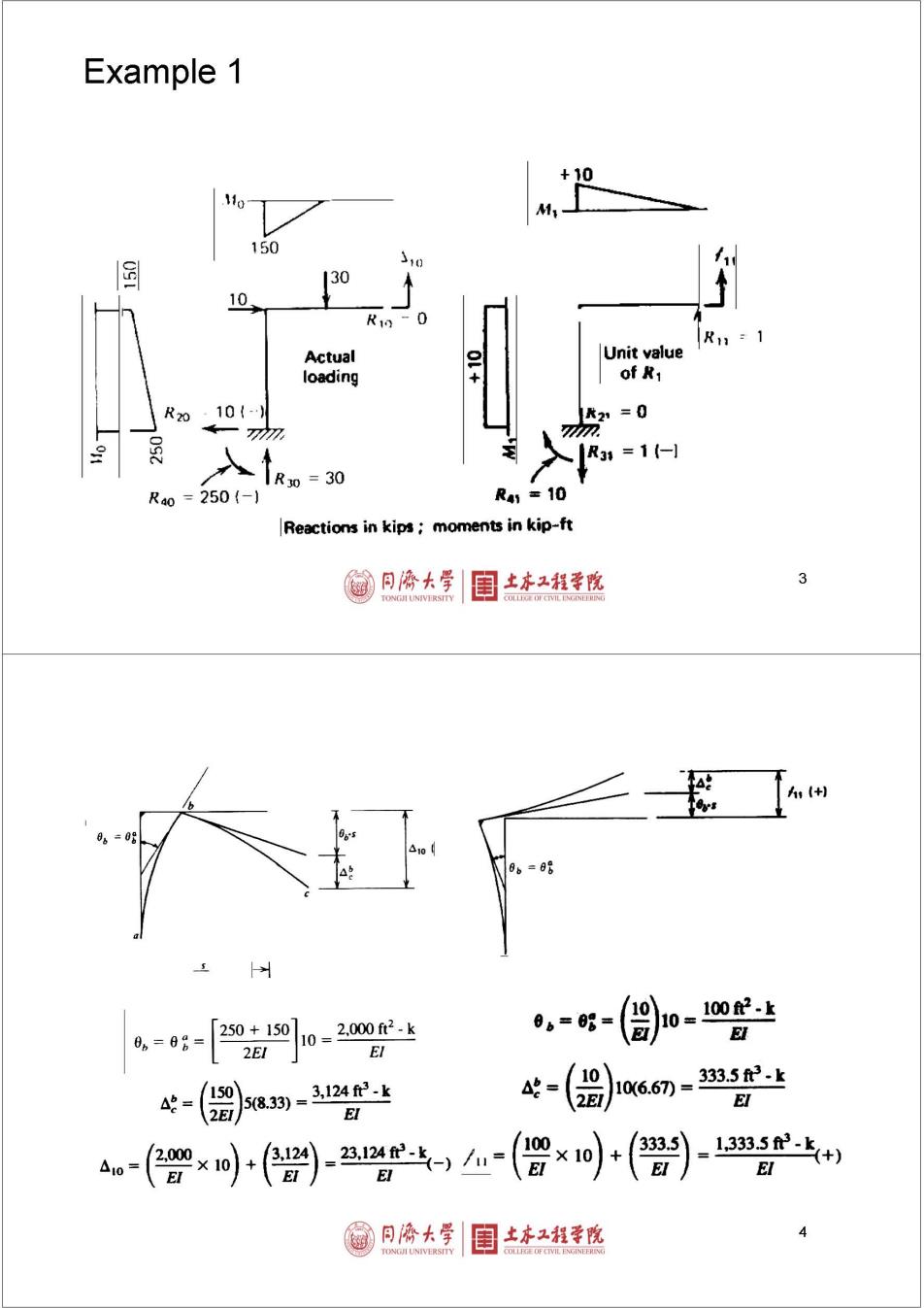
Example 1 +10 150 国 )10 30 10 R- 0 R:1 Actual Unit value loading of R1 R20·10(- 21=0 m 入R3=1- 1R0=30 R40=250(-J R41=10 Reactions in kips;moments in kip-ft 同©大学 土亦工程学院 06=88 06=08= 100.上 0。=08= 2,000f2.k El 4-(留324 A= 10 106.67= 33.53.k 4w-(智×+()-a2当-(智×0)+() 133350上+) El 同桥大学 土床工程学晚
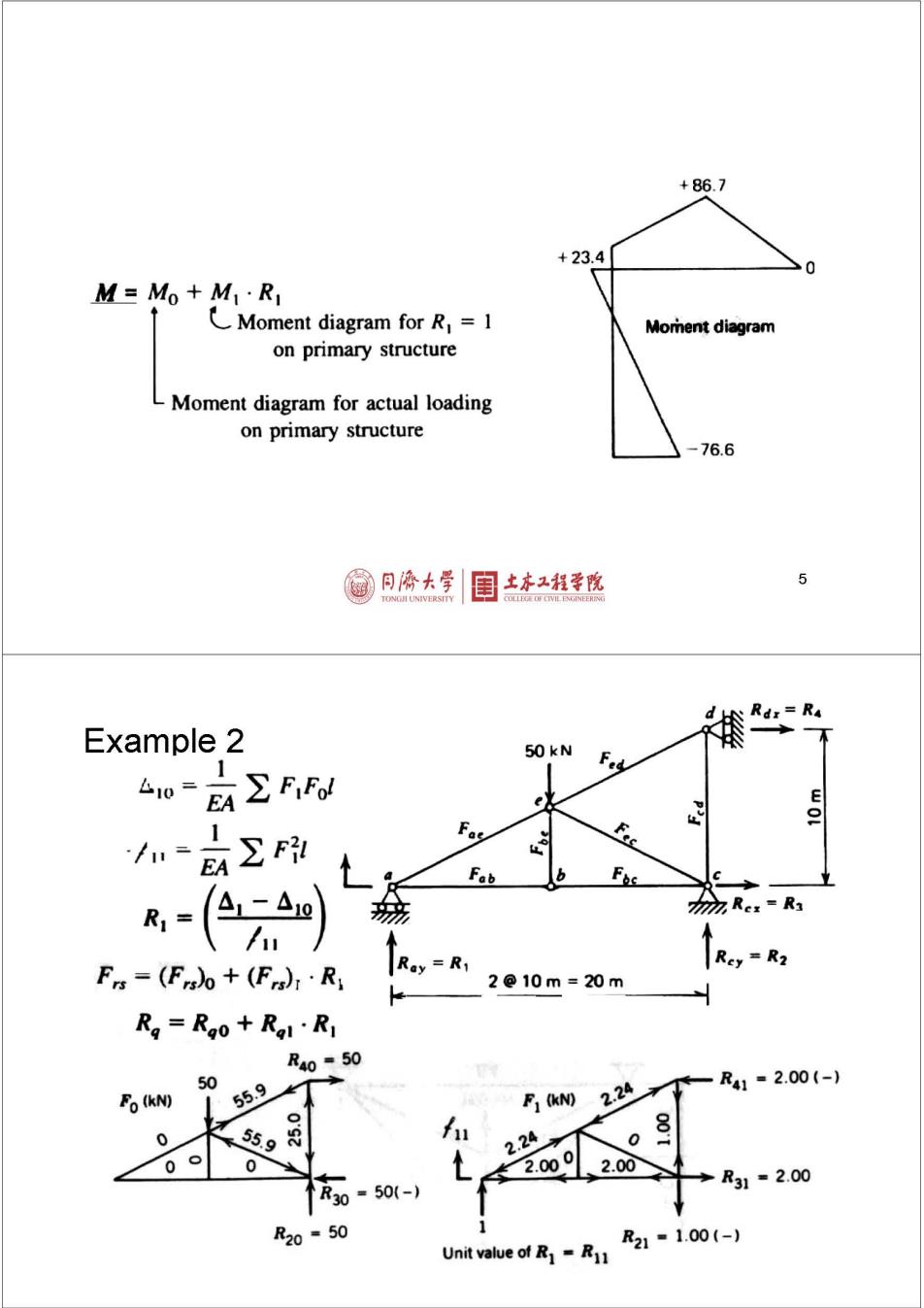
+86.7 +23.4 M=Mo+M1·R1 CMoment diagram for R=1 Moment diagram on primary structure Moment diagram for actual loading on primary structure -76.6 月大学 土亦工程学院 5 d Rd:=R4 Example 2 50kN 10 EA∑R Fab Rcx=R3 Rey=R2 Fs=(Fo+(F)·R, Ray =R1 2@10m=20m Rg=Rg0+Rg1·R1 R40=50 50 R41=2.00(-) Fo (kN) 55.9 月1kN2.24 8 0 2.24 0⊙ 0 2.000 2.00 R30=50(-) R31=2.00 R20=50 R21=1.00(-) Unit value of R=R1

10.5 support settlements(支座沉降) and elastic supports Chord connecting supports of primary structure 2 /11R1+/12R2=△1-△10 /2R1+/22R2=42-420 么-剑 +△20 同源大学 目±本赢nward settlements R1=k(-△) =- R,=V+1k) 同停大学 目 土亦工程学院

10.10 determination of redundant member forces for truss structures 了,bar forces (Fabl R1产 R21 (c) R31 △10+△1R=0 △1R=/1X S=So+SX1 同 9 Example 110= ΣR风 ∑ 53.3 。=0 Fo (kN) 75.4 378 3m.8 6.7 26.7 20.7 1R=80 R0=53.3 R0=287 707 a小1=X=1 (kN) 707 0 R1=0 R21=0 R31=0
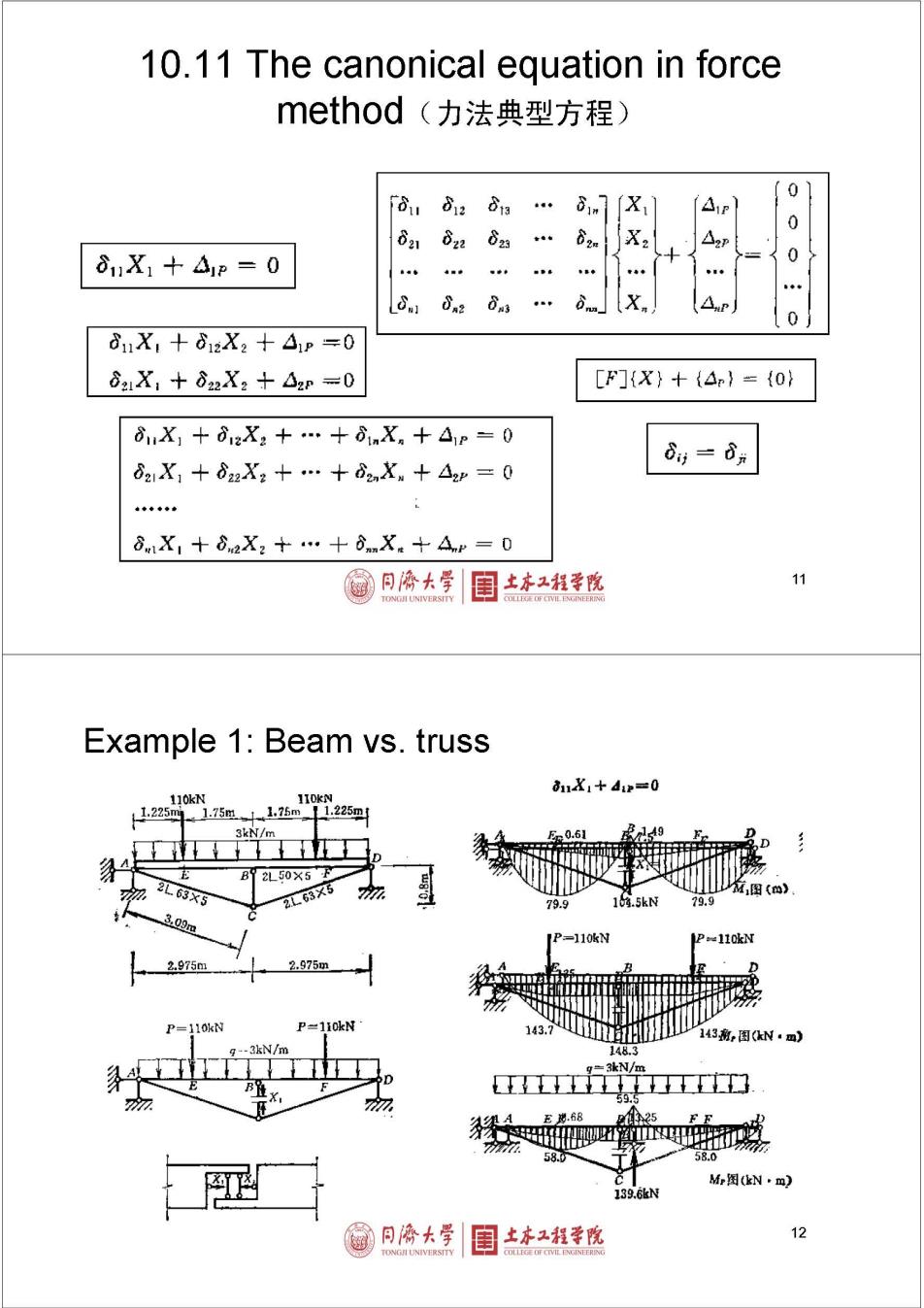
10.11 The canonical equation in force method(力法典型方程) TSu 0 812 83 81m Air X. 0 621 822 62e △ 81X1十△1p=0 0 8 2 6n3 81X,+812X2十41P=0 821X,+822X2+△2r=0 [F]{X}+{4}={0} 8,X1+d1zX2+…+8nXn+△1r=0 6=6n 821X1+822X2+…十d2nXm+△2r=0 4中+◆ 81X,+62X2+…十6nX。+Ar 0 同©大学 土本工程学院 11 TONGI UNIVERSITY Example 1:Beam vs.truss 1X1+d=0 110kN 11225 1.75m+175m 1.225m 3kN/m E0.61 8149 2L50X5 2L.63X5 2L63X5 M图(m》 79.9 10.5kN 79,9 3.09m 1P=110kN P110kN 2.975m 2.975m P=110kN P=110kN 143.7 143,图N,m) g--3kN/m 148.3 g=3kN/m LL口 E.68 325FF 58.0 58.0 Mr图(N·m) 139.6kN 同©大学 土本工程学院 12

Example 2:Remove or cut? inX,+8nX2+…+dxn+ 5h*¥¥十 =0 n ×D= 3E7 6 6 11 2 δm E75×2I×2× ×2)= 81 3EI EA +*,262 48E7 PI 11P3 8E713 Example3:Elongation(伸长)plus bending -50 -50 +250 +25 61X1+d1=0 480 213 8t=3E 4,-》a@7+2ew -24525X-1-25+0x×1x1 =-320al 同©大学 土亦工程学院 14
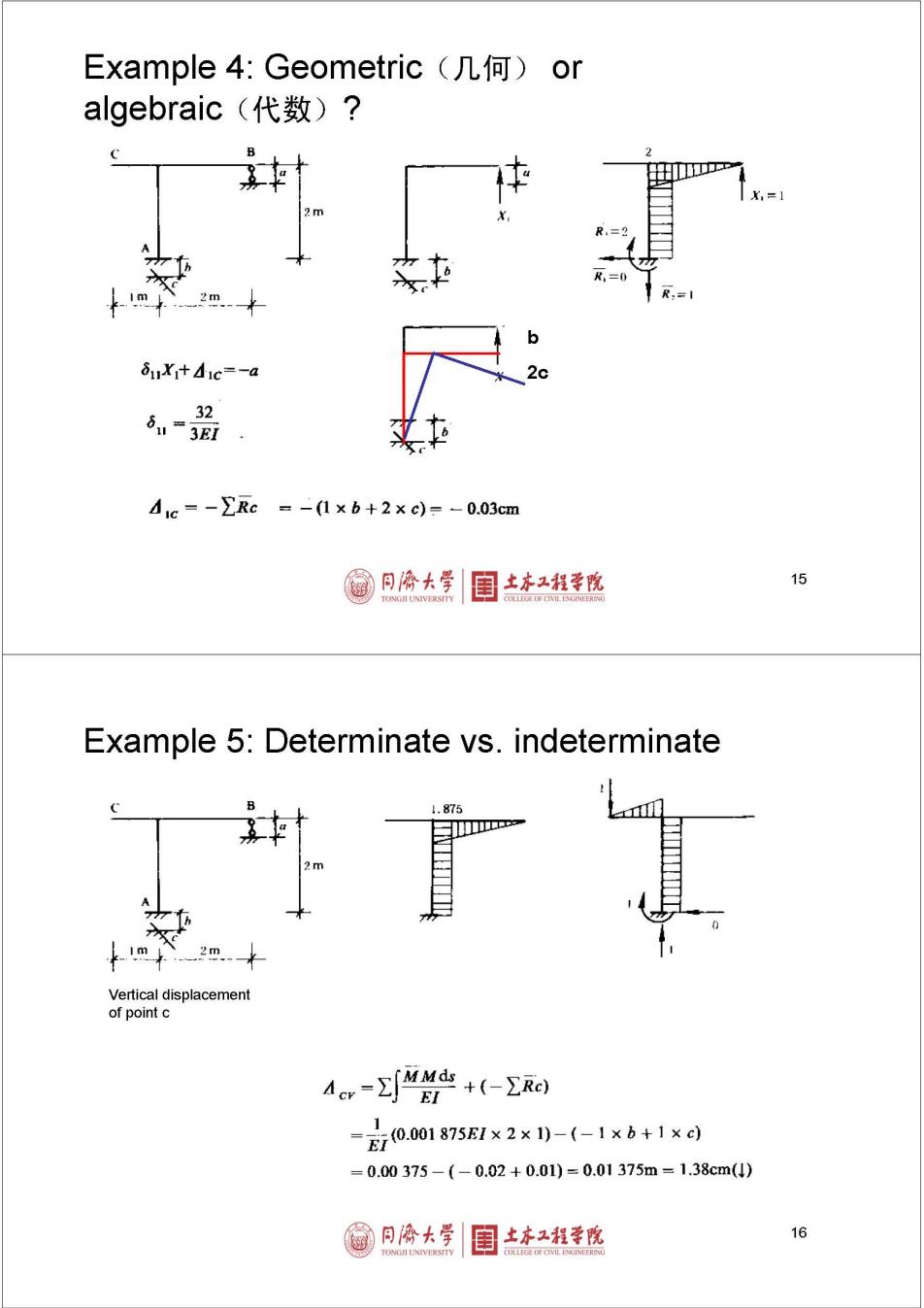
Example4:Geometric(几何)or algebraic(代数)? X,=1 2 m 1 R,=1 8uX+4ic=-a 32 6,=3Ei 4c=-∑Rc=-1×b+2×c)=-0.03cm 同海大学 土本工程学院 15 Example 5:Determinate vs.indeterminate 1.875 2m 2m. Vertical displacement of point c 4m-产+(-Σ网 =00187581×2×)-(-1×b+1×d =0.00375-(-0.02+0.01)=0.01375m=1.38cm(J) 同停大学 土亦工程学院 16
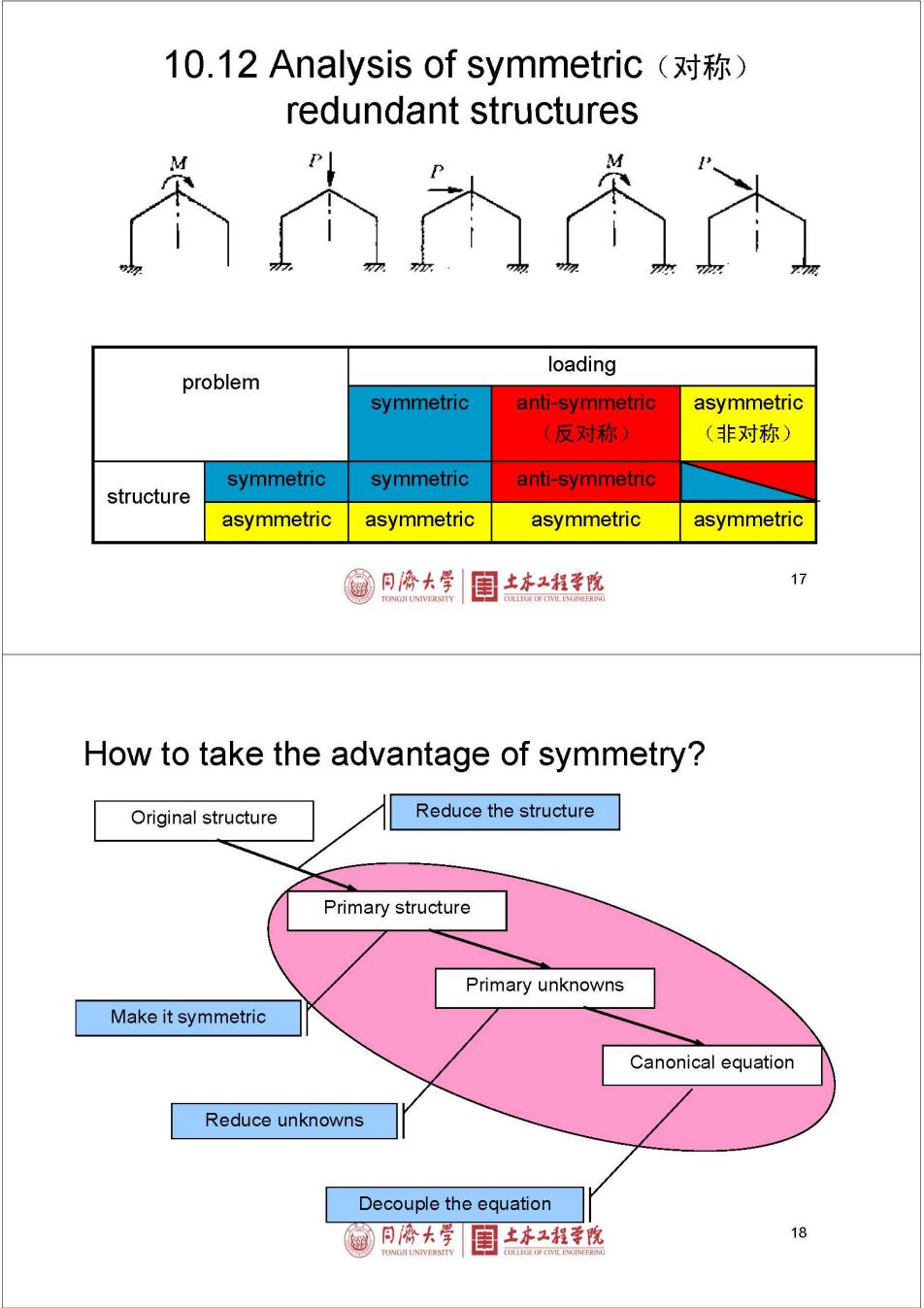
10.12 Analysis of symmetric(对称) redundant structures 个六 loading problem symmetric anti-symmetric asymmetric (反对称) (非对称) symmetric symmetric anti-symmetric structure asymmetric asymmetric asymmetric asymmetric 同海大学 土亦工程学院 17 How to take the advantage of symmetry? Original structure Reduce the structure Primary structure Primary unknowns Make it symmetric Canonical equation Reduce unknowns Decouple the equation 制凡陈大学 目 土亦工程学院 18

Example 1 611X1+612X2十81aXg+4r=0 621X1+622X2+63X3+42p=0 81X1+832X2+b3X3+Ap=0 0 d11X,+01eX:+d=0 02X:+02zX2+42p=0 d33X3十d3e=0 @海大学 土本工程学院 19 Reduce the structure to a half structure frames with odd spans 同桥大学 目 土亦工程学院 20