《断裂力学》课程教学资源（书籍教材）断裂力学教程电子版（PDF电子书，共四章）

第一章线弹性断裂力学基础 1.1引言 断裂力学是近半个世纪以来发展起来的一门新学科。它主要研究带裂纹固体的强度 和裂纹传播的规律。对于不同条件下的不同材料，人们往往根据自己的目的，将材料抽 象为某种“理想物质”以反映某些最重要的特性。在研究断裂问题时，将材料抽象为理 想线弹性体就是线弹性断裂力学。如果再考虑裂纹尖端塑性区就有弹塑性断裂力学。不 少情况下，温度的影响和“时间效应”都不能忽略。从流变学观点出发考虑到材料的流 变性能就有流变断裂学，它还可以细分为粘弹性断裂力学，粘弹塑性断裂力学，热粘弹 性断裂力学，热粘弹塑性断裂力学等。目前只有线弹性断裂力学发展比较成熟，并已制 定出规范（例如美国机械工程师协会ASEM,锅炉与压力容器规范等）。编成手册应用 于生产上。 断裂力学涉及内容很广，这里只介绍一些基础性的内容。中国有句古话：“吃一堑， 长一智”。吃一次亏，出来一门新学科。断裂力学可以说是人类吃了大亏，从总结惨痛 血的教训中产生的。生产推动了科学发展，科学反过来又促进生产以更高的速度向前发 展。在这个过程中，旧的问题不断解决，新的矛盾又不断产生。最初，人们为了提高材 料的强度防止脆断，制成了钢材等塑性材料。进一步提高塑性材料的强度是通过阻止屈 服（阻止位错运动）来实现的。再进一步提高强度就出现了新的矛盾，强度高了，韧度 却低了，构件常在应力不高，甚至低于屈服极限的情况下发生突然的脆性破坏。如焊接 铁桥的突然倒塌，焊接轮船的脆性破坏，各种球罐的突然爆炸等等，均不能用传统的建 立在连续性假设基础上的强度科学（如材料力学）来解释。随着生产的发展，大量采用 新材料（高强度钢、复合材料、塑料）新工艺，新的工作条件（高温、高速、高压、低 温)等，致使古典强度科学无法适应新的生产水平的需要。对低应力脆断事故进行大量 分析研究表明脆性断裂是由于宏观缺陷或裂纹的失稳扩展引起的。有时，在裂缝的平衡 状态达到失稳的临界状态以前还会出现缓慢的准静态亚临界扩展，最后达到临界状态使 裂纹高速传播引起最终断裂。这样，强度科学不仅要通过阻止屈服以达到高强度，而且 要通过阻止裂纹的扩展来达到高的断裂韧度。 断裂力学这门新的强度科学，扬弃了传统强度理论关于材料不存在缺陷的假设，承 认缺陷或裂纹存在，把构件看成连续和间断的统一体，认为裂纹的存在是不可避免的。 材料在生产过程中（冶炼、铸造、锻造、焊接、热处理），使用过程中（装配、摩擦损 伤、腐蚀、疲劳、中子照射、氢渗入)都会使材料产生裂纹，裂纹尖端附近的局部强度 已上升为主要矛盾。这些在传统连续介质力学中是作为次要因素被抹杀了的。 断裂力学是固体力学中研究带裂纹材料强度的学科。它着眼于裂纹尖端局部地区的

1 第一章 线弹性断裂力学基础 1.1 引 言 断裂力学是近半个世纪以来发展起来的一门新学科。它主要研究带裂纹固体的强度 和裂纹传播的规律。对于不同条件下的不同材料，人们往往根据自己的目的，将材料抽 象为某种“理想物质”以反映某些最重要的特性。在研究断裂问题时，将材料抽象为理 想线弹性体就是线弹性断裂力学。如果再考虑裂纹尖端塑性区就有弹塑性断裂力学。不 少情况下，温度的影响和“时间效应”都不能忽略。从流变学观点出发考虑到材料的流 变性能就有流变断裂学，它还可以细分为粘弹性断裂力学，粘弹塑性断裂力学，热粘弹 性断裂力学，热粘弹塑性断裂力学等。目前只有线弹性断裂力学发展比较成熟，并已制 定出规范（例如美国机械工程师协会 ASEM，锅炉与压力容器规范等）。编成手册应用 于生产上。 断裂力学涉及内容很广，这里只介绍一些基础性的内容。中国有句古话：“吃一堑， 长一智”。吃一次亏，出来一门新学科。断裂力学可以说是人类吃了大亏，从总结惨痛 血的教训中产生的。生产推动了科学发展，科学反过来又促进生产以更高的速度向前发 展。在这个过程中，旧的问题不断解决，新的矛盾又不断产生。最初，人们为了提高材 料的强度防止脆断，制成了钢材等塑性材料。进一步提高塑性材料的强度是通过阻止屈 服（阻止位错运动）来实现的。再进一步提高强度就出现了新的矛盾，强度高了，韧度 却低了，构件常在应力不高，甚至低于屈服极限的情况下发生突然的脆性破坏。如焊接 铁桥的突然倒塌，焊接轮船的脆性破坏，各种球罐的突然爆炸等等，均不能用传统的建 立在连续性假设基础上的强度科学（如材料力学）来解释。随着生产的发展，大量采用 新材料（高强度钢、复合材料、塑料）新工艺，新的工作条件（高温、高速、高压、低 温）等，致使古典强度科学无法适应新的生产水平的需要。对低应力脆断事故进行大量 分析研究表明脆性断裂是由于宏观缺陷或裂纹的失稳扩展引起的。有时，在裂缝的平衡 状态达到失稳的临界状态以前还会出现缓慢的准静态亚临界扩展，最后达到临界状态使 裂纹高速传播引起最终断裂。这样，强度科学不仅要通过阻止屈服以达到高强度，而且 要通过阻止裂纹的扩展来达到高的断裂韧度。 断裂力学这门新的强度科学，扬弃了传统强度理论关于材料不存在缺陷的假设，承 认缺陷或裂纹存在，把构件看成连续和间断的统一体，认为裂纹的存在是不可避免的。 材料在生产过程中（冶炼、铸造、锻造、焊接、热处理），使用过程中（装配、摩擦损 伤、腐蚀、疲劳、中子照射、氢渗入）都会使材料产生裂纹，裂纹尖端附近的局部强度 已上升为主要矛盾。这些在传统连续介质力学中是作为次要因素被抹杀了的。 断裂力学是固体力学中研究带裂纹材料强度的学科。它着眼于裂纹尖端局部地区的

断裂力学讲义 应力、位移场来研究带裂纹构件所承受的载荷和断裂韧度及裂纹尺寸间的定量关系，研 究裂纹扩展的规律。考察裂纹对结构强度和使用寿命的影响，建立断裂判据。提出容许 裂纹的设计方法，探讨如何控制和防止结构断裂破坏的措施。 早在1920年Griffith0为了解释玻璃、陶瓷等脆性材料的实际强度与理论强度的重 大差异，就已经建立了裂纹扩展的能量判据。在经典能量平衡方程中加入了表面能这一 项，它成功地说明了实际强度与最大裂纹尺寸之间的关系，而这一点是通常材料力学观 点无法解释的。 Gfth当年研究了下述问题：设在单位厚度板沿y轴方向均匀作用着σ使弹性伸长 后的两端固定以隔绝外界能源。实验指出，当应力σ达到临界值σ。，裂纹开始扩展，增 加其自由表面。问题是如何求出。。，即确定什么条件下裂纹会失稳而自动扩展。 b>>a b>a 裂纹的面积：2a 裂纹的表面积：4a 图1-1 Griffith带裂纹单位厚度板 可以这样来考虑问题，设想一个无裂纹的板受均匀应力σ拉伸，然后将两端固定， 此时板单位面积内的弹性应变能为 (1-1) E为Young氏模量。再设想沿Ox轴方向割开2a长的裂纹，由于裂纹表面应力的消失裂 口弹性张开消耗一部分能量以形成新裂纹表面。设有裂纹后的应变能变为U,则可算出 弹性应变能释放为 U。=U。-U=o2a3-πo24 (1-2) E 4E 裂纹是由其中心对称地向两端扩展。面积为A的裂纹上下两个表面能为 U、=2Ay (1-3) Y,为单位自由表面的表面能，简称单位表面能。 2

断裂力学讲义 2 应力、位移场来研究带裂纹构件所承受的载荷和断裂韧度及裂纹尺寸间的定量关系，研 究裂纹扩展的规律。考察裂纹对结构强度和使用寿命的影响，建立断裂判据。提出容许 裂纹的设计方法，探讨如何控制和防止结构断裂破坏的措施。 早在 1920 年 Griffith[1] 为了解释玻璃、陶瓷等脆性材料的实际强度与理论强度的重 大差异，就已经建立了裂纹扩展的能量判据。在经典能量平衡方程中加入了表面能这一 项，它成功地说明了实际强度与最大裂纹尺寸之间的关系，而这一点是通常材料力学观 点无法解释的。 Griffith 当年研究了下述问题：设在单位厚度板沿 y 轴方向均匀作用着 使弹性伸长 后的两端固定以隔绝外界能源。实验指出，当应力 达到临界值 c，裂纹开始扩展，增 加其自由表面。问题是如何求出 c ，即确定什么条件下裂纹会失稳而自动扩展。 l 图 1-1 Griffith 带裂纹单位厚度板 可以这样来考虑问题，设想一个无裂纹的板受均匀应力 拉伸，然后将两端固定， 此时板单位面积内的弹性应变能为 E U 2 2 1 2 0     (1-1) E 为 Young 氏模量。再设想沿 Ox 轴方向割开 2a 长的裂纹，由于裂纹表面应力的消失裂 口弹性张开消耗一部分能量以形成新裂纹表面。设有裂纹后的应变能变为 U，则可算出 弹性应变能释放为 E A E a U U U 4 2 2 2 2 e 0       (1-2) 裂纹是由其中心对称地向两端扩展。面积为 A 的裂纹上下两个表面能为 s s U  2A (1-3) s  为单位自由表面的表面能，简称单位表面能

第一章线弹性断裂力学基础 为了求得临界条件，下面设裂纹虚拟扩展δ。，有三种情况： OU:U., 裂纹处于非扩展状态： 0A 0A U.BU. 裂纹处于失稳状态： 6A 0A G=业_=27，临界状态。 0A 0A 式中G称为能量释放率，或称裂纹扩展力。由(1-1)、(1-2)式还可见在两端位移固定的情 况下，G=U./a=-U/a,因为U,不是裂纹长度的函数。依(1-2)(1-3)及上式有 0πo2A2 A 4E a2A,) (1-4) O 临界状态的应力为。。，依上式有 a (1-5) 1=V2/π，平面应力 1=V2/π1-v2】,平面应变 Griffith的裂纹失稳扩展条件如下 G22y,或020 (1-6) 长期以来被认为只适用于玻璃等脆性材料的Griffith理论直到50年代由Irwin☑) -Orowar]捡起，加以修正用于金属材料的脆性断裂，成为断裂韧度概念的基础。他们 认为Gth的能量平衡中必须同时考虑裂纹尖端附近塑性变形耗用的能量。裂纹扩展 时能量释放不但用于形成新的表面，对于塑性金属材料来说还要用于支付裂纹扩展前产 生塑性变形的能量，以，+y,代替y,得 E(Ys+Yp) 0。=入 EYp (1-7) a a Y,为裂纹扩展每单位面积时所消耗的塑性变形能，y。远大于y,。今后将把表面能理解 为“有效单位表面能”y,它代表裂纹扩展单位面积所需的不可逆功，并将G的临界值记 为G。=2y，临界条件写为 G=Ge (1-8) 1955年和1957年Iwin4又指出，能量观点相当于一种应力强度观点，当表示裂纹 尖端应力场强弱度的应力强度因子达到其临界值（即材料的断裂韧度）时，裂纹便失稳 扩展。脆性断裂基本上是在线弹性状态下发生的，不少情况下运用线弹性理论分析脆性 断裂能给出比较满意的结果，但当裂纹尖端附近的塑性区不能忽略不计或者与粘弹性有

第一章 线弹性断裂力学基础 3 为了求得临界条件，下面设裂纹虚拟扩展 a ，有三种情况： A U A U      e s ，裂纹处于非扩展状态； A U A U      e s ，裂纹处于失稳状态； s e s  2       A U A U G ，临界状态。 式中 G 称为能量释放率，或称裂纹扩展力。由(1-1)、(1-2)式还可见在两端位移固定的情 况下，G  Ue a   U a，因为U0不是裂纹长度的函数。依(1-2)、(1-3)及上式有  s 2 2 2 4   A E A A A             (1-4) 临界状态的应力为 c ，依上式有 a E a E s s c 2        (1-5)   2  ，平面应力 2 [ 1( )] 2     ，平面应变 Griffith 的裂纹失稳扩展条件如下 2 s G   ，或   c (1-6) 长期以来被认为只适用于玻璃等脆性材料的 Griffith 理论直到 50 年代由 Irwin[2] –Orowan[3]捡起，加以修正用于金属材料的脆性断裂，成为断裂韧度概念的基础。他们 认为 Griffith 的能量平衡中必须同时考虑裂纹尖端附近塑性变形耗用的能量。裂纹扩展 时能量释放不但用于形成新的表面，对于塑性金属材料来说还要用于支付裂纹扩展前产 生塑性变形的能量，以 s p    代替 s  得 a E a E s p p c ( )          (1-7) p  为裂纹扩展每单位面积时所消耗的塑性变形能， p  远大于 s  。今后将把表面能理解 为“有效单位表面能” ，它代表裂纹扩展单位面积所需的不可逆功，并将 G 的临界值记 为 2 Gc  ，临界条件写为 G  Gc (1-8) 1955 年和 1957 年 Irwin[4]又指出，能量观点相当于一种应力强度观点，当表示裂纹 尖端应力场强弱度的应力强度因子达到其临界值（即材料的断裂韧度）时，裂纹便失稳 扩展。脆性断裂基本上是在线弹性状态下发生的，不少情况下运用线弹性理论分析脆性 断裂能给出比较满意的结果，但当裂纹尖端附近的塑性区不能忽略不计或者与粘弹性有

断裂力学讲义 关的时间效应不能忽略不计时，线弹性断裂力学的应用就受到了限制。那时就要用到下 面两章将要讨论的弹塑性断裂力学及流变断裂学。在本章中，我们认为裂纹体是理想线 弹性体，问题归结为含裂纹体的线弹性力学分析。 1.2裂纹前沿的应力、位移场 1.2.1 Westergaard方法 Gi笛th理论是从整体平衡得到的，但由于未分析裂纹前沿的应力、位移场，因而未 能从细节上弄清。根据裂纹面的受力变形方式，可将裂纹分为三种类型：I型（张开型）、 Ⅱ型（滑开型）、Ⅱ型（撕开型），撕开型也称反平面剪切型。 I型张开型 Ⅱ型滑开型 型撕开型 图1-2裂纹的三种类型 I、Ⅱ型裂纹问题属于平面问题。平面应力和平面应变是平面问题中的两种基本状态。 利用表l-2改变E(Young氏模量)和y(Poisson比)，可以使两种状态公式互换从而统 地进行处理。 表1-1平面问题的两种状态 平面应力 平面应变 0:=T=tg=0 O:=v(Ox+0,) E:=-v(o,+a)/E 8.=0 各应力、应变及位移分量均不是z的函数 表1-2平面问题里两种状态的公式互换 平面应力一平面应变 平面应变一平面应力 y→v/1-y) v→y/(1+v) E→E/1-v2) E→E1+2y/1+y)2 剪切模量4不变 4

断裂力学讲义 4 关的时间效应不能忽略不计时，线弹性断裂力学的应用就受到了限制。那时就要用到下 面两章将要讨论的弹塑性断裂力学及流变断裂学。在本章中，我们认为裂纹体是理想线 弹性体，问题归结为含裂纹体的线弹性力学分析。 1.2 裂纹前沿的应力、位移场 1.2.1 Westergaard 方法 Griffith 理论是从整体平衡得到的，但由于未分析裂纹前沿的应力、位移场，因而未 能从细节上弄清。根据裂纹面的受力变形方式，可将裂纹分为三种类型：I 型（张开型）、 II 型（滑开型）、III 型（撕开型），撕开型也称反平面剪切型。 I 型 张开型 II 型 滑开型 III 型 撕开型 图 1-2 裂纹的三种类型 I、II 型裂纹问题属于平面问题。平面应力和平面应变是平面问题中的两种基本状态。 利用表 1-2 改变 E（Young 氏模量）和 （Poisson 比），可以使两种状态公式互换从而统 一地进行处理。 表 1-1 平面问题的两种状态 平面应力 平面应变  z  xz  yz  0 ( )  z   x   y  z   ( x   y ) E  0 z  各应力、应变及位移分量均不是 z 的函数 表 1-2 平面问题里两种状态的公式互换 平面应力→平面应变 平面应变→平面应力   1(  )   1(  ) 1( ) 2 E  E  2 E  E 1(  2 ) 1(  ) 剪切模量  不变

第一章线弹性断裂力学基础 Ⅲ型裂纹问题是反平面应变状态。平面应变状态的位移发生在y平面内，位移分 量为：≠0，v≠0，"=0，而反平面应变状态的位移发生在垂直于y的平面中，位 移分量为：u=0,v=0,w≠0。 不考虑体积力时，单连通域平面弹性理论问题归结为求应力函数Φ使得④满足双调 和方程) 、>22币_✉4本=里+2，+2史-0 axdyoy (1-9) 及具体问题的边界条件。复连通域还要满足位移单值条件。求得应力函数Φ后，可依下 式计算各应力分量 a2Φ 2Φ a2Φ 0x= 0,=02, Txy=- (1-10) Oxoy 式中Φ称为Aiy应力函数。不难直接验证，若f(i=l,2,3)均是调和函数，即 Vf- o" =0 (1-11) 则它们与x,y的线性组合 Φ=f+f2+f (1-12) 是双调和函数，即它们满足式(1-9)。 应力函数用复变函数表示时可用来解决许多裂纹问题。若复变函数Z(z)=ReZ+ilmZ, 在某区域上处处可导，则称Z(z)为该区域上的解析函数。设复变量：=x+y的函数为复 变解析函数，则其导数和积分仍为解析函数。复变解析函数的实部和虚部都是调和函数， 且满足Cauchy-Riemann条件： OReZ_0lmZ=Re dz dy z (1-13) ImZ ReZ .=Im dZ Ox y d= 设x(z)、p(z)为解析函数，令f=Rex(z),f2=Rep(z)和f3=Imp(z),可将(1-l2) 写成如下形式6 Φ=Re[Ep(z)+(] (1-14) Irwin(1957)引用Westergaardl应力函数(1939)建立了裂纹尖端奇异应力场。设Z(z)为 复变解析函数并采用以下记号 Z=Z.Z-Z.Z=Z (1-15) dz dz dz

第一章 线弹性断裂力学基础 5 III 型裂纹问题是反平面应变状态。平面应变状态的位移发生在 xy 平面内，位移分 量为：u  0 ，v  0， w  0，而反平面应变状态的位移发生在垂直于 xy 的平面中，位 移分量为：u  0，v  0， w  0 。 不考虑体积力时，单连通域平面弹性理论问题归结为求应力函数Φ使得Φ满足双调 和方程[5] 2 0 4 4 2 2 4 4 4 2 2 4                y Φ x y Φ x Φ Φ Φ (1-9) 及具体问题的边界条件。复连通域还要满足位移单值条件。求得应力函数Φ后，可依下 式计算各应力分量 2 2 y Φ x     ， 2 2 x Φ y     ， x y Φ xy      2  (1-10) 式中Φ称为 Airy 应力函数。不难直接验证，若 fi (i  )3,2,1 均是调和函数，即 0 2 2 2 2 2                i  i f x y f (1-11) 则它们与 x ， y 的线性组合 1 2 3 Φ f  xf  yf (1-12) 是双调和函数，即它们满足式(1-9)。 应力函数用复变函数表示时可用来解决许多裂纹问题。若复变函数 Z(z)=ReZ+iImZ， 在某区域上处处可导，则称 Z(z)为该区域上的解析函数。设复变量 z  x  iy 的函数为复 变解析函数，则其导数和积分仍为解析函数。复变解析函数的实部和虚部都是调和函数， 且满足 Cauchy-Riemann 条件：                     z Z y Z x Z z Z y Z x Z d d Im Im Re d d Re Re Im (1-13) 设 (z)、(z)为解析函数，令 Re ( ) 1f   z ， Re ( ) 2 f   z 和 Im ( ) 3f   z ，可将(1-12) 写成如下形式[6] Φ Re[z(z)  (z)] (1-14) Irwin[4](1957)引用 Westergaard[7]应力函数(1939)建立了裂纹尖端奇异应力场。设 Z(z)为 复变解析函数并采用以下记号 Z z Z  d d ， Z z Z  d d ， Z z Z   d d (1-15)

断裂力学讲义 1.2.1.11型裂纹 Westergaard选用如下的重为应力函数： 重=ReZ,+ylmZ (1-16) 式中下标1表示I型裂纹。由于(1-16)具有(1-12)的形式，它显然自动满足双调和方程(1-9)， 依(1-10)各应力分量为 o,=ReZ-yImZi ,Re Z+yIm Z (1-17) Tx=-yReZi 对任何解析函数Z()都可得到依上式所确定的应力，问题归结为寻求一个解析函数 Z(:),同时满足考虑问题的边界条件，为了求得位移分量，只须将应(1-17)代入物理 关系及应变位移关系（几何关系）即可。以平面应变状态为例，将(1-17)代入平面应变 状态条件下的物理关系 8,=E0-vo,-v0+v)o,】 (1-18) 6,=E0-2)o,-v1+v)o,】 及几何关系 (1-19) 并积分得 -+[1-2v)ReZ-ylmZ u= E (1-20) v=1+V[2(-v)ImZ,-yReZ E 作为Westergaard方法应用的例子，现讨论带中心穿透裂纹并受均匀双轴拉应力的 无限大板的裂纹尖端应力、位移场。当坐标原点选在裂纹中点时，选取复应力函数 Z(:)-0-a (1-21) 就能满足问题的全部条件 (I)在y=0,-a<x<a处，o,=0,t=0: (2)在z→0,0x=0,=0,tg=0 由于Z(e)除(-a<x<a,y=0)以外是解析函数，又满足问题的边界条件，从而是 问题的解。为了计算裂缝尖端附近的应力、位移场，将坐标原点移至裂纹右尖端处。令 6

断裂力学讲义 6 1.2.1.1 I 型裂纹 Westergaard 选用如下的Φ为应力函数： I I I Φ  ReZ  y ImZ (1-16) 式中下标 I表示 I型裂纹。由于(1-16)具有(1-12)的形式，它显然自动满足双调和方程(1-9)， 依(1-10)各应力分量为               I I I I I Re Re Im Re Im y Z Z y Z Z y Z xy y x    (1-17) 对任何解析函数 ( ) I Z z 都可得到依上式所确定的应力，问题归结为寻求一个解析函数 ( ) I Z z ，同时满足考虑问题的边界条件，为了求得位移分量，只须将应力(1-17)代入物理 关系及应变-位移关系（几何关系）即可。以平面应变状态为例，将(1-17)代入平面应变 状态条件下的物理关系                [(1 ) 1( ) ] 1 [(1 ) 1( ) ] 1 2 2 y y x x x y E E             (1-18) 及几何关系 x u x     ， y v y     ， y u x v xy        (1-19) 并积分得                I I I I 1(2[ )Im Re 1 [(1 2 )Re Im 1 Z y Z E v Z y Z E u     (1-20) 作为 Westergaard 方法应用的例子，现讨论带中心穿透裂纹并受均匀双轴拉应力的 无限大板的裂纹尖端应力、位移场。当坐标原点选在裂纹中点时，选取复应力函数 2 2 I ( ) z a z Z z    (1-21) 就能满足问题的全部条件 (1) 在 y  0， a  x  a 处， y  0， xy  0 ； (2) 在 z   ， x   y   ， xy  0 由于 ( ) I Z z 除（  a  x  a ， y  0）以外是解析函数，又满足问题的边界条件，从而是 问题的解。为了计算裂缝尖端附近的应力、位移场，将坐标原点移至裂纹右尖端处。令

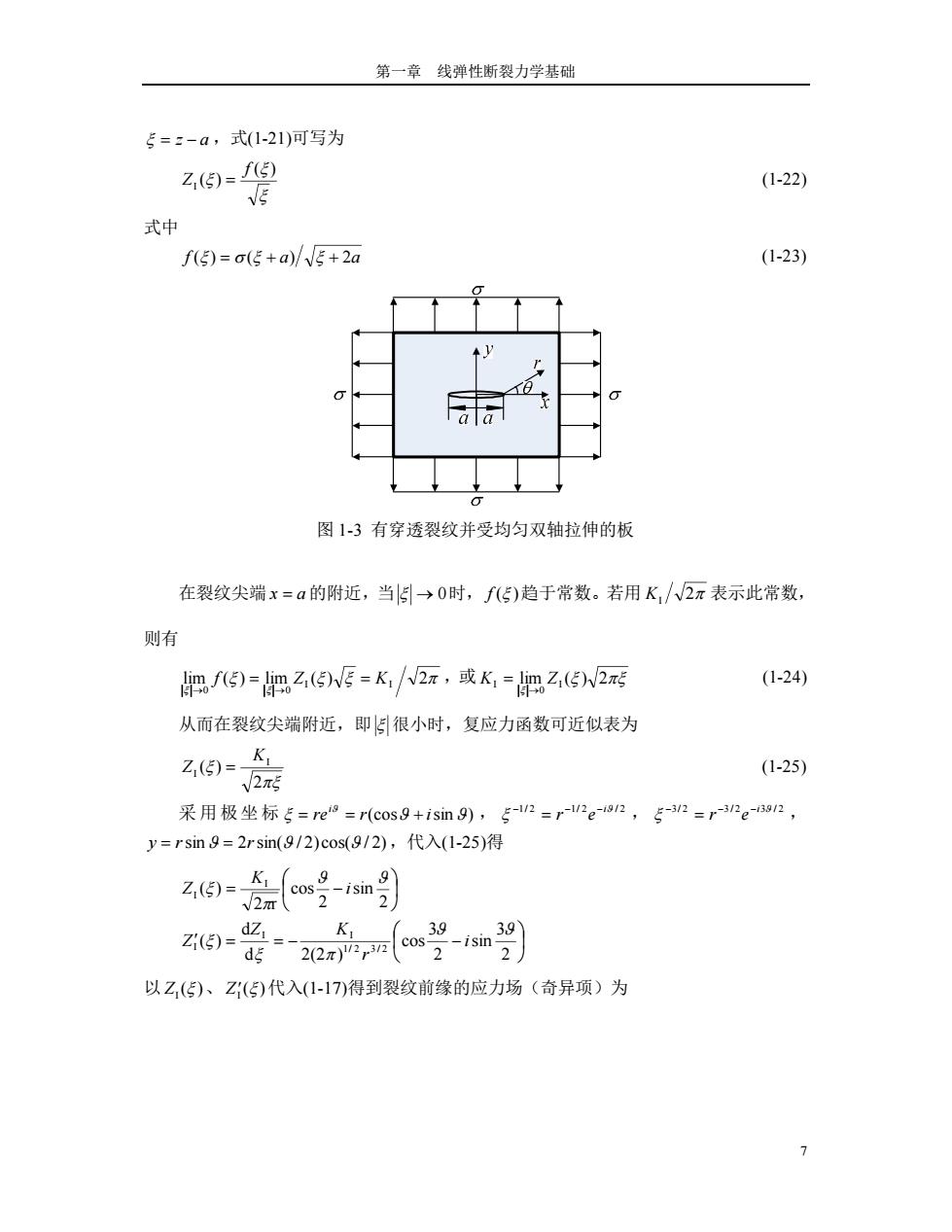
第一章线弹性断裂力学基础 5=z-a,式(1-21)可写为 Z,⑤)=但 (1-22) 式中 f5)=o(5+a)/V5+2a (1-23) aa 图1-3有穿透裂纹并受均匀双轴拉伸的板 在裂纹尖端x=a的附近，当5→0时，f5)趋于常数。若用K,/W2π表示此常数， 则有 f5)=Z店=K/2x,或K,=肥Z(52 (1-24) 从而在裂纹尖端附近，即很小时，复应力函数可近似表为 份高 (1-25) 采用极坐标=e8=r(cos9+isin9),5-2=r-12e-i812，专-312=r3/2e392, y=rsin9=2rsin(9/2)cos(9/2),代入(1-25)得 Z,(5)= 9 v2m 2 2 Z1(5) d☑=- 39 39 2(2π)'232 2 以Z,(5)、Z(5)代入(1-17)得到裂纹前缘的应力场（奇异项）为 >

第一章 线弹性断裂力学基础 7   z  a ，式(1-21)可写为    ( ) ( ) I f Z  (1-22) 式中 f ( )   (  a)   2a (1-23) 图 1-3 有穿透裂纹并受均匀双轴拉伸的板 在裂纹尖端 x  a 的附近，当   0时， f ( )趋于常数。若用 KI 2 表示此常数， 则有       lim ( ) lim ( ) 2 I I 0 0 f  Z  K   ，或    lim ( ) 2 I 0 KI Z   (1-24) 从而在裂纹尖端附近，即  很小时，复应力函数可近似表为   2 ( ) I I K Z  (1-25) 采 用 极 坐 标  (cos sin)  re r i i    ， 2/1 /1 2  2/  i r e     ， 2/3 2/3 3 2/  i r e     ， y  rsin  2rsin( )2/ cos( )2/ ，代入(1-25)得                    2 3 sin 2 3 cos d 2(2 ) d ( ) 2 sin 2 cos 2 r ( ) /1 2 2/3 I I I I I          i r Z K Z i K Z 以 ( ) I Z  、 ( ) I Z  代入(1-17)得到裂纹前缘的应力场（奇异项）为

断裂力学讲义 0x= 1-sinsin 9 39 √2m 2 2 2 K 9 9 39 0y= 1+sin- sin (1-26) V2 2 2 2 K,sin号cos 9 9 39 Tx=- cos 2 对于平面应力问题，有o:=0:对于平面应变问题，有o:=(o.+o,)。式中K称为应 力强度因子，它表示了应力场的强弱程度。K,由(1-24)确定 K=Z,传2店= o(5+a）\2π形=oVa (1-27) -0V5(5+2a 以(1-25)代入式(1-20)并注意到 E=2u(1+v) 得到平面应变情况下裂纹尖端的位移场 u=KL V2 cos1-2v+sin 2 (1-28) -osg 或将平面应力、平面应变两种情况写成统一形式 u=K V2π (1-29) 式中 (3-)/1+v),平面应力 k= (1-30) 3-4 平面应变 值得注意的是基于有穿透裂纹并受均匀双轴拉伸这种特殊情况所得到的上述Ⅰ型裂 纹尖端附近的应力、位移场具有普遍的意义，即对于其他几何情况（如有限尺寸、中心 裂纹、边裂纹)、受力情况（如非均匀受力、集中力）的I型裂纹，裂纹尖端场的表达 式也是相同的，只要裂纹尖端附近的裂纹面上不受面力作用，所不同的只是应力强度因 子，因此，对于特定的结构只要确定K,就可以了。对于Ⅱ、Ⅲ型裂纹尖端也有类似的 结论，各种情况下的应力强度因子可查有关手册8，)。用类似方法可求Ⅱ、Ⅱ型裂纹尖 端场。 8

断裂力学讲义 8                           2 3 cos 2 cos 2 sin 2 2 3 sin 2 1 sin 2 cos 2 2 3 sin 2 1 sin 2 cos 2 I I I                r K r K r K xy y x (1-26) 对于平面应力问题，有  0  z ；对于平面应变问题，有 ( )  z   x  y 。式中 KI 称为应 力强度因子，它表示了应力场的强弱程度。 KI 由(1-24)确定 a a a K Z                   2 ( 2 ) ( ) lim ( ) 2 lim 0 I 0 I (1-27) 以(1-25)代入式(1-20)并注意到 E  2 1(  )          2 sin 2 cos 2 2 2 2 I I I      i r K K Z 得到平面应变情况下裂纹尖端的位移场                          2 2 2 cos 2 sin 2 2 1 2 sin 2 cos 2 I 2 I 2           K r v K r u (1-28) 或将平面应力、平面应变两种情况写成统一形式                          2 ( )1 cos 2 1 2 sin 2 2 ( )1 sin 2 1 2 cos 2 I 2 I 2         k K r v k K r u (1-29) 式中        平面应变 平面应力 3 4 , 3( ) 1( ),    k (1-30) 值得注意的是基于有穿透裂纹并受均匀双轴拉伸这种特殊情况所得到的上述 I 型裂 纹尖端附近的应力、位移场具有普遍的意义，即对于其他几何情况（如有限尺寸、中心 裂纹、边裂纹）、受力情况（如非均匀受力、集中力）的 I 型裂纹，裂纹尖端场的表达 式也是相同的，只要裂纹尖端附近的裂纹面上不受面力作用，所不同的只是应力强度因 子，因此，对于特定的结构只要确定 KI 就可以了。对于 II、III 型裂纹尖端也有类似的 结论，各种情况下的应力强度因子可查有关手册[8,9]。用类似方法可求 II、III 型裂纹尖 端场

第一章线弹性断裂力学基础 1.2.1.1Ⅱ型裂纹 对于Ⅱ型（滑开型）裂纹，可取如下的应力函数 重=-yReZ (1-31) 由(1-10)及(1-18)、(1-19)可求得各应力分量及平面应变情况下位移分量 o,=2ImZn+yRe Zi y=-yReZi Txy ReZu-yIm Zi (1-32) u=+v[2(1-v)imZn+yReZn =栏0-2eZ.-ym21 对于含有长2a穿透裂纹的无限大板，在受纯剪切时，可选用如下形式的解析函数 Zn=ty-a (1-33) 作为复应力函数，则满足全部边界条件。在裂纹尖端附近有Z1=K/√2π5，相应的应 力及位移分量如下 图1-4有穿透裂纹并受均匀平面内剪切的无限大板 39 0x=- Knsin 2+cos-cos √2m 2 2 2 9 9 39 0y= Kusin号cos7co (1-34) √2m 2 2 9 9 39 tw-2m 2 1-sin sin 2 对于平面应力问题，有o.=0;对于平面应变问题，有o.=v(o+o,)。 9

第一章 线弹性断裂力学基础 9 1.2.1.1 II 型裂纹 对于 II 型（滑开型）裂纹，可取如下的应力函数 II ReZII Φ  y (1-31) 由(1-10)及(1-18)、(1-19)可求得各应力分量及平面应变情况下位移分量 [ 1( 2 )Re Im ] 1 1(2[ )Im Re 1 Re Im Re 2Im Re II II II II II II II II II Z y Z E v Z y Z E u Z y Z y Z Z y Z xy y x                          (1-32) 对于含有长 2a穿透裂纹的无限大板，在受纯剪切时，可选用如下形式的解析函数 2 2 II z a z Z    (1-33) 作为复应力函数，则满足全部边界条件。在裂纹尖端附近有 ZII  KII 2 ，相应的应 力及位移分量如下 2a y x 图 1-4 有穿透裂纹并受均匀平面内剪切的无限大板                            2 3 sin 2 1 sin 2 cos 2 2 3 cos 2 cos 2 sin 2 2 3 cos 2 2 cos 2 sin 2 II II II                r K r K r K xy y x (1-34) 对于平面应力问题，有  0  z ；对于平面应变问题，有 ( )  z   x  y

断裂力学讲义 u=Ksm 9 4V2π (1-35) P= Kn r 9 9 V2π cos -(1-2v)+sin2 2 2 或将平面应力、平面应变两种情况写成统一形式 u=K,sing .91 k+1)+cos2 9 4V2π 2L2 2 (1-36) v-- 220-)+sn2 9「1 9 K,为Ⅱ型裂纹的应力强度因子 r5+a0)V2π形=ta Ka(2a) (1-37) 1.2.3.3Ⅱ型裂紋 Ⅲ型裂纹属于反平面应变问题。”=v=0,w≠0，位移垂直于y平面，对于反平 面应变问题，其基本公式为 几何方程：y=- ’y= Ow (1-38) 1 1 物理方程：Ye (1-39) 平衡方程： r=+a=-0 (1-40) ox dy 由(1-38)和(1-40)式得 72w=0 (1-41) w=LImZm (1-42) Y 代入(1-38)、(1-39)式并注意到amZ/ax=mZ,aImZ/ay=ReZ,得 Ts=ImZm (1-43) Tx=ReZm 对于含有长为2a的穿透裂纹的无限大板，在无限远处作用有剪应力t=π时，可 选复应力函数为 Zm=ty-a (1-44) 10

断裂力学讲义 10                           2 1( 2 ) sin 2 cos 2 2 2 2 cos 2 sin 2 II 2 II 2           K r v K r u (1-35) 或将平面应力、平面应变两种情况写成统一形式                          2 1( ) sin 2 1 2 cos 2 2 ( )1 cos 2 1 2 sin 2 II 2 II 2         k K r v k K r u (1-36) KII 为 II 型裂纹的应力强度因子 a a a K Z                   2 ( 2 ) ( ) lim ( ) 2 lim 0. II 0 II (1-37) 1.2.3.3 III 型裂纹 III 型裂纹属于反平面应变问题。u  v  0 ，w  0 ，位移垂直于 xy 平面，对于反平 面应变问题，其基本公式为 几何方程： x w xz     ， y w yz     (1-38) 物理方程： xz xz    1  ， yz yz    1  (1-39) 平衡方程：  0      x y xz yz   (1-40) 由(1-38)和(1-40)式得 0 2  w  (1-41) III Im 1 w Z   (1-42) 代入(1-38)、(1-39)式并注意到 ImZ x  ImZ ， ImZ y  Re Z ，得      III III Re Im Z Z yz xz   (1-43) 对于含有长为 2a的穿透裂纹的无限大板，在无限远处作用有剪应力   yz 时，可 选复应力函数为 2 2 III z a z Z    (1-44)