
时代教育·国外高校优秀教材精选 (原书第2版) 结构理论 Theory of Structures (美) S.P.铁木辛柯(S.P.Timoshenko) D.H.杨(D.H.Young) 著 叶红玲杨庆生等译 Mc 机械工业出版社 Graw Education CHINA MACHINE PRESS Hill

序 像铁木辛柯独著或同他人合著的其他的力学教科书一样,初版于1945年、 再版于1965年的《结构理论》也是一部经典著作。 经典的魅力在于,它的光芒不但不会随年华的流逝而衰减,相反会时时给 人以新的照耀。这本《结构理论》作为经典教科书,不仅在于它仍然可以用作土 木类专业的教材或参考书,还对于其他专业研读变形体力学的人员给予更多 启发。 结构理论或结构力学同材料力学一样,都属于变形体力学的早期发展,学 习这门课程的意义是多方面的。首先是力学概念的突破,即由不变形体(质点与 刚体)向变形体(弹性体、塑性体、流体等)的升华。如果不是在变形上寻找出路, 力学永远也不会走出构件或结构的单纯靠力平衡方程无法求解的困境。 无论超静定的构件或结构,如果不进行受力变形的几何协调方程的研究, 就不可能由柳暗走向花明。紧接着变形的研究,必然呼唤对于力与变形(或应力 与应变)本构关系的探讨。结构理论的意义就在于把材料力学对构件使用成功的 “平衡一变形一本构”三要点的方法论,在结构上作进一步林漓尽致的发挥和 发展。 学习结构理论的另一个意义在于它的工程实用性,铁木辛柯与杨的这本教 材充分体现了理论密切联系实际的特点,对于我们从事实实在在的工程结构分 析与设计,不仅有直接使用价值,也颇有理念上的深刻启发性。 当今,力学等领域发展的各种数值计算方法均可为工程结构分析乃至优化 设计提供有效的服务。从现在的观点看,材料力学实际是关于杆件的变形体力 学,结构力学则是杆件体系的变形体力学。如果说二者都是研究天然有限元的 变形体力学,那么,有限元方法则是从天然有限元(轴力杆、梁等)向人造有限元 (膜、板、壳、块体等)变形体力学的延伸。 从这个角度来看铁木辛柯与杨的《结构理论》,可以看到这本书是颇有前瞻 性的。本书在1965年的再版序言里特别强调了结构分析的矩阵法和动载荷计 算。话虽简练,却很有远见。 从1945年出版第1版到1965年出版第2版的20年间,力学取得了很多重 大进展,为工程和其他学科作出了很大的贡献。其中,在那个时期出现的有限

结构理论 元方法就以矩阵法为重要工具。无论结构分析的矩阵法还是动力分析,从1965 年以后又有了巨大的发展。至今又过去了将近40年,包括有限元方法在内的各 种数值计算方法已经获得了广泛的应用,达到了无论科学还是技术须臾都不能 离开它们的境界。 不难想象,从1945年到现在的近60年间,这本书为工程界和力学界人才的 培养,在结构力学方面作出了极其重要的贡献,因此有理由相信,这本翻译书 将为中国相关专业的大学生们提供一本有益的参考书。 也许伴随着计算机技术的不断发展和使用,今后结构理论教材的内容会有 更多的取舍和重组,但是基本的原理非但不会减弱,反而还会进一步加强,例 如矩阵法、动力分析、能量原理和方法,会对其进行重点阐发。同时,工程的 直觉和力学的概念也要更加突出。因此,经典著作会放射出永不泯灭的光芒。 隋允康 写于北京工业大学 装 的

译者序 由铁木辛柯(S.P.Timoshenko)教授和杨(D.H.Young)教授合著的《结构理论》(1965年, 第2版),作为一本工科结构力学教科书,在世界范围内得到广泛的推崇和认可。面世半个 多世纪以来,已经惠及几代读者,被多次以各种语言和版式印制,已经成为本领域内一部名 副其实的经典著作。在科学技术飞速发展的今天,愈发显示出它的独特价值。我们相信,本 书中文版的问世,将会对读者正确理解和掌握结构力学的知识有所帮助;同时,对我国结构 力学教学和科研工作起到借鉴作用。 原书是为工程专业的本科生和一年级研究生编写的一本教材。作者之一一铁木辛柯教授 是一位特别注重解决工程实际问题的力学专家。本书通篇贾穿了理论联系实际、注重工程应用 的学术思想;在保持内容完整性和知识系统性的前提下,特别关注工程实际问题的处理。本书 用大量的篇幅介绍工程问题的模型化和各种分析方法。例如,对于工程中经常通到的结构形式 和载荷状况如何建模、如何选取适当的分析方法以及对计算结果的检验和判断等问题,都进行 了详细的讨论。对于结构力学问题的各种研究方法,通过实例详细介绍了分析步骤,并由特殊 示例归纳到一般原理,这非常有利于读者特别是初学者学习和掌握本课程的核心知识。 本书主要内容酒盖了桁架、刚架、拱和连续梁等结构形式的静力学和动力学。阐述了各 种结构在静定和超静定状态下的内力、变形和影响线的分析方法和能量原理;介绍了结构动 力学的基础知识和结构理论的最新发展,特别是对当时刚刚萌芽的计算机分析方法给予了特 别关注。本书的知识体系与沿袭至今的结构力学教材基本一致。 本书的编写体系以研究问题的类型为主线展开,根据知识本身的内在联系划分章节,由 浅入深,逻辑性强,推理缜密。这样可避免学生陷入学习的死角—一只注意方法本身的按步 推算,忽略对研究问题的整体把握。作为大学教材,本书的内容编排非常符合循序渐进的学 习规律;也适合于包括在校大学生和工程技术人员在内的读者作为自学教材。 本书在翻译时,删除了原书第4章关于空间桁架和第11章桥梁结构分析的内容(本书的 第4、5、6、7、8、9章,为原书的第5、6、7、8、9、10章;第10章为原书的第12章。), 因为前者的处理方法与平面桁架基本一致;而后者已经发展成为专门的学科。力和长度等物 理量译稿采用了原书中所使用的符号以及英制单位,为了方便读者阅读,我们在书后附加了 英制单位与国际单位的换算表。 本书译者分工如下:第1章、第2章、第6章、第7章、第8章、第10章和附录由叶 红玲译;前言、第3章、第4章、第5章、第9章由杨庆生译。全部译稿由杨庆生和叶红玲 采用互译互校的方法共同校对。隋允康教授为本书翻译撰写了序。研究生李智健、白海波、 许芳、王海明、李春江、刘君等参加了文稿的初译,在此一并表示衷心感谢。 由于时间仓促和译者水平的限制,书中可能存在一些不足之处,欢迎广大读者批评指正。 译者 于北京工业大学

原著前言 这是《结构理论》的第2版,和第1版一样,它主要是作为土木工程大学生 和一年级研究生的结构分析课程的教村。为达到这个目的,本书非常注重各类 结构的分析方法与其基本原理的紧密联系。只有深入地理解这些基本原理,工 程师才能成功地将分析方法应用于他们在现代社会面临的经常变化的问题。 本书大略地分为两部分:第1部分处理静定结构;第2部分处理超静定结 构。按此安排,前4章依次处理静力学基础(主要是几何静力学)、静定平面析 架、梁与桁架的影响线、静定空间桁架。接下来,第5章和第6章处理弹性系 统相关的基本定理及其在梁、桁架位移计算上的应用。再下面的几章依次处理 超静定桁架、拱和刚架的分析。最后几章介绍结构分析的矩阵法、筋条悬索桥 分析和结构动力学。 在第2版中,前7章基本和第1版保持一致。关于拱和刚架的第8章和第9 章则完全重写。基于最小功定理和弹性中心的概念,现在对拱的处理已经简化。 加入了使用弹性中心概念分析门式刚架的若干文献。在重写的章节,关于连续 梁和刚架分析的斜率一挠度方程的使用已经扩展到非等截面构件系统,并给出 许多例题。 自从本书首次问世(1945年)以来,结构分析的两个方面变得非常重要,即 公式表示的矩阵方法和动力载荷作用下的结构分析。它们都是非常宽泛的课题, 有许多现成的书籍可以参考。这里的第10章和第12章仅是这些课题的介绍, 但是我们希望这能鼓励读者在这些方向上继续研究。 致谢(略) S.P.Timoshenko D.H.Young 8远

目 录 序 3.6三较拱的影响线………84 译者序 3.7简单析架的影响线…… 87 原著前言 3.8复合析架的影响线………… 91 第1章平面静力学基础…1 第4章弹性体的一般原理…95 1.1平面汇交力系 4.1拉伸、扭转和弯曲的应变能…95 1.2三力平衡 ……………3 4.2登加原理…………97 1.3平衡方程…… 4.3广义形式的应变能… 100 1.4内力…………8 4.4卡氏(Castigliano)第一定理…103 1.5索多边形…12 4.5卡氏(Castigliano)第二定理…106 1.6索多边形的应用…………15 4.6最小功原理……110 1.7分布力作用下的索曲线…18 4.7互等定理 …………………114 1.8柔性悬索……………21 第5章较接桁架的挠度计算…120 1.9弯矩图……25 1.10虚位移原理……… 29 5.1卡氏(Castigliano)定理的应用…120 5.2挠度计算的麦克斯韦一莫尔 第2章静定平面桁架…33 (Maxwell--Mohr)法…123 2.1简单折架…………33 5.3图解法求析架位移…125 2.2反力……35 5.4虚载荷法……131 2.3结点法…38 5.5变异的虚载荷法……135 2.4麦克斯韦(Maxwell)图 40 第6章超静定铰接桁架 ………141 2.5截面法…………43 2.6组合析架………48 6.1概述……141 2.7平面析架的一般理论…52 6.2带一个冗余杆件的析架 …143 2.8复杂析架:亨尼勃格(Henneberg) 6.3带多个冗余杆件的析架 ……147 方法…56 64超静定析架中的装配应力和 2.9虚位移法……60 温度应力 …151 6.5超静定桁架的影响线 …155 第3章影响线 …64 6.6超静定空间结构…159 3.1移动载荷和影响线…64 第7章拱与刚架 ……164 3.2梁支座反力的影响线…68 3.3剪力影响线……72 7.1概述…164 3.4弯矩影响线…76 7.2对称二较拱…165 3.5带有横梁的主梁…80 7.3对称无较拱…169

结构理论 7.4无铰刚架…175 9.4连续梁的矩阵分析…253 7.5有较刚架 …………181 9.5拱和刚架的矩阵方法 …259 7.6温度变化和支座沉降的影响…183 9.6连续刚架的矩阵分析 …264 7.7环…………186 第10章结构动力学…269 第8章连续梁与刚架 …189 10.1单自由度系统的自由振动…269 8.1斜率一挠度方程…189 10.2瑞雷(Rayleigh)法 …273 8.2固端梁… 192 10.3稳态强迫振动…277 8.3连续梁 195 10.4一个干扰力的通用情况…281 8.4变戴面梁… 199 10.5数值积分…… 285 8.5变戴面连续梁………… 205 10.6图形积分……… 289 8.6带等截面杆的简单刚架 212 10.7轨道静动应力… 294 8.7带等栽面杆的连续刚架… 219 10.8等截面梁的横向振动…298 8.8力矩分配法…225 附录 … 302 8.9建筑物刚架分析… 231 8.10带非等戴面杆的刚架…234 附录A国际单位制单位与英美制 单位换算表…302 第9章结构分析的矩阵法…239 附录B习题答素… 304 9.1力法和位移法…239 附录C人名对照表…311 9.2矩阵代数基础…… 241 附录D关键词索引…312 9.3矩阵方法在平面析架中的应用…246 后 装 的

第1章 平面静力学基础 1.1平面汇交力系 结构理论以静力学理论为基础。在本书中,我们认为读者已经熟悉静力学理论,但是因 为静力学理论在分析工程结构问题上的重要作用,还是要复习和回顾一下在工程结构分析中 非常有用的部分静力学原理。首先是力的平行四边形原理:P,和P2两个力,如图1.1a中 的矢量OA和OB,可以合成为一个合力R,合力由以这两个力为边构成的平行四边形的对角 线确定,如图中矢量0C。同样,合力也可以通过力三角形得到,如图1.1b所示。图1.1b 中三角形ABC与图1.1a中的三角形OAC是等同的。 如果平面上的几个力作用在同一点O(见图1.2a),总可以合成为过该点的一个合力。 这个合力可以通过连续应用力平行四边形法则(见图1.2a)确定,或者通过力多边形的闭合 边来确定(见图1.2b)。 图1.1 图1.2 如果力多边形是闭合的,那么合力为零,即给定力系平衡。因此,如果平面汇交力系是 平衡的,则它们的自由矢量组成的力多边形必是闭合的。 上述图形的平衡条件在结构分析中是非常有用的。 举一个简单的例子。如图1.3a所示,一重W的重物受绳索的拉力作用。选环0为自由 体,则环O在W、S,和S2三个力的作用下达到平衡。力S,和S2的方向沿着绳索,它们的 大小称为轴力或拉力。如果重力W的大小已知,则拉力S,和S2的大小可以由图1.3b所示 的封闭的力三角形得到:S,=Wcsca和S2=Wcota
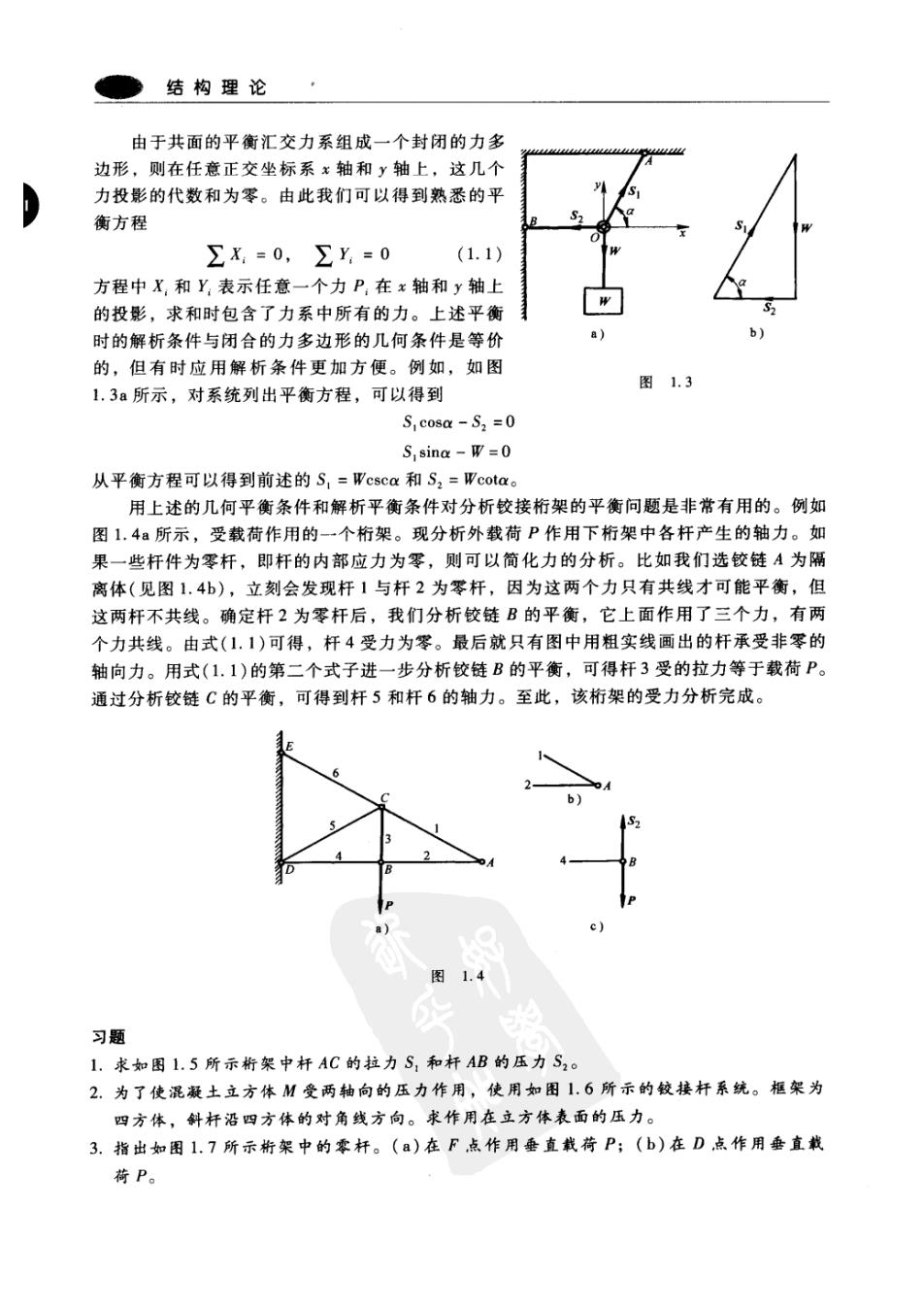
结构理论 由于共面的平衡汇交力系组成一个封闭的力多 边形,则在任意正交坐标系x轴和y轴上,这几个 力投影的代数和为零。由此我们可以得到熟悉的平 衡方程 ∑X=0,∑y=0 (1.1) 方程中X,和Y:表示任意一个力P,在x轴和y轴上 的投影,求和时包含了力系中所有的力。上述平衡 时的解析条件与闭合的力多边形的几何条件是等价 a) 的,但有时应用解析条件更加方便。例如,如图 图1.3 1.3a所示,对系统列出平衡方程,可以得到 S cosa-S2=0 S sina-W=0 从平衡方程可以得到前述的S,=Wesca和S2=Wcota。 用上述的几何平衡条件和解析平衡条件对分析铰接桁架的平衡问题是非常有用的。例如 图1.4所示,受载荷作用的一个桁架。现分析外载荷P作用下桁架中各杆产生的轴力。如 果一些杆件为零杆,即杆的内部应力为零,则可以简化力的分析。比如我们选铰链A为隔 离体(见图1.4b),立刻会发现杆1与杆2为零杆,因为这两个力只有共线才可能平衡,但 这两杆不共线。确定杆2为零杆后,我们分析铰链B的平衡,它上面作用了三个力,有两 个力共线。由式(1.1)可得,杆4受力为零。最后就只有图中用粗实线画出的杆承受非零的 轴向力。用式(1.1)的第二个式子进一步分析铰链B的平衡,可得杆3受的拉力等于载荷P。 通过分析铰链C的平衡,可得到杆5和杆6的轴力。至此,该桁架的受力分析完成。 图1.4 习题 1.求如图1.5所示析架中杆AC的拉力S,和杆AB的压力S2。 2.为了使混凝土立方体M受两轴向的压力作用,使用如图1.6所示的较接杆系统。框架为 四方体,斜杆沿四方体的对角线方向。求作用在立方体表面的压力。 3.指出如图1.7所示析架中的零杆。(a)在F点作用垂直载荷P;(b)在D点作用垂直戴 荷P

第1章平面静力学基础 4.如图1.8所示,将对角线的方向由AD改为BC,则简单析架的作用力有何影响? 5.用实线画出两个简支析架中的主动杆件,戴荷如图1.9所示。 图 1.5 图 1.6 图 1.1 图1.9 1.2三力平衡 同一平面上三个相互不平行的力只有汇交于一点才能处于平衡状态。为证明这个结论, 参考图1.10,力P和Q为汇交于一点0的任意两个力,那么第三个力S与这两个力平衡的 条件是它与这两个力的合力R是大小相等、方向相反且作用在同一条直线上。当然,合力R 必汇交于点O。因此,力S也必过汇交点O。 上述的三力汇交定理对于求解在已知力作用下,刚体 或结构在支座处的约束反力是非常有用的。例如,起重机 如图1.11所示,柱AB由轴承A和B支撑,以使起重机能 绕着垂直轴旋转。在垂直载荷P的作用下,起重机在轴承 A和B处施加压力,而在起重机的支座处产生了大小相 等、方向相反的力作用在起重机上。因此,垂直力P同反 力R,和R。是三力平衡的。忽略在轴承B处的摩擦,反力 图1.10