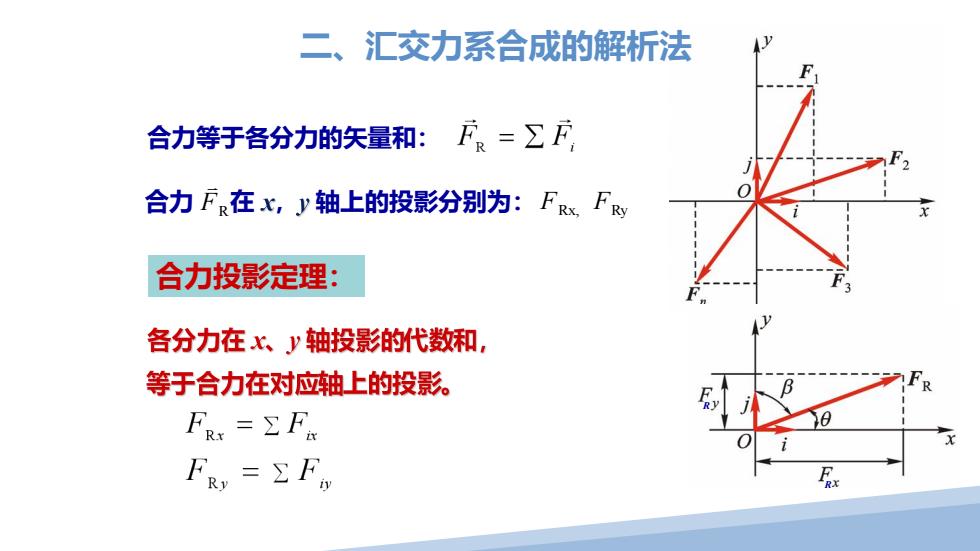
二、汇交力系合成的解析法 合力等于各分力的矢量和:F=∑F 合力F在X,y轴上的投影分别为:FRx.FRy 合力投影定理: 各分力在太、y轴投影的代数和, 等于合力在对应轴上的投影。 FRx=∑F FR,=∑F
合力 F R在 , 轴上的投影分别为: FRx, FRy 合力等于各分力的矢量和: 合力投影定理: R R 二、汇交力系合成的解析法
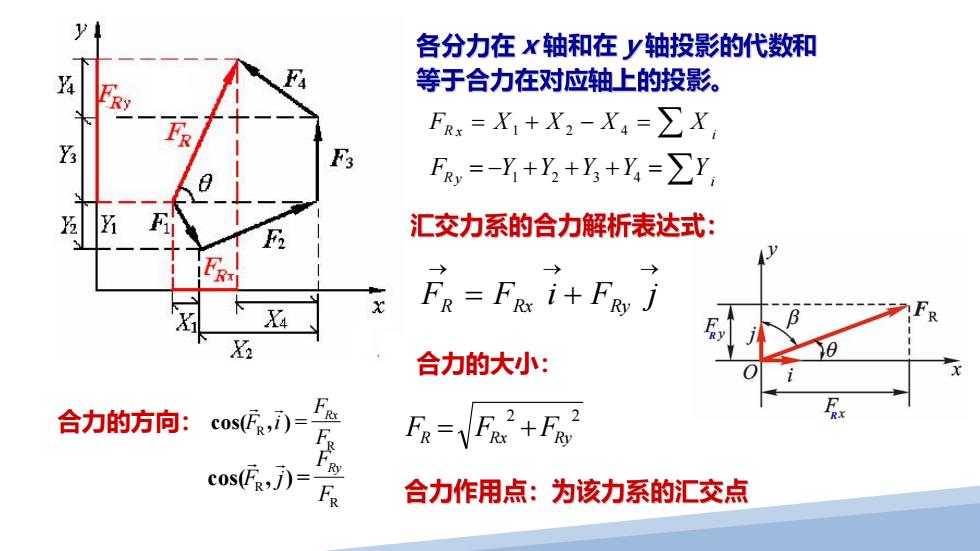
各分力在x轴和在y轴投影的代数和 a 等于合力在对应轴上的投影。 FRx=X1+X2-X4=∑X, Fs F,=-Y+y2+y+Y4=∑Y, 汇交力系的合力解析表达式: Fg=Fg i+Fgy j X2 合力的大小: 合力的方向: cos(1)-Fa cos(F,j)= 合力作用点:为该力系的汇交点
R R F F i F j R Rx Ry 2 2 FR FRx FRy R x i F X1 X 2 X 4 X R y i F Y1 Y2 Y3 Y4 Y 合力的大小: 合力的方向: R R = F F F i Rx cos( , ) R R = F F F j Ry cos( , )

[例 已知:图示平面共点力系,F=200NF=300N F3=100NF,=250N 求:此力系的合力。 60 解:用解析法 F=>F=Fcos30-F.cos60-Fcos45+Fcos45=129.3N F=>F=Fsin30+Fsin60-Fsin45-F sin45=1123N F=VF+F=171.3N c0s0=F=0.7548 COs B=- =0.6556 F 0=40.99°,B=49.01
解:用解析法 求:此力系的合力。 [例] 已知:图示平面共点力系,F1 = 200N F2 300N F3 100N F4 250N