华南农业大学：《工程力学》课程教学资源（课件讲稿）第3章 力偶理论 3.1 力对点之矩、汇交力系的合力矩定理

第3章力偶理论 §3.1 力对点之矩汇交力系的合力矩定理

§3.1 力对点之矩 汇交力系的合力矩定理 第3章 力偶理论

一、 力对点之矩汇交力系的合力矩定理 力对物体可以产生 移动效应-取决于力的大小、方向 转动效应一取决于力矩的大小、方向 扭矩扳手 力矩：是度量力对刚体转动效应强弱的物理量

一 、力对点之矩 汇交力系的合力矩定理

一、力对点之矩汇交力系的合力矩定理 1、平面力系中力对点的矩 B, M。F)表示力F绕O转动的效应 A MoF=±Fd 力矩的单位：Nm或kNm d一力臂 0一矩心 正负号规定： 力使物体绕矩心逆时针转为+ 力使物体绕矩心顺时针转为一

A B F Mo(F)表示力F 绕 O 转动的效应 力矩的单位: N·m 或 kN·m Mo(F) =±Fd O d d —力臂 O —矩心 正负号规定： 力使物体绕矩心逆时针转为 + 力使物体绕矩心顺时针转为 – 一、力对点之矩 汇交力系的合力矩定理

一、力对点之矩汇交力系的合力矩定理 几个结论： B 1)若F=0或d=0,则：MF=0 2)当力F沿其作用线滑动时，力对同一点 的矩MF)不变。 3)同一个力对不同点的矩不同，即：力对 点的矩与矩心的选择有关。 4)MF=±Fd=±2OAB面积 注意：平面力系中力对点的矩是一代数量

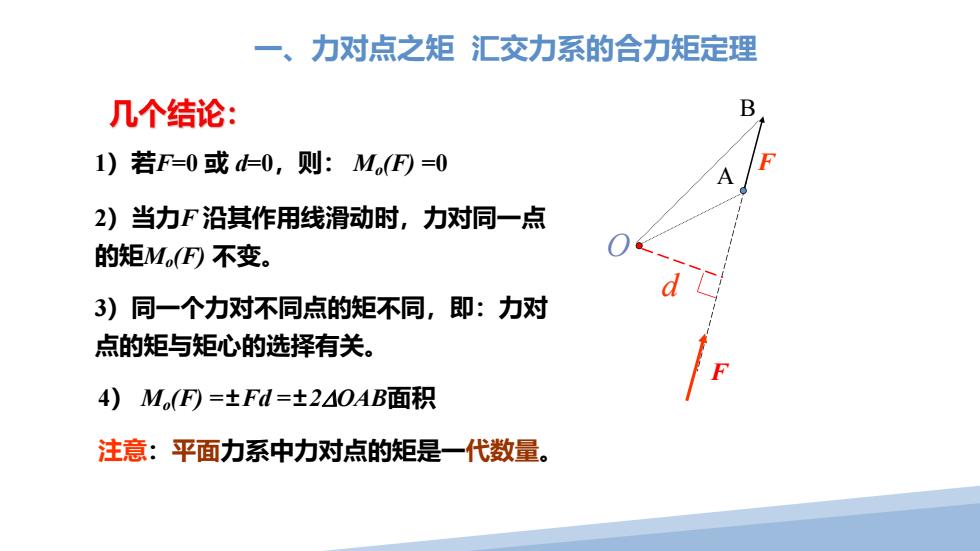
A B F d O 1）若F=0 或 d=0，则： Mo(F) =0 2）当力F 沿其作用线滑动时，力对同一点 的矩Mo(F) 不变。 3）同一个力对不同点的矩不同，即：力对 点的矩与矩心的选择有关。 4） Mo(F) =±Fd =±2OAB面积 注意：平面力系中力对点的矩是一代数量。 一、力对点之矩 汇交力系的合力矩定理 F

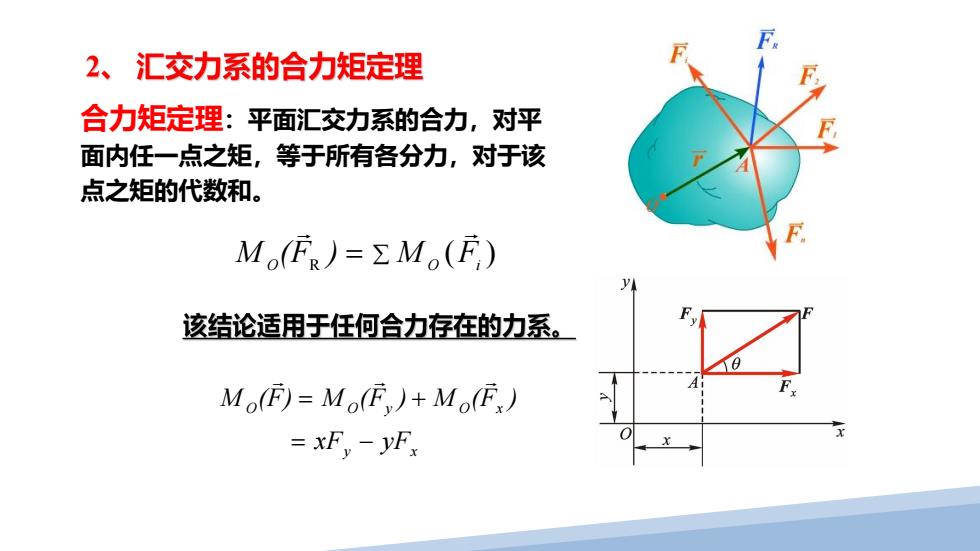
2、汇交力系的合力矩定理 合力矩定理：平面汇交力系的合力，对平 面内任一点之矩，等于所有各分力，对于该 点之矩的代数和。 MF)=ΣM(F) 该结论适用于任何合力存在的力系。 Mo(F)=Mo(F)+Mo(F.) =xF,-yF

合力矩定理：平面汇交力系的合力，对平 面内任一点之矩，等于所有各分力，对于该 点之矩的代数和。 ( ) O R M O Fi M (F )     y x O O y O x xF yF M (F) M (F ) M (F )       

【例1】 已知：F=1400N, 0=20°，r=60mm 求：Mo(F) 解：直接按定义 M (F=F.h=F.r.cose =78.93N.m 按合力矩定理 M)=M(匠)+M(匠) =F.cos0.r=78.93N.m

直接按定义 按合力矩定理 【例1】 求: 已知: F  1400N, M (F) O  解: θ  20 , r  60mm  Mo F F h   F rcos  78.93N m       Mo F Mo Ft Mo Fr       F cos r  78.93N m