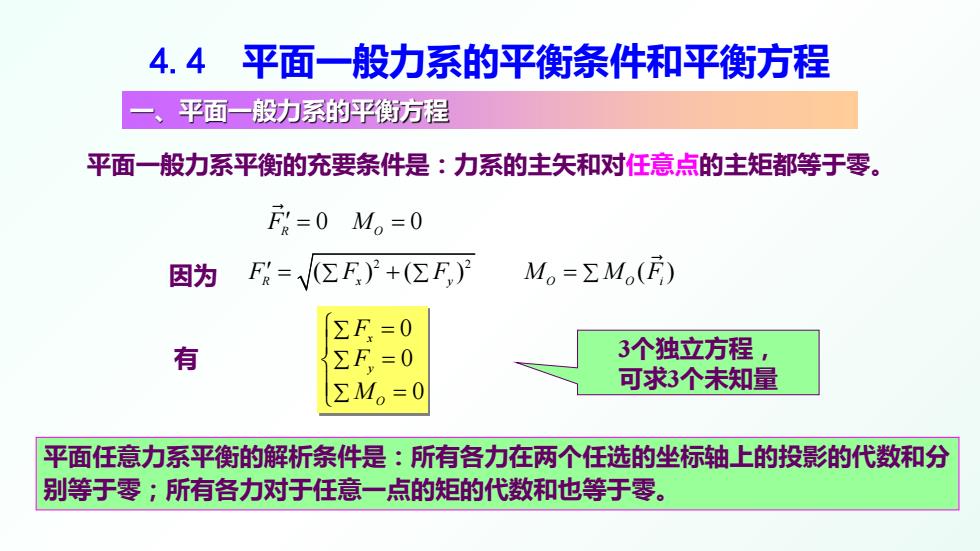
4.4平面一般力系的平衡条件和平衡方程 平面一般力系的平衡方程 平面一般力系平衡的充要条件是:力系的主矢和对任意点的主矩都等于零。 F=0M。=0 因为F=V区F)+(区E) M。=ΣMo() ∑F=0 有 ΣF=0 3个独立方程, ∑M。=0 可求3个未知量 平面任意力系平衡的解析条件是:所有各力在两个任选的坐标轴上的投影的代数和分 别等于零;所有各力对于任意一点的矩的代数和也等于零
4.4 平面一般力系的平衡条件和平衡方程 平面一般力系平衡的充要条件是:力系的主矢和对任意点的主矩都等于零。 因为 有 0 0 F M R O ′ = = 2 2 ( ) ( ) ( ) F F F M MF R x y ∑∑ ∑ O Oi ′ =+ = 0 0 0 x y O F F M ∑ ∑ ∑ = = = 一、平面一般力系的平衡方程 平面任意力系平衡的解析条件是:所有各力在两个任选的坐标轴上的投影的代数和分 别等于零;所有各力对于任意一点的矩的代数和也等于零。 3个独立方程, 可求3个未知量
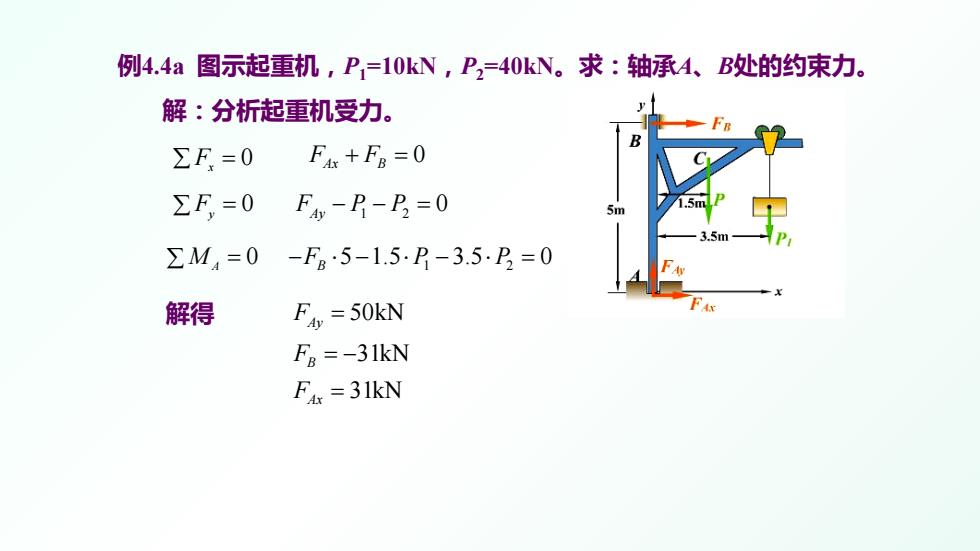
例4.4a图示起重机,P=10kN,P,=40kN。求:轴承A、B处的约束力。 解:分析起重机受力。 ∑F=0 Fis+FB=0 ΣF=0F--B=0 ∑M4=0-F。5-1.5·P-3.5.D=0 解得 F=50kN F=-31kN Fi =31kN
例4.4a 图示起重机,P1=10kN,P2=40kN。求:轴承A、B处的约束力。 解:分析起重机受力。 解得 0 F F Ax B + = 1 2 0 F PP Ay −− = 1 2 5 1.5 3.5 0 − ⋅− ⋅ − ⋅ = F PP B 0 ∑ F x = 0 ∑ F y = 0 ∑ M A = 50kN 31kN 31kN Ay B Ax F F F = = − =
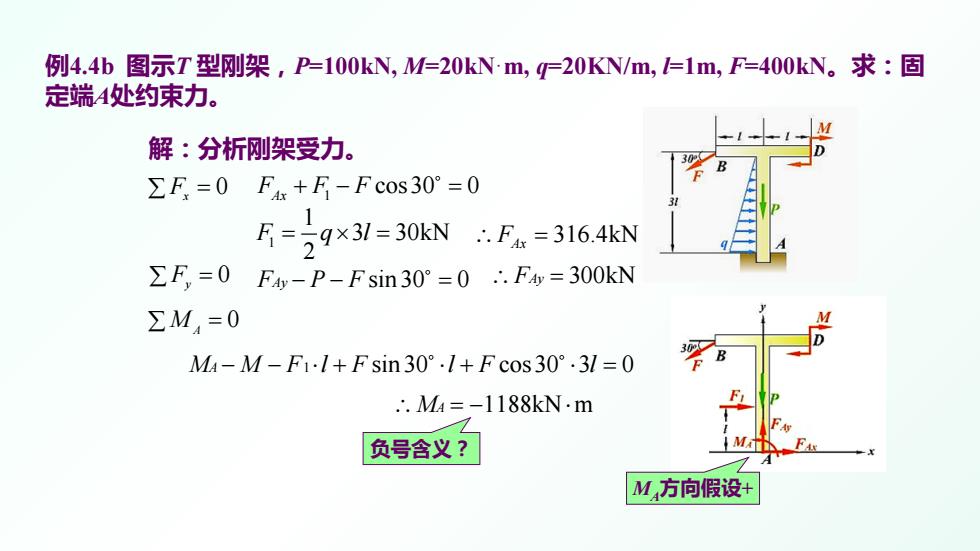
例4.4b图示T型刚架,P-=100kN,M=20kNm,=20KN/m,I=1m,F-=400kN。求:固 定端4处约束力。 解:分析刚架受力。 ∑F=0F+F-Fcos30°=0 F=29×31=30kNF=3164kN ∑F,=0F4-P-Fsin30°=0.Fay=300kN ∑M,=0 MA-M-F1-1+Fsin30°.1+Fcos30°.3l=0 ∴.M4=-1188kN.m 负号含义? M,方向假设+
例4.4b 图示T 型刚架,P=100kN, M=20kN·m, q=20KN/m, l=1m, F=400kN。求:固 定端A处约束力。 解:分析刚架受力。 0 ∑ F x = 1 1 3 30kN 2 F ql = ×= 1 cos30 0 F FF Ax +− = ∴ = FAx 316.4kN 0 ∑ F y = 0 ∑ M A = F PF Ay −− = sin 30 0 ∴ = FAy 300kN M M Fl F l F l A − − ⋅+ ⋅+ ⋅ = 1 sin 30 cos30 3 0 ∴ =− ⋅ MA 1188kN m 负号含义? MA方向假设+
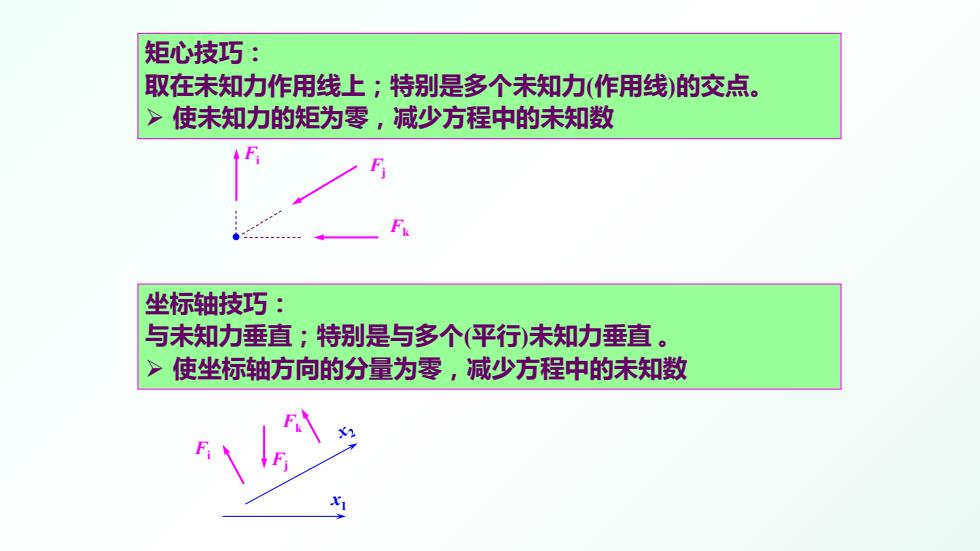
矩心技巧: 取在未知力作用线上:特别是多个未知力(作用线)的交点。 >使未知力的矩为零,减少方程中的未知数 坐标轴技巧: 与未知力垂直;特别是与多个(平行)未知力垂直。 >使坐标轴方向的分量为零,减少方程中的未知数
矩心技巧: 取在未知力作用线上;特别是多个未知力(作用线)的交点。 使未知力的矩为零,减少方程中的未知数 坐标轴技巧: 与未知力垂直;特别是与多个(平行)未知力垂直 。 使坐标轴方向的分量为零,减少方程中的未知数 Fi Fj Fk Fi Fj Fk x1
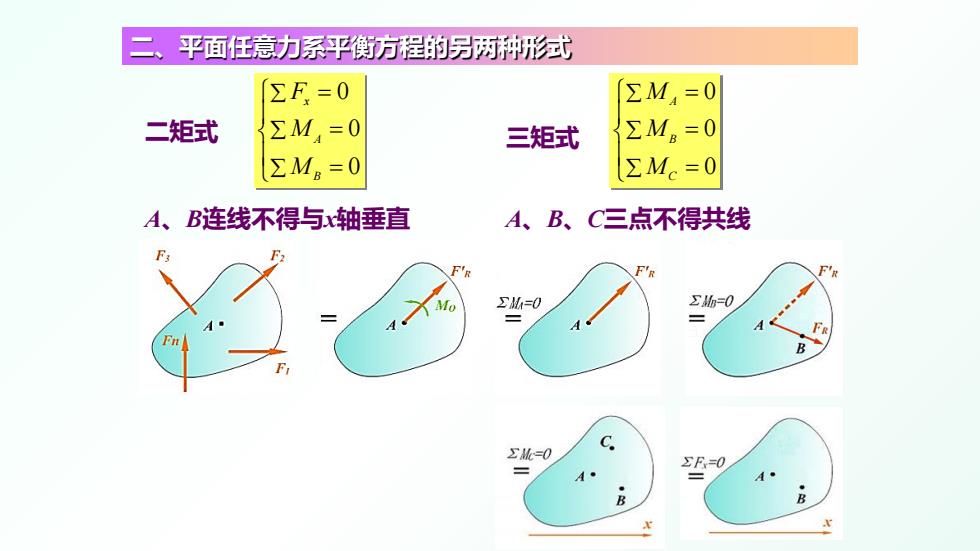
二 平面任意力系平衡方程的房两种形式 ΣF=0 ΣM,=0 二矩式 ∑M,=0 三矩式 ∑Ma=0 ∑M。=0 ΣMc=0 A、B连线不得与轴垂直 A、B、C三点不得共线 F 卫M=0 Σ胎=0 Fn ΣM=0 C F=0 B
二、平面任意力系平衡方程的另两种形式 二矩式 A、B连线不得与x轴垂直 0 0 0 x A B F M M ∑ ∑ ∑ = = = 三矩式 A、B、C三点不得共线 0 0 0 A B C M M M ∑ ∑ ∑ = = =

平面任意力系平衡方程的三种形式 ΣF=0 一般式 ΣF=0 ∑M,=0 ΣF=0 二矩式 两个取矩点,连线 ∑M,=0 不得与投影轴垂直 ∑MB=0 ΣM4=0 三矩式 ∑Mg=0 三个取矩点,不得共线 ∑M。=0 单个对像:对不同矩心、不同坐标轴可写多个方程,但独立的最多只有3个,并不 能解3个以上未知量(线性相关): 多个对像:各自有3个独立方程,总方程及未知量可>3个
平面任意力系平衡方程的三种形式 一般式 二矩式 两个取矩点,连线 不得与投影轴垂直 三矩式 三个取矩点,不得共线 0 0 0 x y A F F M ∑ ∑ ∑ = = = 0 0 0 x A B F M M ∑ ∑ ∑ = = = 0 0 0 A B C M M M ∑ ∑ ∑ = = = 单个对象:对不同矩心、不同坐标轴可写多个方程,但独立的最多只有3个,并不 能解3个以上未知量(线性相关); 多个对象:各自有3个独立方程,总方程及未知量可>3个

例4.4c已知:P1=4kN,P2=10kN,尺寸如图。 求:BC杆受力及铰链A受力。 解:取AB梁,画受力图。 ∑F=0 F-F,cos30°=0 ∑Fn=0F-P-+Fsin30°=0 (1① 30 ΣM,=0 Fsin30°.6-4P-3P=0 解得F,=17.33kNF=5.33N 比较: ∑F.=0 F-Ecos30°=0 ∑M=0 {Fsin30°.6-4P,-3P=0(2) ∑MB=0 -6F+3P+2P=0 比较: ∑M4=0 F,sin30°.6-4P-3P=0 三组 ∑MB=0 -6F+3P+2P=0 (3) 结果相同 ∑Mc=0 F·AC-3P-4P=0 入
例4.4c 已知:P1=4kN,P2=10kN,尺寸如图。 求:BC杆受力及铰链A受力。 解: 取AB 梁,画受力图。 解得 0 0 0 ix iy A F F M ∑ = ∑ = ∑ = 1 2 2 1 cos30 0 sin 30 0 (1) sin 30 6 4 3 0 Ax T Ay T T F F F PPF F PP − = −−+ = ⋅− − = F F T =17.33kN 5.33kN Ay = 比较: 比较: 0 0 0 ix A B F M M ∑ = ∑ = ∑ = 2 1 1 2 cos30 0 sin 30 6 4 3 0 (2) 6 32 0 Ax T T Ay F F F PP F PP − = ⋅− − = − ++ = 0 0 0 A B C M M M ∑ = ∑ = ∑ = 2 1 1 2 1 2 sin 30 6 4 3 0 6 3 2 0 (3) 34 0 T Ay Ax F PP F PP F AC P P ⋅− − = − ++ = ⋅ −− = 三组 结果相同!

三、平面平行力系的平衡方程 ∑F=0 0+0+0+…=0 无效 ∑F=0 ∑F=0Fcos0-Fcos0+Fcos0+…=0 等价 ∑F,=0Fsin0-E,sin0+Fsin0+…=0 ∑F=0、∑F,=0只有一个起作用,于是 平面平行力系的(独立)平衡方程为两个,有两种形式 ∑F,=0 ∑M4=0 各力不得与投影轴垂直 ∑M,=0 A、B两点连线不得与各力平行 ∑Ma=O
三、平面平行力系的平衡方程 平面平行力系的(独立)平衡方程为两个,有两种形式 各力不得与投影轴垂直 A、B两点连线不得与各力平行 0 ∑ F x = 000 0 +++ = 0 0 y A F M ∑ ∑ = = 0 0 A B M M ∑ ∑ = = 0 ∑ F x = 0 ∑ F y = 123 FFF cos cos cos 0 θθθ − + += 123 FFF sin sin sin 0 θθθ − + += ∑Fx=0 、∑Fy=0只有一个起作用,于是 0 ∑ F y = 无效 等价