
目录 CONTENTS 41 圆轴扭转时的变形 42刚度条件
目录 CONTENTS 1 2 圆轴扭转时的变形 刚度条件
圆轴扭转时的变形 dx 之前推导出 T=Glpd d0≠ d p-jdo=j0画 GIp p相对扭转角 G孔抗扭刚度 分段轴或阶梯轴: M GCc p 21
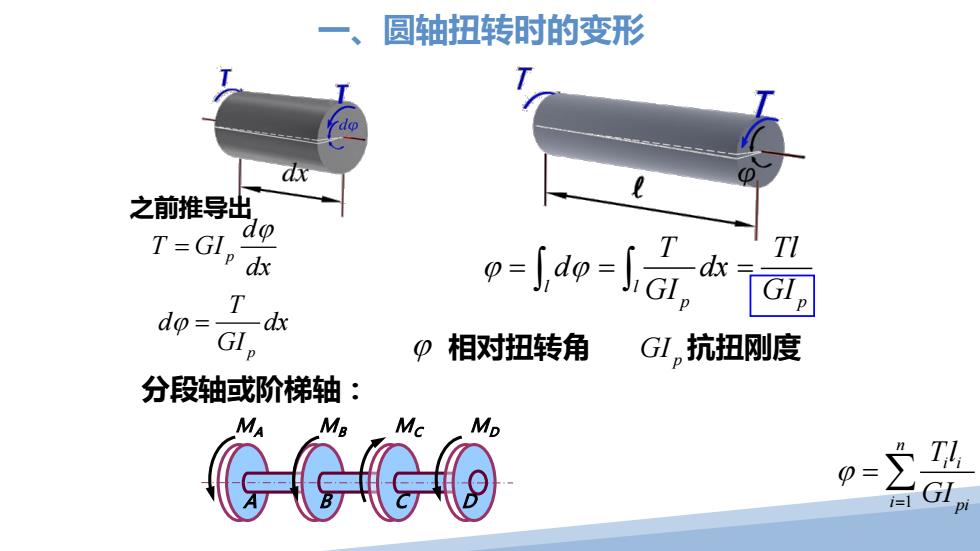
一、圆轴扭转时的变形 1 n i i i pi Tl GI ϕ = = ∑ p T d dx GI ϕ = l ϕ ϕ = d ∫ l p T dx GI = ∫ p Tl GI = ϕ 相对扭转角 GI p 抗扭刚度 分段轴或阶梯轴: MA MB MC MD A B C D p d T GI dx ϕ = 之前推导出
二、刚度条件 9'= do T dx 用0'表示变化率 do dx 称为单位长度扭转角(相当于/=1) T T180 (rad/m) (/m) GI GI 扭转则度条件一乙 s<[p] I, 许用单位长度扭转角
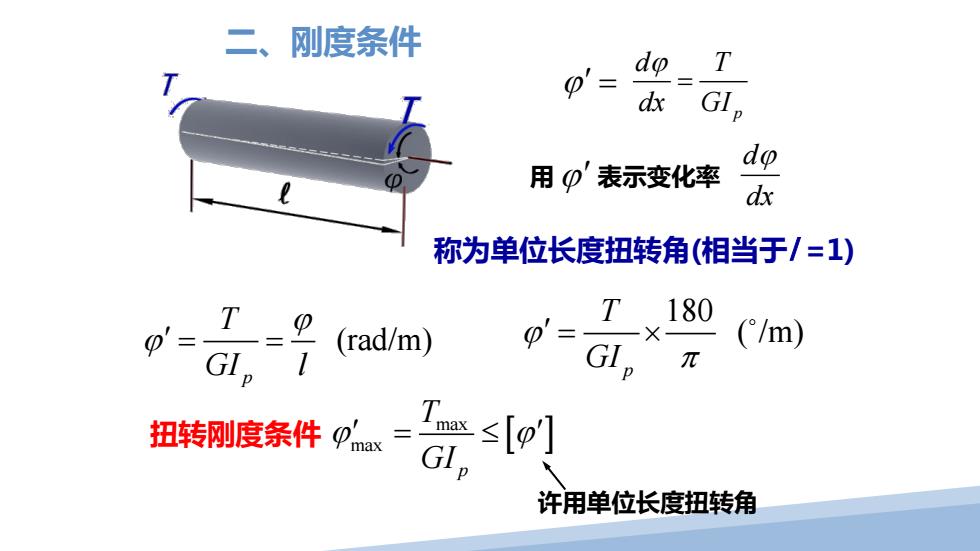
扭转刚度条件 二、刚度条件 p d T dx GI ϕ ϕ′ = = 用 ϕ ′ 表示变化率 d dx ϕ 称为单位长度扭转角(相当于l =1) (rad/m) p T GI l ϕ ϕ′ = = 180 ( /m) p T GI ϕ π ′ = × [ ] max max p T GI ϕ ϕ ′ ′ = ≤ 许用单位长度扭转角

扭转强度条件(与应力相关) T Tmax= W s(] 已知TD和[t],校核强度 πD3 已知T和[x],设计截面 W,= 16 已知D和[t],确定许可载荷 扭转刚度条件(与应变相关) 盛[p] 已知T、D和[p],校核刚度 GIp 已知T和[p],设计截面 1p= πD4 32 已知D和[0],确定许可载荷
扭转强度条件 扭转刚度条件 max [ ] t T W τ τ = ≤ 3 16 t D W π = [ ] max max p T GI ϕ ϕ ′ ′ = ≤ 4 32 p D I π = 已知 T 、D 和 [τ ],校核强度 已知 T 和 [τ ] ,设计截面 已知 D 和 [τ ] ,确定许可载荷 已知 T 和 [ϕ ′] ,设计截面 已知 T 、D 和 [ϕ ′] ,校核刚度 已知 D 和 [ϕ ′] ,确定许可载荷 (与应力相关) (与应变相关)

例1某传动轴所承受的扭矩T=200Nm,轴的直径d=40mm。材料的[x]= 40MPa,切变模量G=80GPa,许用单位长度扭转角[p]=1°/m。试校核该轴的 强度和刚度。 解:((1)校核轴的强度 TT 16×200 Tmax w, 3.14×(40×10-3)3 16 =15.9x10Pa=15.9MPa<[z] (2)校核轴的刚度 T180 T 180 32×200 180 G。 π 80×10×3.14×(40×103)43.14 32 =0.57/m<[p] 该轴满足强度和刚度条件
max t T W τ = max 180 p T GI ϕ π ′ = × < [ϕ′] 例 1 某传动轴所承受的扭矩 T = 200 N·m,轴的直径 d = 40 mm。材料的[τ ] = 40 MPa,切变模量G = 80 GPa,许用单位长度扭转角[ϕ ′] =1˚/m。试校核该轴的 强度和刚度。 3 3 3 6 16 200 3.14 (40 10 ) 16 15.9 10 Pa 15.9MPa T π d − × = = × × =× = <[τ ] 4 180 32 T d G π π = × 解:(1) 校核轴的强度 (2) 校核轴的刚度 该轴满足强度和刚度条件。 9 3 4 32 200 180 80 10 3.14 (40 10 ) 3.14 − × = × ×× ×× 0.57 /m° =
例2某传动轴设计要求转速n=500r/min,输入功率P=50kW,输出功率分 别P2=20kW及P3=30kW,已知:G=80GPa,[x]=70MPa,[p]= 1°/m,试确定: ①AB段直径D和BC段直径D2? ②若全轴选同一直径,应为多少? ③主动轮与从动轮如何安排合理? 解:①图示状态下,扭矩如图 T X N.m T7w=95495=954.90N-m) -572.9 n -954.9 Tc=95495=572.9N-m
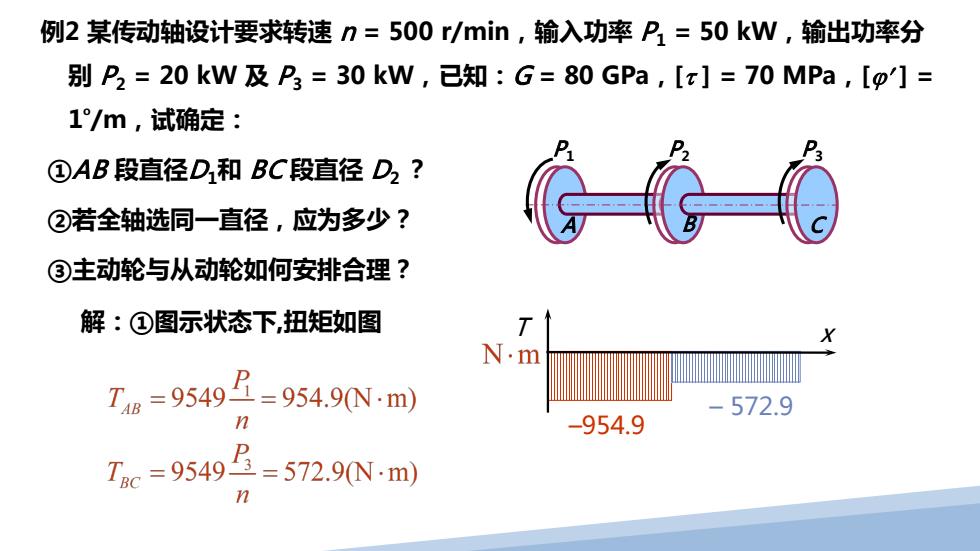
例2 某传动轴设计要求转速 n = 500 r/min,输入功率 P 1 = 50 kW,输出功率分 别 P 2 = 20 kW 及 P 3 = 30 kW,已知:G = 80 GPa,[τ ] = 70 MPa,[ϕ′ ] = 1º/m,试确定: ①AB 段直径D1和 BC 段直径 D2 ? ②若全轴选同一直径,应为多少? ③主动轮与从动轮如何安排合理? 解:①图示状态下,扭矩如图 T x –954.9 – 572.9 P 1 P 2 P 3 A B C

由强度条件得: W,= πD3 、T 16 [] 16T 16×954.9 AB段 3 41.2mm 3.14×70×106 BC段 D:z 16T, 16×572.9 =34.6mm V3.14×70×106 由刚度条件得: T 180 32G[o]π T N.m 572.9 954.9
3 16 [ ] t D T W π τ = ≥ [ ] 2 3 3 2 6 16 16 572.9 34.6 mm 3.14 70 10 T D π τ × ′ ≥= = × × [ ] 4 180 32 p D T I G π ϕ π =≥ × ′ [ ] 1 3 3 1 6 16 16 954.9 41.2 mm 3.14 70 10 T D π τ × ′ ≥= = × × 由刚度条件得: AB段 BC段 由强度条件得: P 1 P 2 P 3 A B C T x –954.9 – 572.9

由强度条件得:D'≥41.2mm D,'≥34.6mm 由刚度条件得:1,= D4 、 180 32G[p]π 32×180T 32×180×954.9 =51.4mm π2G[p] V3.142×80×109×1 32×180T 32×180×572.9 =45.2mm π2G[p] 1 3.142×80×109×1 综上,得:D≥51.4mm, D2≥45.2mm ②若全轴选同一直径时 D≥51.4mm
2 4 4 2 2 2 9 32 180 32 180 572.9 45.2 mm [ ] 3.14 80 10 1 T D π ϕ G × × × ′′ ≥= = ′ ×× × 1 4 4 1 2 2 9 32 180 32 180 954.9 51.4 mm [ ] 3.14 80 10 1 T D π ϕ G × × × ′′ ≥= = ′ ×× × 1 2 综上,得: D D ≥ ≥ 51.4 mm , 45.2 mm ②若全轴选同一直径时 D ≥ 51.4 mm 2 由强度条件得: D1 ′ ≥ 41.2 mm D ′ ≥ 34.6 mm 由刚度条件得: [ ] 4 180 32 p D T I G π ϕ π =≥ × ′
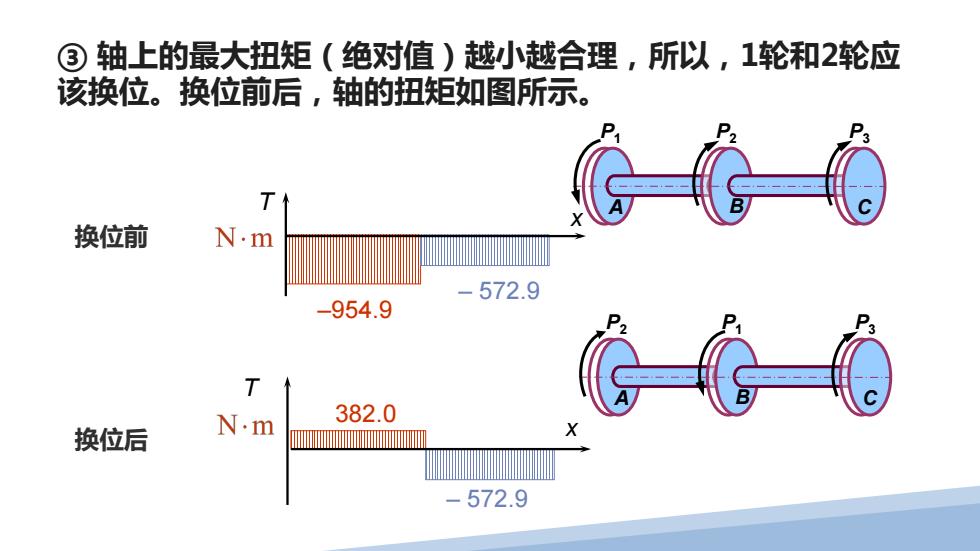
③轴上的最大扭矩(绝对值)越小越合理,所以,1轮和2轮应 该换位。换位前后,轴的扭矩如图所示。 T 换位前 N.m -572.9 -954.9 T 382.0 换位后 N.m -572.9
T 382.0 换位后 T x –954.9 – 572.9 换位前 P2 P1 P3 A B C P1 P2 P3 A B C ③ 轴上的最大扭矩(绝对值)越小越合理,所以,1轮和2轮应 该换位。换位前后,轴的扭矩如图所示。 – 572.9 x