6.3轴向拉压杆截面上的应力 应力的概念 内力大小不能衡量某点的局部强弱 应力:由外力引起的内力集度(密集程度)。 >破坏”或“失效”往往从内力集度最大处开始 △F 了压强? (面)平均应力Pm △A 单位面积上的内力,Pa→MPa △F △F (点)应力 p=lim A40△A 正应力:与截面垂直的应力 剪应力切应力:与截面相切的应力
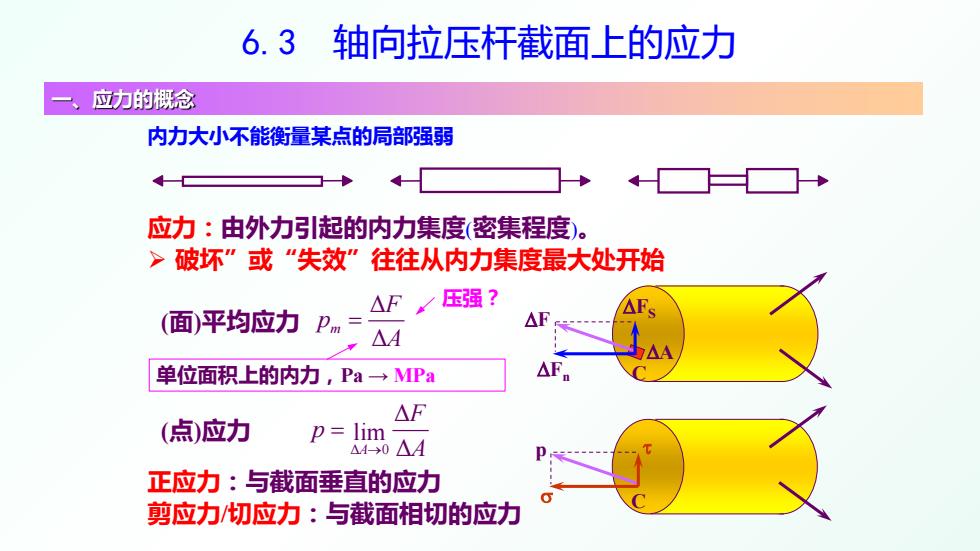
6.3 轴向拉压杆截面上的应力 一、应力的概念 ∆F ∆A C (面)平均应力 (点)应力 Δ Δ m F p A = Δ 0 Δ lim A Δ F p → A = 内力大小不能衡量某点的局部强弱 正应力:与截面垂直的应力 剪应力/切应力:与截面相切的应力 p C τ σ ∆Fn ∆FS 应力:由外力引起的内力集度(密集程度)。 破坏”或“失效”往往从内力集度最大处开始 单位面积上的内力,Pa → MPa 压强?

二 横截面上的应力 轴力并不能直接判断杆件强度,须用截面应力来度量。为了求应力分布,需先研究 杆件变形。 1.变形规律试验及平面假设: 横截面 变形前 受载后 变形前垂直轴线的直线,变形后仍为直线、仍垂直于轴线 平面假设:变形前为平面的横截面,变形后仍为平面、仍垂直于轴线。 >各纵向纤维变形相同
变形前 1.变形规律试验及平面假设: 平面假设:变形前为平面的横截面,变形后仍为平面、仍垂直于轴线。 各纵向纤维变形相同。 a c b d 受载后 a′ b′ F F d′ c ′ 变形前垂直轴线的直线,变形后仍为直线、仍垂直于轴线 轴力并不能直接判断杆件强度,须用截面应力来度量。为了求应力分布,需先研究 杆件变形。 二、横截面上的应力
2.拉伸应力: 各纵向纤维变形相等,力学性能相同(材料均匀),故受力相同,则横截面各点正应 力相等,即在横截面上均匀分布。 o F A >拉应力为正,压应力为负 例6-3图示阶梯轴横截面积A,=10cm2,A,=20cm2。求各段正应力。 解:画轴力图 左段应力:。=-100×10 Pa A 50kN 42 A10×10 100kN 150kN =100×10°Pa =100 MPa 右段应力:。=2=150x10 150kN A,20×10 =75×106Pa =75 MPa
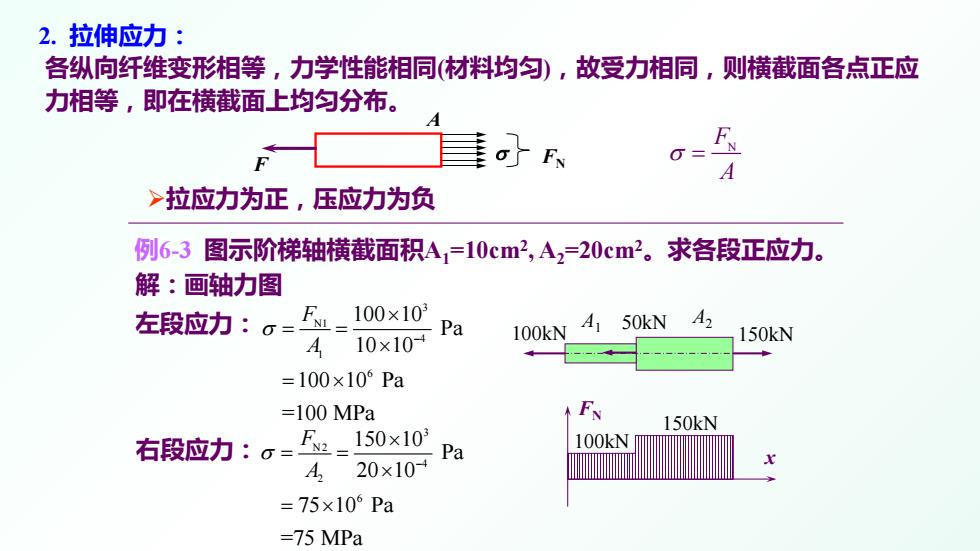
拉应力为正,压应力为负 2. 拉伸应力: 各纵向纤维变形相等,力学性能相同(材料均匀),故受力相同,则横截面各点正应 力相等,即在横截面上均匀分布。 F σ FN A FN A σ = 例6-3 图示阶梯轴横截面积A1=10cm2, A2=20cm2。求各段正应力。 150kN 100kN FN x 100kN 50kN 150kN A1 A2 解:画轴力图 左段应力: 右段应力: 3 N1 4 1 6 100 10 Pa 10 10 100 10 Pa =100 MPa σ − × = = × = × F A 3 N2 4 2 6 150 10 Pa 20 10 75 10 Pa =75 MPa σ − × = = × = × F A
斜截面上的应力 拉压破坏并不是总沿横截面发生,有时沿斜截面发生 平衡方程:F。F 几何关系:A=AC0sa cosa=o cosa A A a=Pa cosa=o cos2a =Pa sina=cosina cosa=osin2a 2 当a=0时,0zms=0o (横截面正应力最大) 当a=45时,z.l=受 (45°斜截面剪应力最大) 当a=90时,a=ta=0 (纵向截面无应力)
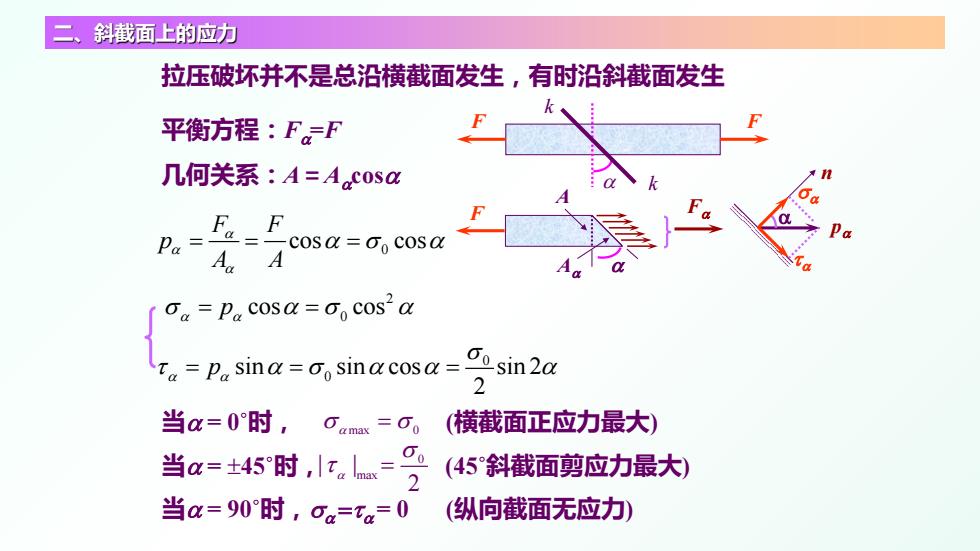
F F α k k 平衡方程:Fα =F 几何关系:A=Aαcosα 0 cos cos F F p A A α α α = = = ασ α 拉压破坏并不是总沿横截面发生,有时沿斜截面发生 当α = 90˚时,σα =τα= 0 (纵向截面无应力) α F Fα A Aα α pα n τα σα 当α = 0˚时, σ σ α max 0 = (横截面正应力最大) 当α = ±45˚时, (45˚斜截面剪应力最大) 0 max | | 2 α σ τ = 2 0 p cos cos σ ασ α α α = = 0 0 sin sin cos sin 2 2 p α α σ τ ασ α α α = = = 二、斜截面上的应力