
4. 5物体系的平衡 物体系:由若干个物体通过约束所组成的系统。 当整个系统平衡时,系统内每个物体都平衡;反之亦然。 >n个物体最多3n个方程(汇交、平行力系独立方程数会减少) 静定问题:系统未知量的数目不超过独立静力学平衡方程数目,可由平衡方程求出 全部未知量。 静不定问题或超静定问题:未知量的数目多于独立平衡方程数目,由静力学平衡方 程不能求出全部未知量。 >可能部分能求出,也可能全部求不出。 >需补充其它条件,如变形协调条件。 对物体系,可对每个物体列平衡方程,联立求解所有未知量。 但常关心部分量,这时可对少量对象列方程。 >整体+局部 常先整体分析求出一些约束。未知量尽量逐步求出,避免 >局部+整体 全体联立求解。 >局部+局部
4.5 物体系的平衡 静定问题:系统未知量的数目不超过独立静力学平衡方程数目,可由平衡方程求出 全部未知量。 静不定问题或超静定问题:未知量的数目多于独立平衡方程数目,由静力学平衡方 程不能求出全部未知量。 可能部分能求出,也可能全部求不出。 需补充其它条件,如变形协调条件。 物体系:由若干个物体通过约束所组成的系统。 当整个系统平衡时,系统内每个物体都平衡;反之亦然。 n个物体最多3n个方程(汇交、平行力系独立方程数会减少) 对物体系,可对每个物体列平衡方程,联立求解所有未知量。 但常关心部分量,这时可对少量对象列方程。 整体+局部 局部+整体 局部+局部 常先整体分析求出一些约束。未知量尽量逐步求出,避免 全体联立求解
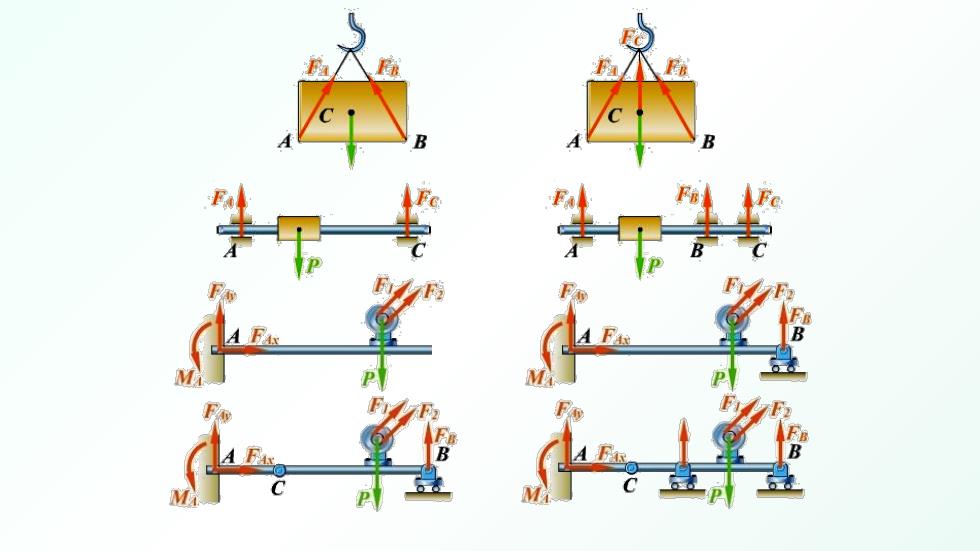

例4.5a已知:OA=R,AB=I,F,不计物体自重与摩擦, OA在水平位置平衡。 求:力偶矩M的大小,轴承O处的约束力,连杆AB受力, 冲头给导轨的侧压力。 解:(1)取冲头B,画受力图。 ΣFn=0F-Fcos0=0FB= F Fl os0√P-R2 FR Fis=0 Fy-Fg sin=0 .Fy =Ftan= V2-R2 (2)取轮,画受力图。 FR ΣFx=0Fox+F4sinb=0 V7-R2 ΣFn=0Fm+F4cos0=0∴.Fm=-F ∑M。=0 F cos0.R-M=0.M=FR
例4.5a 已知:OA=R,AB= l,F,不计物体自重与摩擦, OA在水平位置平衡。 求:力偶矩M 的大小,轴承O处的约束力,连杆AB受力, 冲头给导轨的侧压力。 解:(1)取冲头B,画受力图。 0 ∑ Fiy = cos 0 F F− = B θ 2 2 cos B F Fl F θ l R ∴= = − 0 ∑ Fix = sin 0 F F N B − = θ 2 2 tan N FR F F l R ∴= = θ − (2)取轮,画受力图。 0 ∑ Fix = sin 0 F F ox A + = θ 2 2 ox FR F l R ∴ =− − 0 ∑ Fiy = cos 0 F F oy A + = θ ∴ =− F F oy 0 ∑ M o = cos 0 F RM A θ ⋅− = ∴ = M FR F FA FOx FOy FB F FN θ

例4.5b已知:F=20kN,F10kN/m,M=20kNm,=1m。求:A、B处的约束力。 解:()取CD梁,画受力图。 2M。=0 Fasin601-gl-号-Fcos30°.21=0 60D .Fa=45.77kN (2)取整体,画受力图。 ∑F=0FAx-Fa cos60°-Fsin30°=0 .FAx=32.89N ∑F=0Fy+Fg sin60°-2ql-Fcos30°=0 .F=-2.32kN ∑M4=0 M4-M-2gl.2l+Fsin60°.3l-Fcos30°.4l=0 ∴.M4=10.37kN
例4.5b 已知: F=20kN,q=10kN/m,M=20kN·m,l=1m。求:A、B处的约束力。 解:(1)取CD梁,画受力图。 0 ∑ M c = sin 60 cos30 2 0 2 B l F l ql F l ⋅− ⋅ − ⋅ = ∴ = FB 45.77kN (2)取整体,画受力图。 0 ∑ Fix = cos 60 sin 30 0 FF F Ax B − −= ∴ = FAx 32.89kN 0 ∑ Fiy = sin 60 2 cos30 0 F F ql F Ay B + −− = ∴ =− FAy 2.32kN 0 ∑ M A = 2 2 sin 60 3 cos30 4 0 M M ql l F l F l A B − − ⋅+ ⋅− ⋅ = ∴ = M A 10.37kN
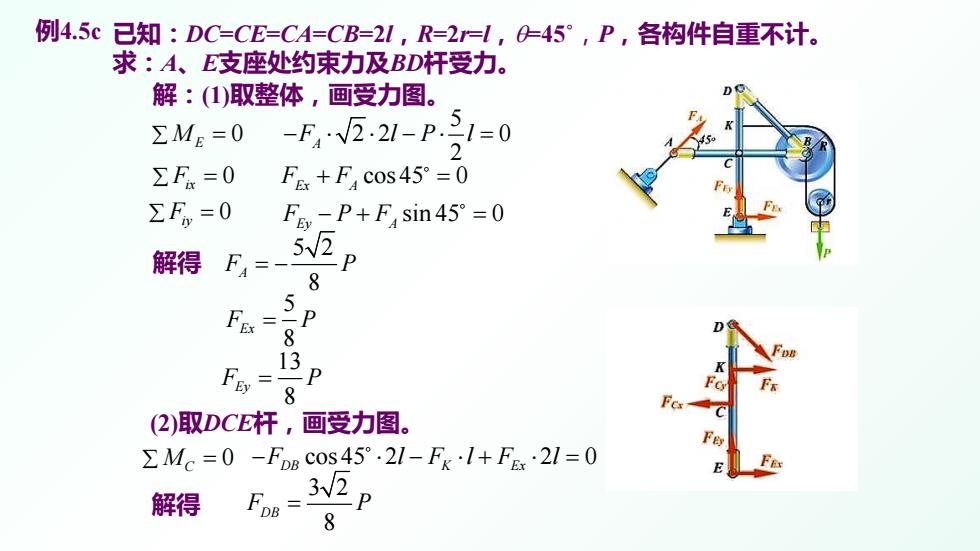
例4.5c已知:DC=CE=CA=CB=21,R=2=l,G45°,P,各构件自重不计。 求:A、E支座处约束力及BD杆受力。 解:(1)取整体,画受力图。 ∑ME=0 -FV221-P.1=0 ∑Fa=0F+Fcos45°=0 ∑F=0 F=P+F4sin45°=0 解得 F=- v _P 8 5 F=P 8 13 F6=。P 8 (2)取DCE杆,画受力图。 ΣMc=0-FpB COS45°.21-Fx·1+Fa·2l=0 E 解得 3W2 8
已知:DC=CE=CA=CB=2l,R=2r=l,θ=45˚ ,P,各构件自重不计。 求:A、E支座处约束力及BD杆受力。 例4.5c 解:(1)取整体,画受力图。 0 ∑ ME = 5 22 0 2 − ⋅ ⋅ −⋅ = F lP l A 5 2 8 解得 F P A = − 0 ∑ Fix = cos 45 0 F F Ex A + = 5 8 F P Ex = sin 45 0 F PF Ey −+ = A 0 ∑ Fiy = 13 8 F P Ey = (2)取DCE杆,画受力图。 解得 0 ∑ MC = cos 45 2 2 0 − ⋅ − ⋅+ ⋅ = F lFlF l DB K Ex 3 2 8 F P DB =

小结 对物体系,求部分未知量可有三种策略 >整体+局部 局部+整体 >局部+局部 (①)先分析谁,是希望能先求出一些量, 便于后续求解。理想的做法是未知量能逐步 求出,而不是最后全部方程联立求解。 (2)“局部”可以是系统的某个组成构件;还可以是某几个构件组成的局部结构。 (3)有时某个部分要分析2次:它涉及的未知量较多,首次时只能求出部分量;当其 它部分分析后(获得新的信息),再分析该部分求出其它量
(1)先分析谁,是希望能先求出一些量,便于后续求解。理想的做法是未知量能逐步 求出,而不是最后全部方程联立求解。 (2)“局部”可以是系统的某个组成构件;还可以是某几个构件组成的局部结构。 (3)有时某个部分要分析2次:它涉及的未知量较多,首次时只能求出部分量;当其 它部分分析后(获得新的信息),再分析该部分求出其它量。 对物体系,求部分未知量可有三种策略 整体+局部 局部+整体 局部+局部 小结