
目录 CONTENTS 么1 外力偶矩的计算 2 扭矩的计算 3 扭矩图的绘制
123 外力偶矩的计算 扭矩的计算 扭矩图的绘制 目录 CONTENTS
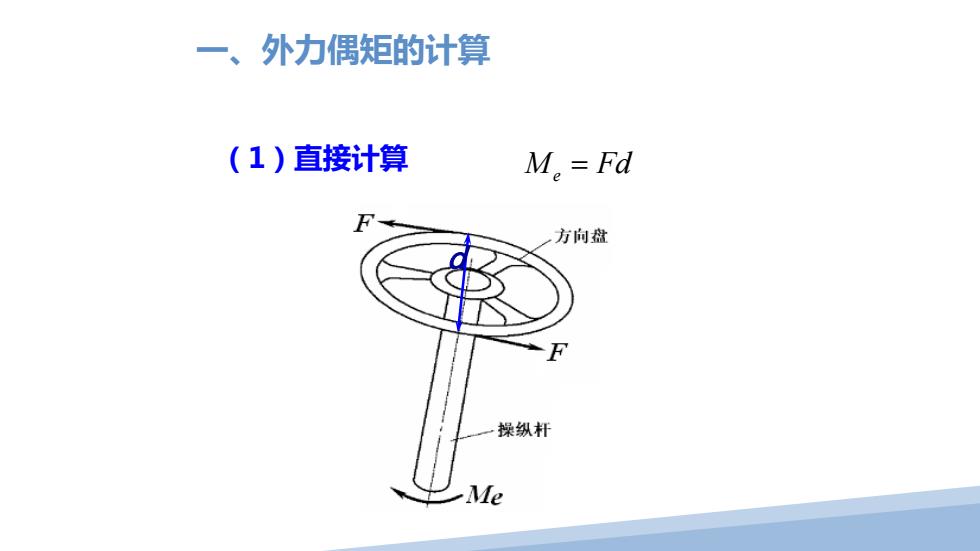
一、外力偶矩的计算 (1)直接计算 M。=Fd 方向盘 操纵杆 Me
(1)直接计算 d M Fd e = 一、外力偶矩的计算
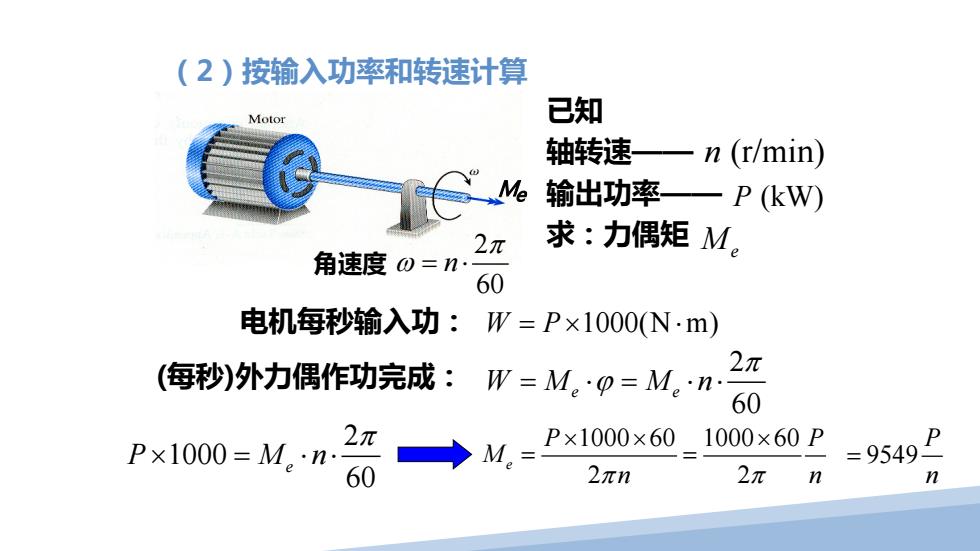
(2)按输入功率和转速计算 Motor 已知 轴转速一一n(r/min) Me 输出功率—一P(kW 2π 求:力偶矩M。 角速度0=n: 60 电机每秒输入功:W=P×1000(Nm) (每秒)外力偶作功完成:W=M。·p=M。n: 2π 60 2元 P×1000=M。·n: M,= P×1000×601000×60P P =9549 60 2πn 2π n n
(2)按输入功率和转速计算 电机每秒输入功: (每秒)外力偶作功完成: 2 60 W M Mn e e π = ⋅ = ⋅⋅ ϕ 已知 轴转速—— 输出功率—— 求:力偶矩 n (r/min) P (kW) M e 2 1000 60 P Mn e π × = ⋅⋅ 9549 P n = Me 1000 60 1000 60 2 2 e P P M π π n n ×× × = = W P =× ⋅ 1000(N m) 角速度 2 60 n π ω = ⋅
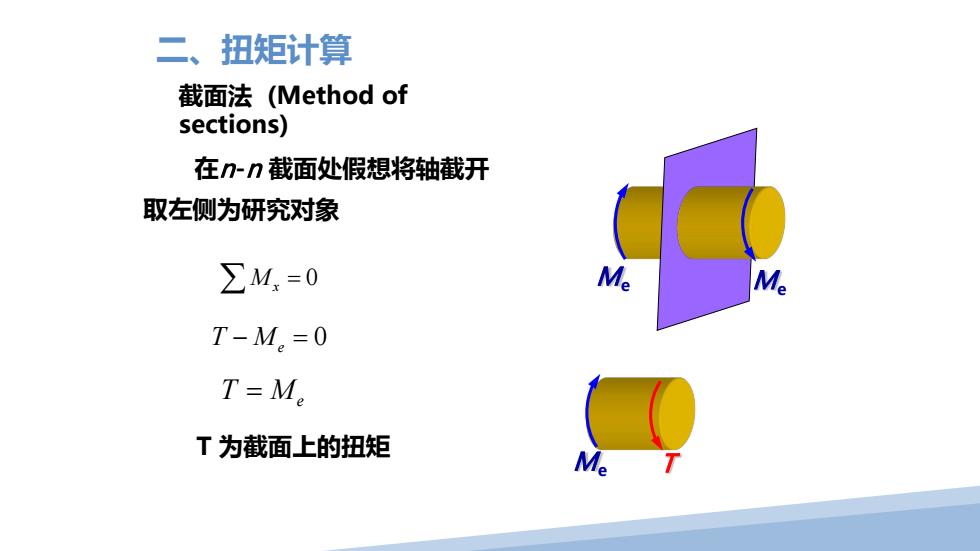
二、 扭矩计算 截面法(Method of sections) 在n-n截面处假想将轴截开 取左侧为研究对象 ∑M=0 Me Me T-M。=0 T=M。 T为截面上的扭矩
Me 在n-n 截面处假想将轴截开 取左侧为研究对象 截面法 (Method of sections) T 0 ∑ M x = Me Me 二、扭矩计算 0 T M− = e T M= e T 为截面上的扭矩

二、扭矩计算 扭矩正负规定 Me Me 右手螺旋法则:右手四指内屈,与扭矩转向相同,则拇指的指 向表示扭矩矢的方向,若扭矩矢方向与截面外法线相同,规定扭 矩为正,反之为负。 右手拇指指向截面的外法线方向为正(+),反之为负(-)
扭矩正负规定 右手螺旋法则:右手四指内屈,与扭矩转向相同,则拇指的指 向表示扭矩矢的方向,若扭矩矢方向与截面外法线相同,规定扭 矩为正,反之为负。 右手拇指指向截面的外法线方向为正(+),反之为负(-) 二、扭矩计算 Me x • Me • x T

三、扭矩图 扭矩图:表示沿杆件轴线各横截面上扭矩变化规律的图线。 T ⊕ 用平行于杆轴线的坐标×表示横截面的位置;用垂直于杆轴线 的坐标T表示横截面上的扭矩,正的扭矩画在×轴上方,负的扭矩 画在x轴下方。 目的: ①扭矩变化规律; ②1max值及其截面位置→ 强度计算(危险截面)
扭矩图:表示沿杆件轴线各横截面上扭矩变化规律的图线。 目的: ①扭矩变化规律; ②|T|max值及其截面位置 强度计算(危险截面) 三、扭矩图 用平行于杆轴线的坐标 x 表示横截面的位置;用垂直于杆轴线 的坐标 T 表示横截面上的扭矩,正的扭矩画在 x 轴上方,负的扭矩 画在 x 轴下方

例:如图,主动轮A的输入功率PA=36kW,从动轮B、C、D输出 功率分别为PB=PC=11kW,PD=14kW,轴的转速n=300r/min。 试画出传动轴的扭矩图。 L M M 36 M4=9549× =1146N.m 300 M=Mc=350N.m M,=446Nm T+Ma=0 T=-M =-350N.m Mg+Mc+T=0 T =-700N.m T-Mp=0 T,=446N·m 446 TN.m) ⊕ 最大扭矩发生在CA段,CA段为危险截面。 注意:图名、单位、对齐、正负号、扭矩值 350 ⊕ 700
例:如图,主动轮A的输入功率PA = 36kW,从动轮B、C、D输出 功率分别为PB = PC = 11kW,PD = 14kW,轴的转速n=300r/min。 试画出传动轴的扭矩图。 最大扭矩发生在 CA 段, CA 段为危险截面。 注意:图名、单位、对齐、正负号、扭矩值 M MA B MC B C A D 1 MD 1 2 2 3 3
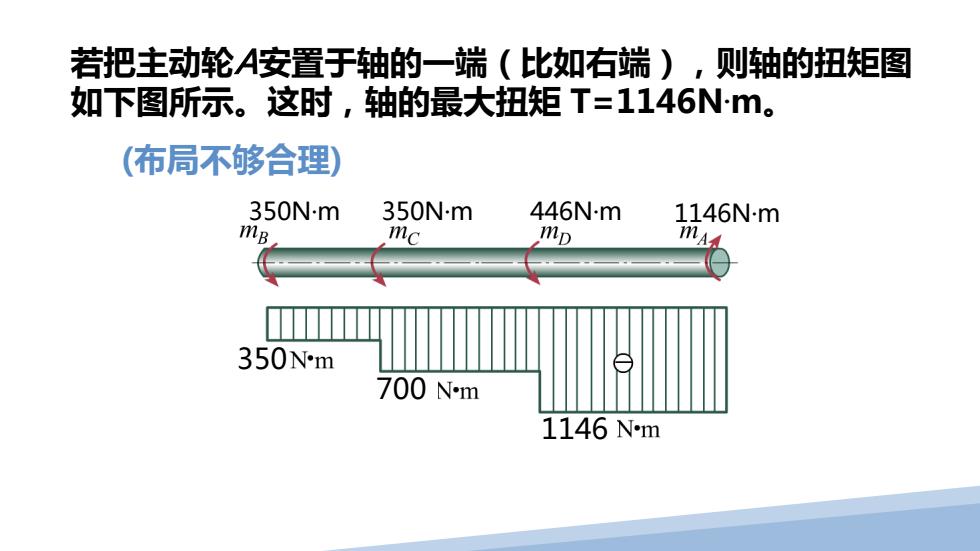
若把主动轮A安置于轴的一端(比如右端),则轴的扭矩图 如下图所示。这时,轴的最大扭矩T=1146Nm。 (布局不够合理) 350Nm 350Nm 446Nm 1146Nm mB mc mD mA 350Nm 700Nm 1146Nm
若把主动轮A安置于轴的一端(比如右端),则轴的扭矩图 如下图所示。这时,轴的最大扭矩 T=1146N. m。 (布局不够合理) 350 700 1146 350N·m 350N·m 446N·m 1146N·m