
目录 CONTENTS 1 两端铰支细长压杆的临界压力推导 人2 讨论分析 人3 矩形截面的细长压杆的失稳
1 2 3 两端铰支细长压杆的临界压力推导 讨论分析 矩形截面的细长压杆的失稳 目录 CONTENTS

1.两端较支细长压杆的临界压力推导 如图:两端铰支杆受压力F作用 假设:压杆在微弯平衡状态,即压杆处于 平衡稳定和不稳定平衡之间的临界状态。 研究微弯平衡状态 处截面的弯矩 ∑M=0M+Fw=0 M=-Fw
1. 两端铰支细长压杆的临界压力推导 m x m w O x y l F m m F M( x)= -Fw x y O w 如图:两端铰支杆受压力F作用 假设:压杆在微弯平衡状态,即压杆处于 平衡稳定和不稳定平衡之间的临界状态。 x处截面的弯矩 M Fw = − ∑ M M Fw = += 0 0 研究微弯平衡状态

1.推导两端铰支细长压杆的临界压力 己知:M=-Fw 代入挠曲线近似微分方程 d2w d2w M +k2w=0 -Fw dx2 dx2 EI EI 通解:w=Asin kx+Bcos kx d2w 即 A、B为积分常数,待定 El 边界条件:(④x=0时,得 B=0 F w=0 w=Asin kx 记k2= EI
2 2 d d w M x EI = M Fw = − Fw EI − = 2 2 d d w F w x EI 即 = − 2 F k EI 记 = 2 2 2 d 0 d w k w x + = 通解: 代入挠曲线近似微分方程 w A kx B kx = + sin cos A、B为积分常数,待定 已知: M Fw = − 1. 推导两端铰支细长压杆的临界压力 边界条件: (1) x = 0 时, w = 0 得 0 sin B w A kx = = x O x y l F
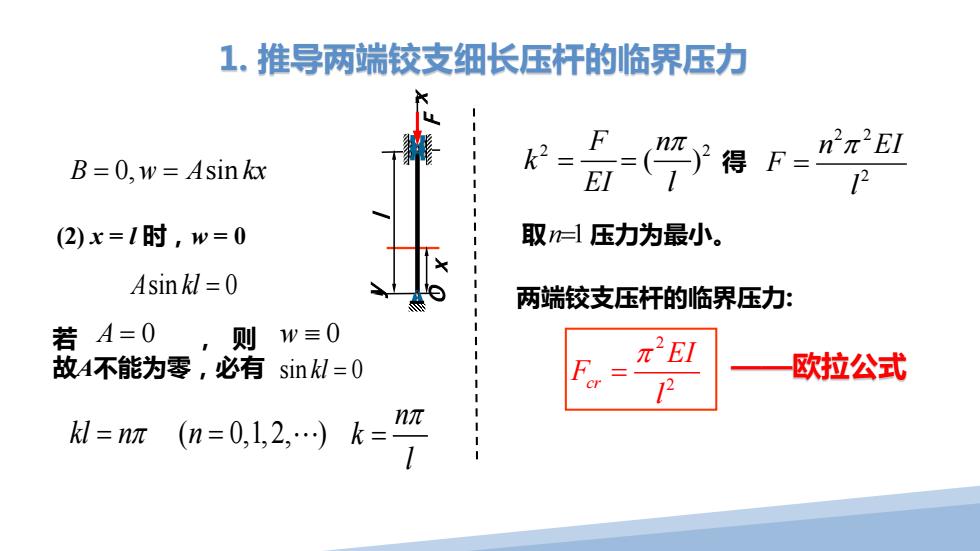
1.推导两端铰支细长压杆的临界压力 n2π2El B=0.w=Asin kx k2= EI 12 (2)x=1时,w=0 取=压力为最小。 Asin kl =0 两端铰支压杆的临界压力: 若A=0 则W三0 故A不能为零,必有sinl=0 π2EI 欧拉公式 kl=nn (n=0,12,k= 1
A kl sin 0 = kl n n = = π ( 0,1,2, ) n k l π = (2) x = l 时,w = 0 2 F k EI = 2 ( ) n l π = 得 2 2 2 n EI F l π = 若 , 则 故A不能为零,必有 A = 0 w ≡ 0 sin 0 kl = 取 压力为最小。 2 cr 2 EI F l π = ——欧拉公式 两端铰支压杆的临界压力: 1. 推导两端铰支细长压杆的临界压力 x O x y l F B w A kx = = 0, sin

2.讨论分析 π2E1 1)两端铰支压杆的临界压力 )弯曲曲线公式w=Asn?x,半个正弦波曲线 3)几点说明: >只适用于线弹性下两端铰支的理想压杆。 >A数值不能确定。 >I-各个方向约束情况相同时,应该取最小的形心主惯性矩
2. 讨论分析 2 cr 2 EI F l π 两端铰支压杆的临界压力 = wA x sin l π = 只适用于线弹性下两端铰支的理想压杆。 A数值不能确定。 I-各个方向约束情况相同时,应该取最小的形心主惯性矩。 1) 2)弯曲曲线公式 ,半个正弦波曲线。 3)几点说明:

3.矩形截面的细长压杆失稳 举例:矩形截面在哪个平面内失稳?(绕哪个轴转动) .h>b 12>IyF= π2Ely 12 所以矩形截面压杆首先在xz平面内失稳弯曲(即绕y轴转动)
z y b h 举例:矩形截面在哪个平面内失稳?(绕哪个轴转动) x y z h b F F 3 y h 12 1 I = b 3 z bh 12 1 I = h b y I I ∴ Z 所以矩形截面压杆首先在xz平面内失稳弯曲(即绕 y 轴转动). 3 . 矩形截面的细长压杆失稳