
南阳师院课程(课时)教学计划 课 程:材料力学 教 师: 叶铁 院(系):机械电子工程学院 学年学期:2017年第一学期
南阳师院课程(课时)教学计划 课 程: 材 料 力 学 教 师: 叶铁 院(系): 机械电子工程学院 学年学期: 2017 年第一学期

南阳师范学院课程教学安排 教材名称及使用版本 材料力学刘鸿文,高等教有出版礼 本课程教学计划课时数 54 本课程实际安排课时数 位 第一章:绪论4学时 第二章拉伸、压缩与剪切12学时 教学 第三章扭转8学时 内 第四章弯曲内力8学时 第五章弯曲应力8学时 时 分 第六章弯曲变形. ……8学时 第七章应力和应变分析、强度理论8学时 第八章组合变形 …8学时 第九章压杆稳定 .8学时 备
南阳师范学院课程教学安排 教材名称及使用版本 材料力学 刘鸿文,高等教育出版社 本课程教学计划课时数 54 本课程实际安排课时数 72 教 学 内 容 及 课 时 分 配 情 况 第一章:绪论………………………………………………4 学时 第二章 拉伸、压缩与剪切………………………………12 学时 第三章 扭 转………………………………………………8 学时 第四章 弯曲内力…………………………………………8 学时 第五章 弯曲应力……….…………...……………………8 学时 第六章 弯曲变形…………………………………………8 学时 第七章 应力和应变分析、强度理论……………………8 学时 第八章 组合变形…………………………………………8 学时 第九章 压杆稳定…………………………………………8 学时 备 注

南阳师范学院课时教学计划 章节 第一章 课题 绪论 计划课时数2 授课班级 机械电子15 教 学 的 教 学 材料力学的任务,变形固体性质的基本假设 教 学 内力、截面法及应力的概念 难 点 学 课堂讲授 方 幻灯演示 法 和 课后作业 手 课堂讨论 段 注
南阳师范学院课时教学计划 章节 第一章 课题 绪论 计划课时数 2 授课班级 机械电子 15 教 学 目 的 教 学 重 点 材料力学的任务,变形固体性质的基本假设 教 学 难 点 内力、截面法及应力的概念 教 学 方 法 和 手 段 课堂讲授 幻灯演示 课后作业 课堂讨论 备 注

教学内容 批注 第一章:绪论 1.1材料力学的任务 起骨架作用的部分,称为结构。 组成结构或机械的单个部分则称为构件或零件。如:桥梁的桥墩、 桥面等。 每一构件都应满足一定的条件,这些条件主要是指经济与安全。 所谓经济是指构件应采用适当的材料并使截面尺寸最小(消耗最少的 材料):安全则是指构件在受力或受外界因素(如温度改变、地基沉陷 等)影响时,应同时满足强度、刚度及稳定性三方面的要求。即:安 全包括三个 足够的强度 一构件具有足够的抵抗破坏的能力: 把变形控制在 的范围 一构件具有足够的抵抗变形的能力,即要 (3)足够的稳 定性 —构件具有足够的保持原有平衡形式的 能力 构件在强度、刚度和稳定性三方面所具有的能力统称为构件的承 载能 经济与安全是一对矛盾的两个方面。而材料力学就是要解决这 矛盾,即是研究构件在各种外力或外界因素影响下的强度、刚度和稳 定性的原理及计算方法的科学。包括对材料的力学性质的研究。这就 是材料力学的任务。 1.2材料力学与生产实践的关系 生美提学的发展:材料力学的发展又反过未对 1.3可变形固体的性质及其基本假设 任何固体在外力作用下都要产生形状及尺寸的改变 -即变形。 外力大到一定程度构件还会发生破坏,这种固体称为“变形固体”。承 认构件的变形,是材料力学研究问题、解决问题的基本前提。 变形包括:(1)弹性变开 变形 外力去掉后可消失的变 一外力去掉后不能消失的变形。 关于变形固 的 本假设 毫无空隙 连续性假设:材料内部连续、密实地充满着物质而 均匀性假设:材料沿各部分的力学性能完全相同: 全相同。 这样的材料称为各向同性材料,否则称头 各向异性材 4.小变形假设:认为受力后构件的变形与其本身尺寸相比很小 小变形包括两方面含义:(1)变形与原始尺寸在量级上进行比较 很小:(2)变形对外力的影响很小 一不会显著改变外力的作用位置 或不产生新的外力成分。 1.4材料力学主要研究对象(杆件)的几何特征
教 学 内 容 批注 第一章:绪论 1.1 材料力学的任务 建筑物承受荷载而起骨架作用的部分,称为结构。 组成结构或机械的单个部分则称为构件或零件。如:桥梁的桥墩、 桥面等。 每一构件都应满足一定的条件,这些条件主要是指经济与安全。 所谓经济是指构件应采用适当的材料并使截面尺寸最小(消耗最少的 材料);安全则是指构件在受力或受外界因素(如温度改变、地基沉陷 等)影响时,应同时满足强度、刚度及稳定性三方面的要求。即:安 全包括三个方面: (1)足够的强度──构件具有足够的抵抗破坏的能力; (2)足够的刚度──构件具有足够的抵抗变形的能力,即要 把变形控制在一定的范围内; (3)足够的稳定性──构件具有足够的保持原有平衡形式的 能力。 构件在强度、刚度和稳定性三方面所具有的能力统称为构件的承 载能力。 经济与安全是一对矛盾的两个方面。而材料力学就是要解决这一 矛盾,即是研究构件在各种外力或外界因素影响下的强度、刚度和稳 定性的原理及计算方法的科学。包括对材料的力学性质的研究。这就 是材料力学的任务。 1.2 材料力学与生产实践的关系 生产的发展推动了材料力学的发展;材料力学的发展又反过来对 生产实践起着重要的指导作用。 1.3 可变形固体的性质及其基本假设 任何固体在外力作用下都要产生形状及尺寸的改变──即变形。 外力大到一定程度构件还会发生破坏,这种固体称为“变形固体”。承 认构件的变形,是材料力学研究问题、解决问题的基本前提。 变形包括:(1)弹性变形──外力去掉后可消失的变形; (2)塑性变形──外力去掉后不能消失的变形。 关于变形固体性质的基本假设: 1. 连续性假设:材料内部连续、密实地充满着物质而 毫无空隙; 2. 均匀性假设:材料沿各部分的力学性能完全相同; 3.各向同性假设:材料沿各方向的力学性能完全相同。 这样的材料称为各向同性材料,否则称为各向异性材料。 4.小变形假设:认为受力后构件的变形与其本身尺寸相比很小。 小变形包括两方面含义:(1)变形与原始尺寸在量级上进行比较, 很小;(2)变形对外力的影响很小──不会显著改变外力的作用位置 或不产生新的外力成分。 1.4 材料力学主要研究对象(杆件)的几何特征

所谓杆,是指其纵向(沿长度方向)尺寸比其横向(垂直于长度 方向)尺寸 多的构件。我们常见的柱、梁和传动轴等均属于杆。 杆件的两个九贺发素:垂直于杆件长度方向的藏面称为杆的横截 面。 轴线:各横截面形心的连线称为杆的轴线 直杆的轴线为直线: 的轴线为曲线。 横截 马杆轴不恋老 为等截面杆: 改变者称为变截面杆。杆轴线为直线,横截面沿杆轴又 不变者称为等截面直杆,简称等直杆。 1.5杆件变形的基本形式 作用在构件上的荷载是各种各样的,因此,杆件的变形形式就呈 现出多样性,并且有时比较复杂。但分解来看,变形的基本形式却 有四种。 称为轴向拉伸或轴向压缩 其受力特性为外力的作用线与杆件的 轴线重合。变形特征为杆件沿轴线方向伸长或缩短。 2.前切 在一对相距很近的大小相等、方向相反、作用线与 杆轴线垂直的外力作用下,杆的主要变形是横截面沿外力作用方向发 生错动。这种变形形式称为剪切。其受力特性为一对大小相等、方向 相反的外力的作用线与杆轴线垂直且相距很近。变形特征为横截面沿 外力作用方向发生相对错动, ):扭转在一对大小相等、转向相反,作用面与杆轴线垂直 的外力偶作用下,杆件的任意两横截面米 变形特征为: 截面等 杆轴线发 作用平面与杆轴线垂直。 弯 相反的外力 这时杆将在纵向平 面 面发生相头 这种恋形形 为弯曲 生性为 卫面在 杆轴线在内的纵向平面内。变形特征为杆件的轴线由直线变为曲线, 任意两横截面发生相对倾斜。 工程中常用构件在荷载作用下的变形,在很多情况下都包含有两 种或两种以上的基本变形,我们把这种变形形式称为组合变形
所谓杆,是指其纵向(沿长度方向)尺寸比其横向(垂直于长度 方向)尺寸 大得多的构件。我们常见的柱、梁和传动轴等均属于杆。 杆件的两个几何元素: 1. 横截面:垂直于杆件长度方向的截面称为杆的横截 面。 2. 轴线:各横截面形心的连线称为杆的轴线。 直杆的轴线为直线;曲杆的轴线为曲线。横截面沿杆轴不变者称 为等截面杆;改变者称为变截面杆。杆轴线为直线,横截面沿杆轴又 不变者称为等截面直杆,简称等直杆。 1.5 杆件变形的基本形式 作用在构件上的荷载是各种各样的,因此,杆件的变形形式就呈 现出多样性,并且有时比较复杂。但分解来看,变形的基本形式却只 有四种。 1.轴向拉伸或轴向压缩 在一对大小相等、方向相反、作用线 与杆轴线重合的外力作用下,杆件将发生伸长或缩短变形,这种变形 形式称为轴向拉伸或轴向压缩。其受力特性为外力的作用线与杆件的 轴线重合。变形特征为杆件沿轴线方向伸长或缩短。 2.剪切 在一对相距很近的大小相等、方向相反、作用线与 杆轴线垂直的外力作用下,杆的主要变形是横截面沿外力作用方向发 生错动。这种变形形式称为剪切。其受力特性为一对大小相等、方向 相反的外力的作用线与杆轴线垂直且相距很近。变形特征为横截面沿 外力作用方向发生相对错动。 3.扭转 在一对大小相等、转向相反、作用面与杆轴线垂直 的外力偶作用下,杆件的任意两横截面将绕轴线发生相对转动,这种 变形形式称为扭转。其受力特性为外力偶的作用平面与杆轴线垂直。 变形特征为任意两相邻横截面绕杆轴线发生相对转动。 4.弯曲 在杆的一个纵向平面内,作用一对大小相等、转向 相反的外力偶,这时杆将在纵向平面内弯曲,任意两横截面发生相对 倾斜,这种变形形式称为弯曲。其受力特性为外力偶的作用平面在含 杆轴线在内的纵向平面内。变形特征为杆件的轴线由直线变为曲线, 任意两横截面发生相对倾斜。 工程中常用构件在荷载作用下的变形,在很多情况下都包含有两 种或两种以上的基本变形,我们把这种变形形式称为组合变形

南阳师范学院课时教学计划 章节 第二章 课题 拉伸、压缩与剪切 计划课时数6 授课班级 机械电子15 学 目 的 教 1.讲清基本概念 学 2.理清分析问题的思路。 重 点 教 学 1.轴向拉伸或压缩时横截面上的内力和应力 2.直杆轴向拉伸或压缩时斜截面上的应力 按 3.材料拉伸时的力学性能 点 教 鸿 课堂讲授 方 法 幻灯演示 和 课后作业 手 课堂讨论 段 备 注
南阳师范学院课时教学计划 章节 第二章 课题 拉伸、压缩与剪切 计划课时数 6 授课班级 机械电子 15 教 学 目 的 教 学 重 点 1.讲清基本概念; 2. 理清分析问题的思路。 教 学 难 点 1.轴向拉伸或压缩时横截面上的内力和应力 2.直杆轴向拉伸或压缩时斜截面上的应力 3.材料拉伸时的力学性能 教 学 方 法 和 手 段 课堂讲授 幻灯演示 课后作业 课堂讨论 备 注
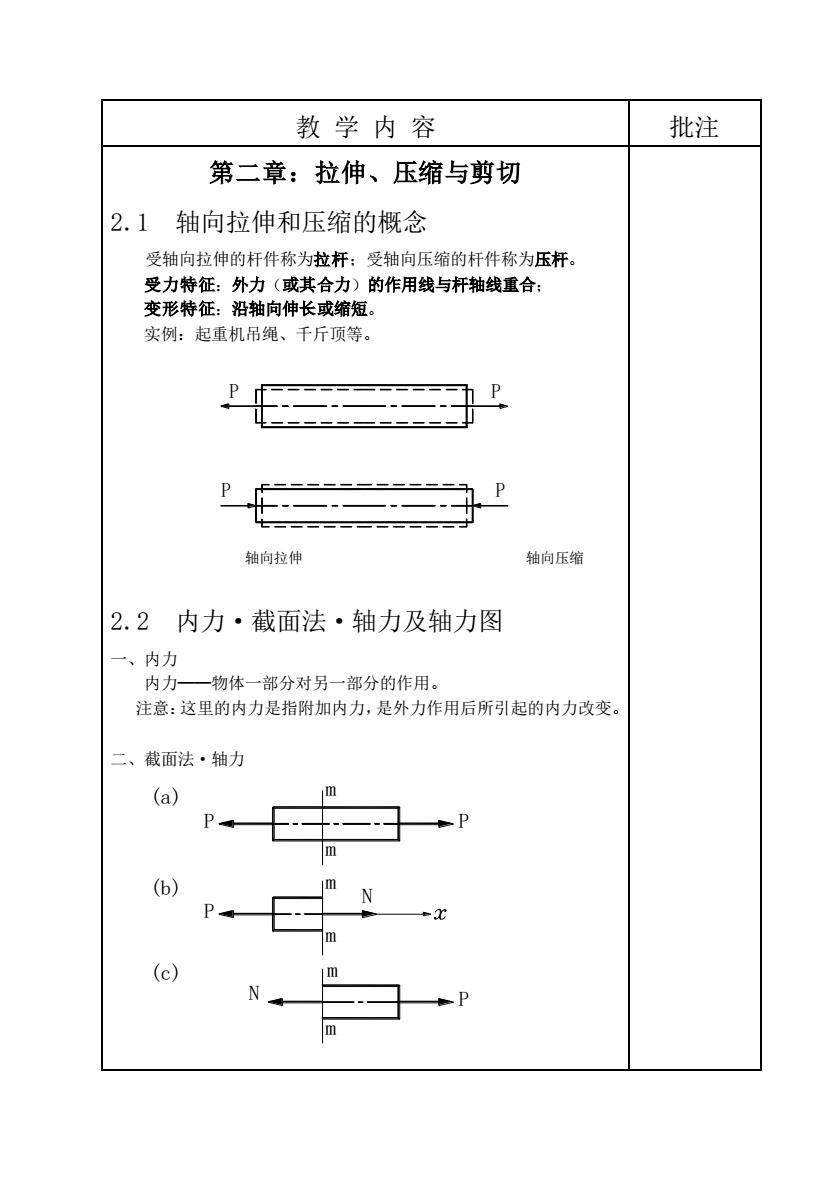
教学内容 批注 第二章:拉伸、压缩与剪切 2.1轴向拉伸和压缩的概念 受轴向拉伸的杆件称为拉杆:受轴向压缩的杆件称为压杆。 受力特征:外力(或其合力)的作用线与杆轴线重合: 变形特征:沿轴向伸长或缩短。 实例:起重机吊绳、千斤顶等。 ---hP P 轴向拉伸 轴向压缩 2.2内力·截面法·轴力及轴力图 、内力 内力—物体一部分对另一部分的作用。 注意:这里的内力是指附加内力,是外力作用后所引起的内力改变 、 截面法·轴力 (a) m P P m (b) m N m
教 学 内 容 批注 第二章:拉伸、压缩与剪切 2.1 轴向拉伸和压缩的概念 受轴向拉伸的杆件称为拉杆;受轴向压缩的杆件称为压杆。 受力特征:外力(或其合力)的作用线与杆轴线重合; 变形特征:沿轴向伸长或缩短。 实例:起重机吊绳、千斤顶等。 P P P P 轴向拉伸 轴向压缩 2.2 内力·截面法·轴力及轴力图 一、内力 内力──物体一部分对另一部分的作用。 注意:这里的内力是指附加内力,是外力作用后所引起的内力改变。 二、截面法·轴力 P P (a) P (b) P (c) N m m m m m m N

受外力作用而处于平衡的物体,其内力可用截面法显示并确定。 用裁面法求构件内力可归纳为以下三个步骤: 1.截开在需要求内力的截面处,假想地将杆截分为两部分: 2.代替取截开后的任一部分作为研究对象(称为隔离体),并 把弃去部分对保留部分的作用以截开面上的内力代替: 3.平衡对保留部分即隔离体建立平衡方程,计算内力的大小和 方向。 如图所示拉杆,由截面法可得mm截面上的内力 N=P 在此说明取左、右部分为研究对象,结果相同。 由于拉压杆横截面上的内力N的作用线与杆轴线重合,因此,拉 压杆的内力也称为轴力。 符号规定:拉杆的变形是轴向伸长,其轴力为正,称为拉力,方 向是背离截面的:压杆的变形是轴向缩短,其轴力为负,称为压力, 方向是指向截面的。 必须指出,在采用截面法之前,不能随意使用静力学中力(或力 偶)的可移性原理,以及力的等效代换。因为这样就会改变构件的变 形性质,并使内力也随之改变。但在截开后建立隔离体的平衡方程时, 则可以使用力的等效代换及可移性原理。 三、轴力图 为了表明轴力随横截面位置的变化情况,通常作出轴力图。其什 法如下:选取一定的比例尺,用平行于杆轴线的坐标表示横截面的位 置,用垂直于杆轴线的坐标表示横截面上轴力的数值,从而绘出表示 轴力与横截面位置关系的图形,称为轴力图。通常将正值的轴力画在 上侧,负值的画在下侧。 2.3横截面及斜截面上的应力 要解决强度问题,不仅要知道构件沿哪个截面破坏,而且要知道 从其上哪一点破坏。 应力一是受力构件某一截面分布内力在一点处的集度。 、 应力的概念 平均应力一P= .△p 一般地说,截面上的分布内力并不是均匀的,故平均应力pm的大 小和方向将随所取微面积△A的大小而不同。为表明分布内力在M点 处的集度,令△A一0,则得△P/△A的极限值P,即 卫称为M点处的总应力,其方向一般既不与截面垂直,也不与截面相
受外力作用而处于平衡的物体,其内力可用截面法显示并确定。 用截面法求构件内力可归纳为以下三个步骤: 1.截开 在需要求内力的截面处,假想地将杆截分为两部分; 2.代替 取截开后的任一部分作为研究对象(称为隔离体),并 把弃去部分对保留部分的作用以截开面上的内力代替; 3.平衡 对保留部分即隔离体建立平衡方程,计算内力的大小和 方向。 如图所示拉杆,由截面法可得 m-m 截面上的内力 N = P 在此说明取左、右部分为研究对象,结果相同。 由于拉压杆横截面上的内力 N 的作用线与杆轴线重合,因此,拉 压杆的内力也称为轴力。 符号规定:拉杆的变形是轴向伸长,其轴力为正,称为拉力,方 向是背离截面的;压杆的变形是轴向缩短,其轴力为负,称为压力, 方向是指向截面的。 必须指出,在采用截面法之前,不能随意使用静力学中力(或力 偶)的可移性原理,以及力的等效代换。因为这样就会改变构件的变 形性质,并使内力也随之改变。但在截开后建立隔离体的平衡方程时, 则可以使用力的等效代换及可移性原理。 三、轴力图 为了表明轴力随横截面位置的变化情况,通常作出轴力图。其作 法如下:选取一定的比例尺,用平行于杆轴线的坐标表示横截面的位 置,用垂直于杆轴线的坐标表示横截面上轴力的数值,从而绘出表示 轴力与横截面位置关系的图形,称为轴力图。通常将正值的轴力画在 上侧,负值的画在下侧。 2.3 横截面及斜截面上的应力 要解决强度问题,不仅要知道构件沿哪个截面破坏,而且要知道 从其上哪一点破坏。 应力──是受力构件某一截面分布内力在一点处的集度。 一、应力的概念 平均应力── A p pm = 一般地说,截面上的分布内力并不是均匀的,故平均应力 pm 的大 小和方向将随所取微面积ΔA 的大小而不同。为表明分布内力在 M 点 处的集度,令ΔA→0,则得ΔP/ΔA 的极限值 p,即 dA dP A p p A = = →0 lim p 称为 M 点处的总应力,其方向一般既不与截面垂直,也不与截面相
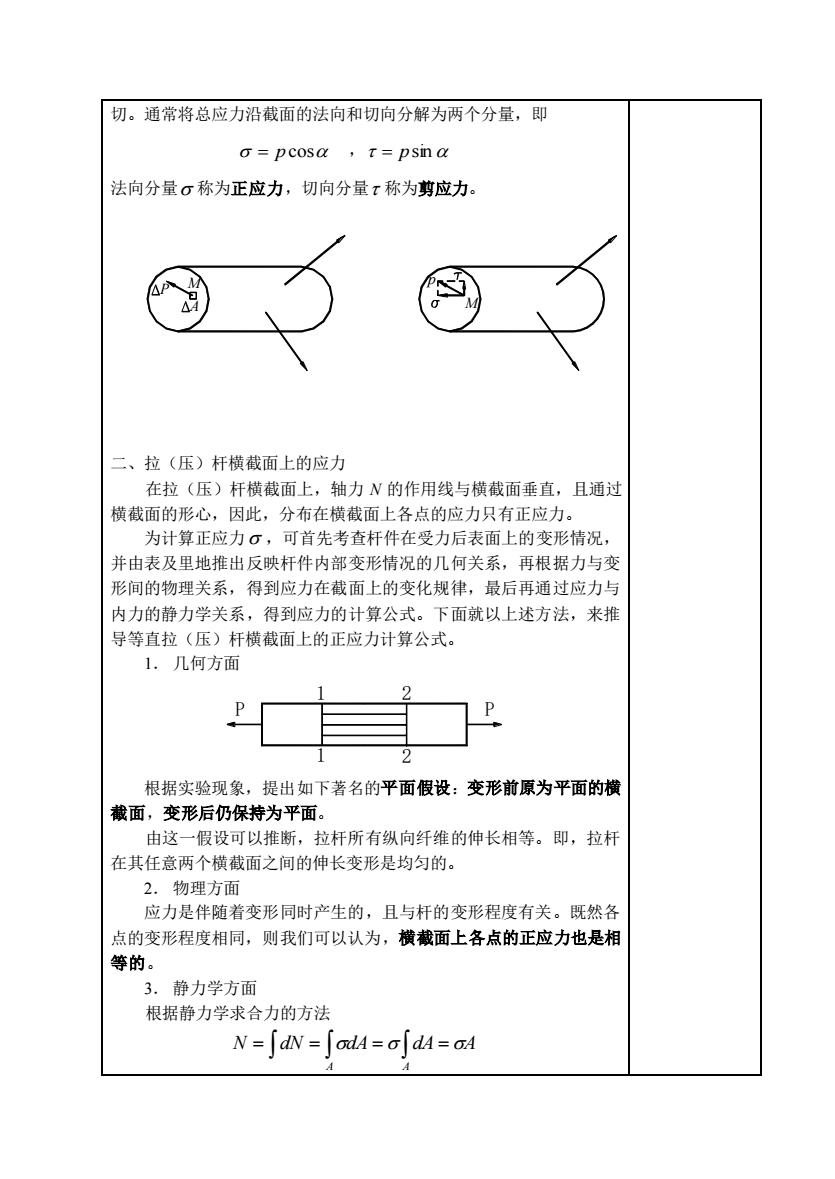
切。通常将总应力沿截面的法向和切向分解为两个分量,即 o=pcosa,r=psina 法向分量。称为正应力,切向分量x称为剪应力。 二、拉(压)杆横截面上的应力 在拉(压)杆横截面上,轴力N的作用线与横截面垂直,且通过 横截面的形心,因此,分布在横截面上各点的应力只有正应力。 为计算正应力。,可首先考查杆件在受力后表面上的变形情况, 并由表及里地推出反映杆件内部变形情况的几何关系,再根据力与变 形间的物理关系,得到应力在截面上的变化规律,最后再通过应力与 内力的静力学关系,得到应力的计算公式。下面就以上述方法,来推 导等直拉(压)杆横截面上的正应力计算公式。 1.几何方面 2 根据实验现象,提出如下著名的平面假设:变形前原为平面的横 截面,变形后仍保持为平面。 由这一假设可以推断,拉杆所有纵向纤维的伸长相等。即,拉 在其任意两个横截面之间的伸长变形是均匀的。 2.物理方面 应力是伴随着变形同时产生的,且与杆的变形程度有关。既然各 点的变形程度相同,则我们可以认为,横截面上各点的正应力也是相 等的。 3.静力学方面 根据静力学求合力的方法 N=「dN=「odA=o「dA=aA
切。通常将总应力沿截面的法向和切向分解为两个分量,即 = p cos , = psin 法向分量 称为正应力,切向分量 称为剪应力。 P M A M p 二、拉(压)杆横截面上的应力 在拉(压)杆横截面上,轴力 N 的作用线与横截面垂直,且通过 横截面的形心,因此,分布在横截面上各点的应力只有正应力。 为计算正应力 ,可首先考查杆件在受力后表面上的变形情况, 并由表及里地推出反映杆件内部变形情况的几何关系,再根据力与变 形间的物理关系,得到应力在截面上的变化规律,最后再通过应力与 内力的静力学关系,得到应力的计算公式。下面就以上述方法,来推 导等直拉(压)杆横截面上的正应力计算公式。 1. 几何方面 P P 1 2 1 2 根据实验现象,提出如下著名的平面假设:变形前原为平面的横 截面,变形后仍保持为平面。 由这一假设可以推断,拉杆所有纵向纤维的伸长相等。即,拉杆 在其任意两个横截面之间的伸长变形是均匀的。 2. 物理方面 应力是伴随着变形同时产生的,且与杆的变形程度有关。既然各 点的变形程度相同,则我们可以认为,横截面上各点的正应力也是相 等的。 3. 静力学方面 根据静力学求合力的方法 = = = = A A N dN dA dA A

即得拉杆横截面上正应力σ的计算公式 A 式中N为轴力,A为杆的横截面面积。对压杆,此式同样适用。 常用的应力单位为:Pa、kPa、MPa、GPa。其中lPa=lN/m2、lkPa=l0 Pa、1MPa=10的Pa、1Gpa=l09Pa。 正应力的符号规定:以拉为正,以压为负。 必须指出,作用在杆件上的轴向外力,一般是外力系的静力等效 力系,在外力作用点附近的应力比较复杂,并非均匀分布。但圣唯南 原理指出:“力作用于杆端方式的不同,只会使与杆端距离不大于杆的 横截面尺寸的范围内的应力分布受到影响”。根据这一原理,除 了外力作用点附近以外,都可用上式计算应力。 当等直杆受几个轴向外力作用时,杆内的最大正应力为 A 最大轴力所在横截面称为危险截面,危险截面上的正应力称为最大工 作应力。 、拉(压)杆斜截面上的应力 由平衡方程ΣX=O,可得斜截面Kk上的内力 N。=p 仿照横截面上正应力分布规律的分析过程,同样可得到斜截面上各点 处的总应力P。是均匀分布且与杆轴平行的结论。设斜截面kk的外法 线n与杆轴线的夹角为,则横截面面积A=Acosα,于是有
即得拉杆横截面上正应力 的计算公式 A N = 式中 N 为轴力,A 为杆的横截面面积。对压杆,此式同样适用。 常用的应力单位为:Pa、kPa、MPa、GPa。其中 1Pa=1N/m2、1kPa=103 Pa、1MPa=106 Pa、1 Gpa=109 Pa。 正应力的符号规定:以拉为正,以压为负。 必须指出,作用在杆件上的轴向外力,一般是外力系的静力等效 力系,在外力作用点附近的应力比较复杂,并非均匀分布。但圣唯南 原理指出:“力作用于杆端方式的不同,只会使与杆端距离不大于杆的 横截面尺寸的范围内的应力分布受到影响”。根据这一原理,除 了外力作用点附近以外,都可用上式计算应力。 当等直杆受几个轴向外力作用时,杆内的最大正应力为 A Nmax max = 最大轴力所在横截面称为危险截面,危险截面上的正应力称为最大工 作应力。 三、拉(压)杆斜截面上的应力 由平衡方程 ΣX = 0,可得斜截面 k-k 上的内力 N = P 仿照横截面上正应力分布规律的分析过程,同样可得到斜截面上各点 处的总应力 p 是均匀分布且与杆轴平行的结论。设斜截面 k-k 的外法 线 n 与杆轴线的夹角为 ,则横截面面积 A = A cos ,于是有 k k P p P P P k k p