
一、广义胡克定律 1、单拉压的应力-应变关系 -E 8 8'=-l8 2、纯剪的应力-应变关系 Y=- ,0(i=x,y,z) Y=Y0
1、单拉压的应力--应变关系 ε µε σ ε ′ = − = E 2、纯剪的应力--应变关系 G τ γ = 0 (i x,y,z) ε i≈ = γ yz =γ zx ≈0 σ x y z τx y 一、 广义胡克定律

3、复杂状态下的应力--应变关系 共有六个独立得分量 小变形情况下,认为o引起6,x引起y Ox 2 依叠加原理,得: 61 X
3、复杂状态下的应力 --- 应变关系 依叠加原理,得: x y z σz σy τxy σx 小变形情况下,认为σ引起ε, τ 引起γ x y z τxy x y z σz σy σx = + 共有六个独立得分量
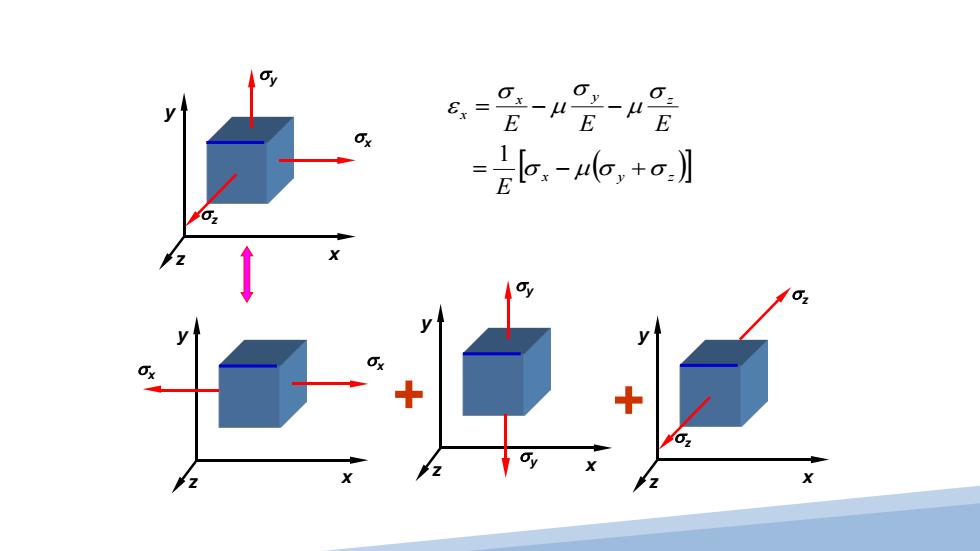
8x= E E 2k.-6,+a】 y
[ ( )] x y z x y z x EE E E σ µ σ σ σ µ σ µ σ ε = − + = − − 1 x y z σz σx σy + + x y z σ σx x x y z σyσy x y z σz σz
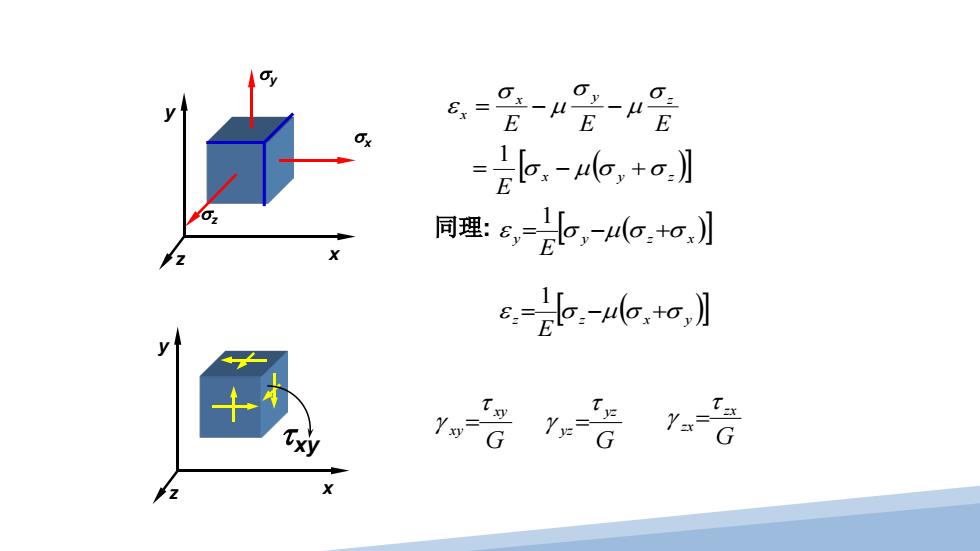
8x= E =2-h6,+o】 同理:£,,6o小 e--o,o,月 ro= G G
[ ( )] x y z x y z x E E E E σ µ σ σ σ µ σ µ σ ε = − + = − − 1 x y z τxy x y z σz σx σy [ ( )] y y z x E ε = σ −µ σ +σ 1 [ ( )] z z x y E ε = σ −µ σ +σ 1 G xy xy τ γ = G yz yz τ γ = G zx zx τ γ = 同理:
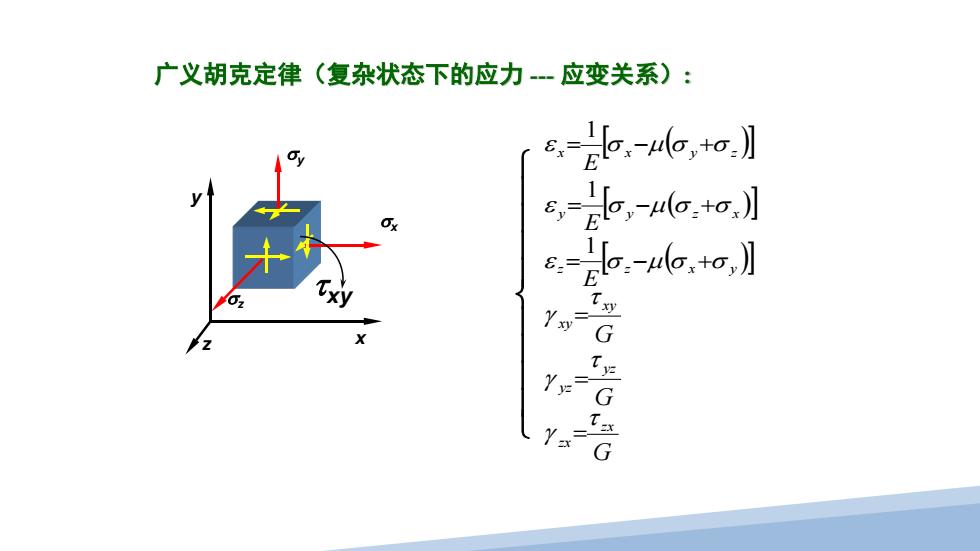
广义胡克定律(复杂状态下的应力--应变关系): 8,l,a】 -g,hao】 c-o+o,】 G Y= G Y G
广义胡克定律(复杂状态下的应力 --- 应变关系): [ ( )] y y z x E ε = σ −µ σ +σ 1 [ ( )] z z x y E ε = σ −µ σ +σ 1 G xy xy τ γ = G yz yz τ γ = G zx zx τ γ = [ ( )] x x y z E ε = σ −µ σ +σ 1 x y z σz σy τxy σx
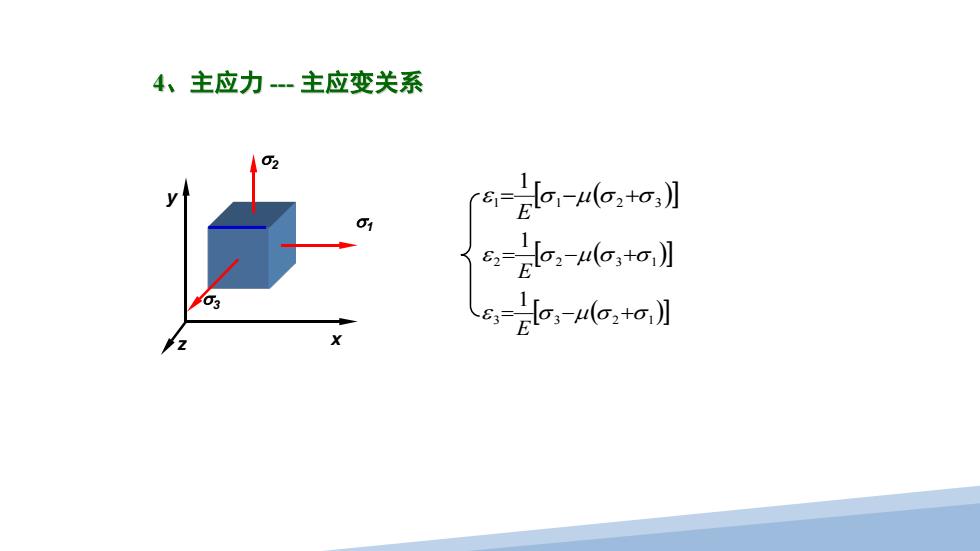
4、主应力-主应变关系 02 e2ar-o,to】 =,u6,to,】 6,2oo,to】
x y z σ3 σ1 σ2 [ ( )] 2 2 3 1 1 ε = σ −µ σ +σ E [ ( )] 3 3 2 1 1 ε = σ −µ σ +σ E [ ( )] 1 1 2 3 1 ε = σ −µ σ +σ E 4、主应力 --- 主应变关系

二、强度理论的概念 1、基本变形下强度条件的建立 FNma ≤[o](拉压) (正应力强度条件) M ≤[o] (弯曲) W FS' ≤[] (剪切) bI. (切应力强度条件) ≤[] (扭转) W
二、 强度理论的概念 1、基本变形下强度条件的建立 max max [ ] FN A σ σ = ≤ (拉压) [ ] max σ max = ≤ σ W M (弯曲) [ ] * max τ = ≤ τ z s z bI F S (剪切) τ max = ≤ [τ ] (扭转) p n W M (正应力强度条件) (切应力强度条件)
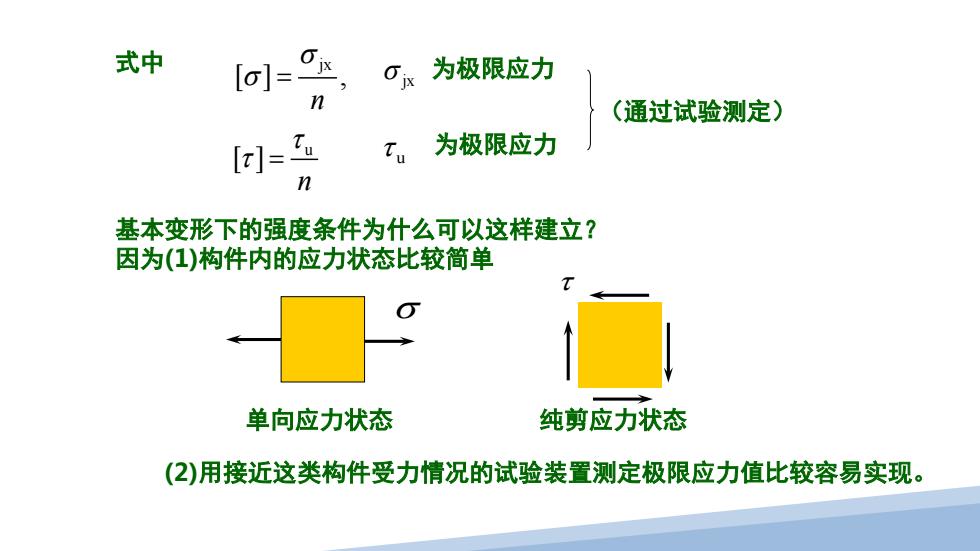
式中 6 [o]= Oi 为极限应力 n (通过试验测定) 为极限应力 n 基本变形下的强度条件为什么可以这样建立? 因为(1)构件内的应力状态比较简单 单向应力状态 纯剪应力状态 (2)用接近这类构件受力情况的试验装置测定极限应力值比较容易实现
式中 jx [] , n σ σ = σ jx 为极限应力 u [ ] n τ τ = τ u 为极限应力 (通过试验测定) 基本变形下的强度条件为什么可以这样建立? 因为(1)构件内的应力状态比较简单 σ τ 单向应力状态 纯剪应力状态 (2)用接近这类构件受力情况的试验装置测定极限应力值比较容易实现
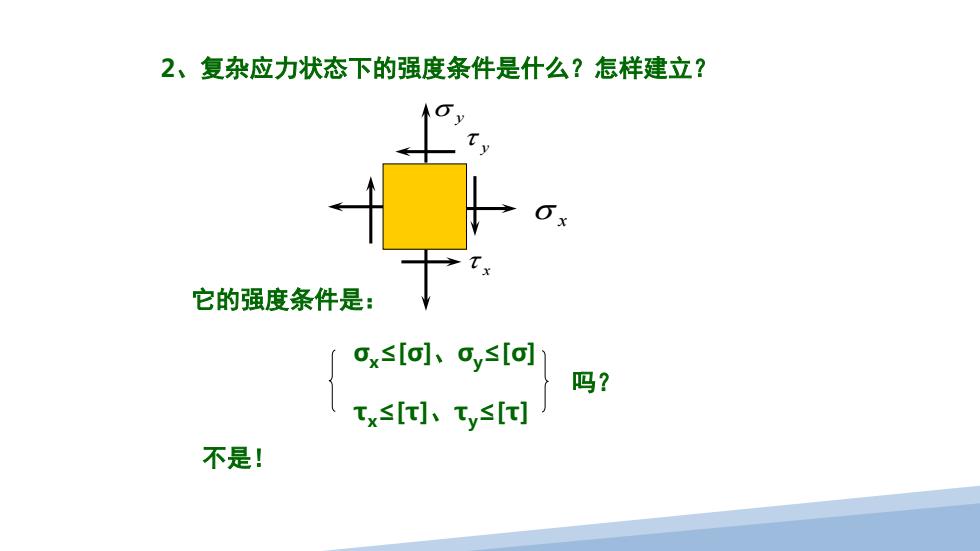
2、复杂应力状态下的强度条件是什么?怎样建立? 它的强度条件是: Icx≤[o]、cy[o] 吗? tx≤[t]、Tv≤[] 不是!
2、复杂应力状态下的强度条件是什么?怎样建立? σ x x τ y τ σ y 它的强度条件是: σx≤[σ]、σy≤[σ] 吗? τx≤[τ]、τy≤[τ] 不是!

2、复杂应力状态下(二向或三向)的强度条件的建立: 试验的方法不再行得通,故人们对材料的破坏形 式和破坏原因进行分析,提出假设,利用轴向拉压试 验或纯剪切试验得出得结果,共同建立普遍适用的强 度条件。 3、关于强度理论的假设: 无论是简单或复杂的应力状态,引起失效的因素是相 同的,(应力、应变或应变能密度其中之一引起),和应 力状态无关,取决于材料本身。 不同的强度理论对引起失效的因素有不同的看法,所 以至今为止,出现了很多种强度理论,但每种强度理论都 有它适用的局限性,大致分为经典强度理论和现代强度理 论
2、复杂应力状态下(二向或三向)的强度条件的建立: 试验的方法不再行得通,故人们对材料的破坏形 式和破坏原因进行分析,提出假设,利用轴向拉压试 验或纯剪切试验得出得结果,共同建立普遍适用的强 度条件。 3、关于强度理论的假设: 无论是简单或复杂的应力状态,引起失效的因素是相 同的,(应力、应变或应变能密度其中之一引起),和应 力状态无关,取决于材料本身。 不同的强度理论对引起失效的因素有不同的看法,所 以至今为止,出现了很多种强度理论,但每种强度理论都 有它适用的局限性,大致分为经典强度理论和现代强度理 论