
目录 CONTENTS ∠1 应力分析 2 切应力互等定理 3 剪切胡克定律
123 应力分析 切应力互等定理 剪切胡克定律 目录 CONTENTS
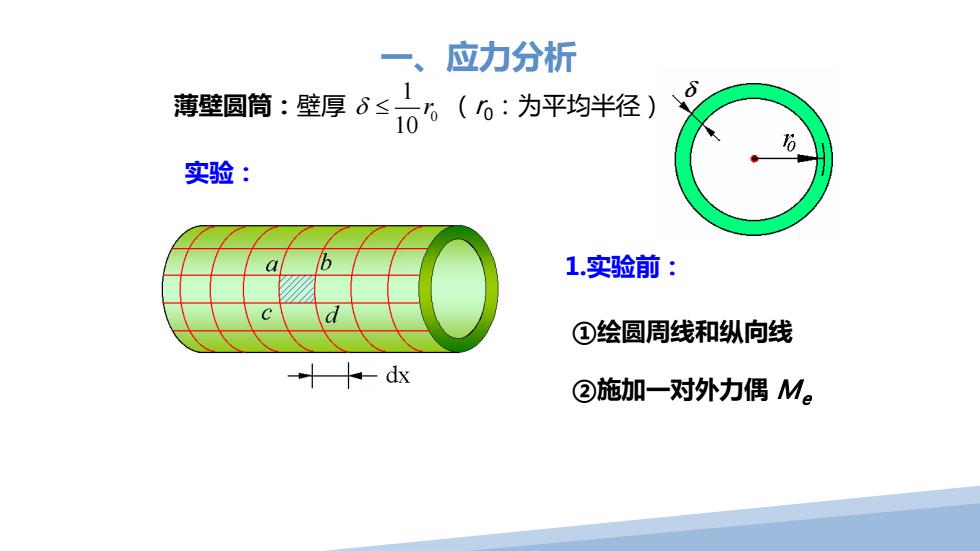
一、应力分析 1 薄壁圆筒:壁厚δ≤。6(0:为平均半径) 10 实验: 1.实验前: ①绘圆周线和纵向线 十dx ②施加一对外力偶M
薄壁圆筒:壁厚 0 1 10 δ ≤ r (r0:为平均半径) 实验: 1.实验前: ①绘圆周线和纵向线 ②施加一对外力偶 Me 一、应力分析
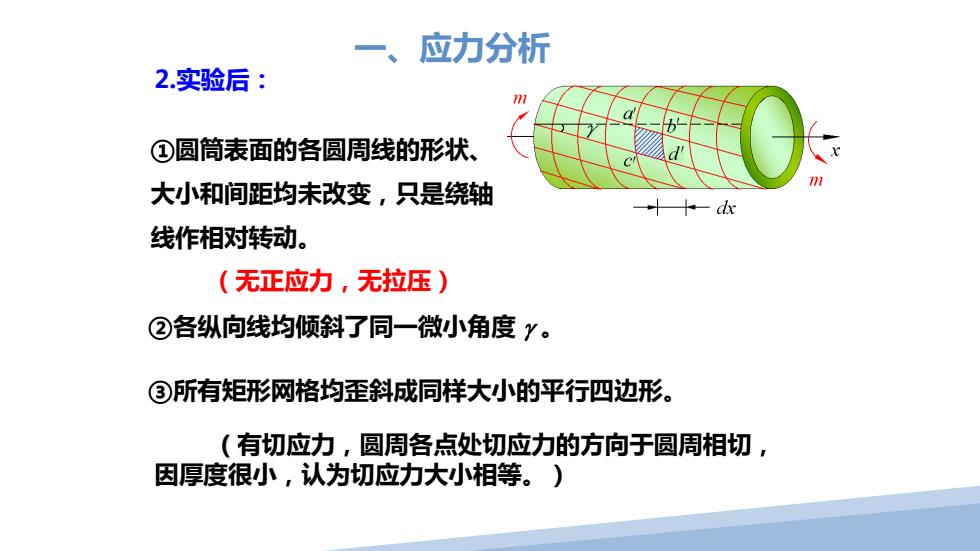
一、 应力分析 2.实验后: ①圆筒表面的各圆周线的形状、 大小和间距均未改变,只是绕轴 十-dx 线作相对转动。 (无正应力,无拉压) ②各纵向线均倾斜了同一微小角度Y。 ③所有矩形网格均歪斜成同样大小的平行四边形。 (有切应力,圆周各点处切应力的方向于圆周相切, 因厚度很小,认为切应力大小相等。)
2.实验后: ②各纵向线均倾斜了同一微小角度 γ 。 ①圆筒表面的各圆周线的形状、 大小和间距均未改变,只是绕轴 线作相对转动。 (无正应力,无拉压) ③所有矩形网格均歪斜成同样大小的平行四边形。 一、应力分析 (有切应力,圆周各点处切应力的方向于圆周相切, 因厚度很小,认为切应力大小相等。)
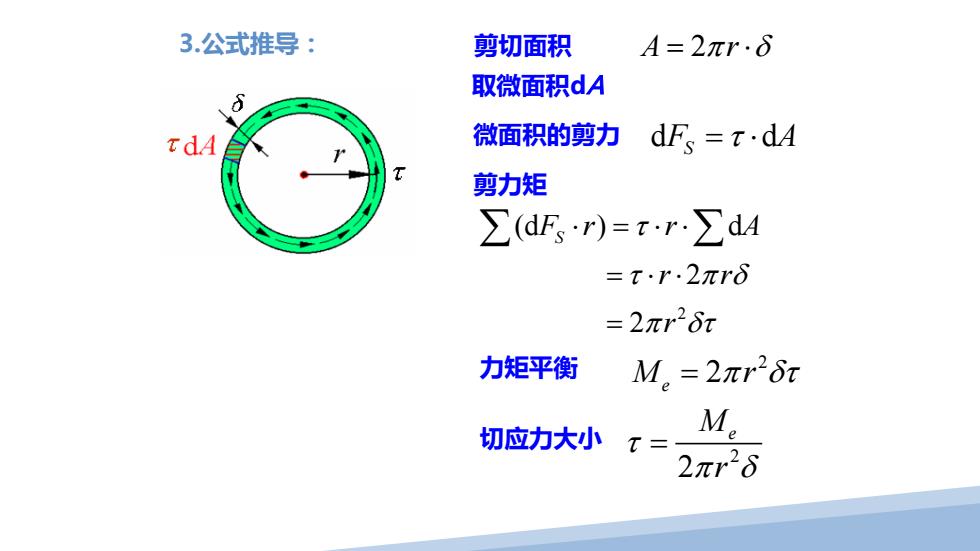
3.公式推导: 剪切面积 A=2πr.6 取微面积dA 微面积的剪力 dF=t·dA 剪力矩 ∑dFr)=tr.∑dA =t.r.2πrδ =2πr26a 力矩平衡 M。=2πr26z 切应力大小 M。 t= 2πr26
剪切面积 微面积的剪力 A r = ⋅ 2π δ d d F A S = ⋅ τ 剪力矩 力矩平衡 2 2 M r e = π δτ 切应力大小 2 2 M e r τ π δ = 2 (d ) d 2 2 Fr r A S r r r τ τ πδ π δτ ⋅ = ⋅⋅ = ⋅⋅ = ∑ ∑ 取微面积dA 3.公式推导:
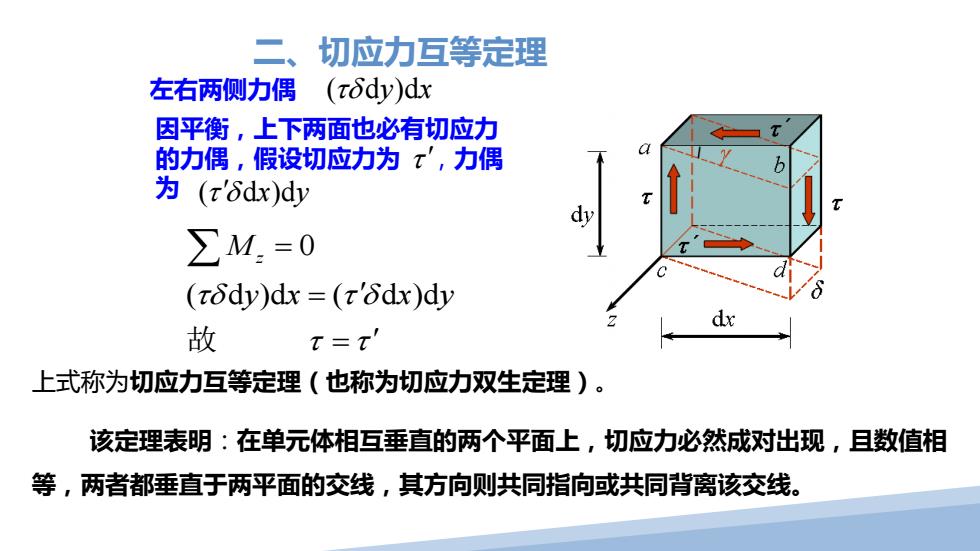
二 切应力互等定理 左右两侧力偶 (tδdy)dx 因平衡,上下两面也必有切应力 的力偶,假设切应力为τ',力偶 为(x'6dx)dy ∑M:=0 (tδdy)dx=(x6dx)dy d 故 t=t 上式称为切应力互等定理(也称为切应力双生定理)。 该定理表明:在单元体相互垂直的两个平面上,切应力必然成对出现,且数值相 等,两者都垂直于两平面的交线,其方向则共同指向或共同背离该交线
0 ( d )d ( d )d M z τδ τ δ yx xy τ τ = = ′ = ′ ∑ 故 上式称为切应力互等定理(也称为切应力双生定理)。 该定理表明:在单元体相互垂直的两个平面上,切应力必然成对出现,且数值相 等,两者都垂直于两平面的交线,其方向则共同指向或共同背离该交线。 左右两侧力偶 ( d )d τδ y x 因平衡,上下两面也必有切应力 的力偶,假设切应力为 ,力偶 为 τ ′ ( d )d τ δ′ x y 二、切应力互等定理
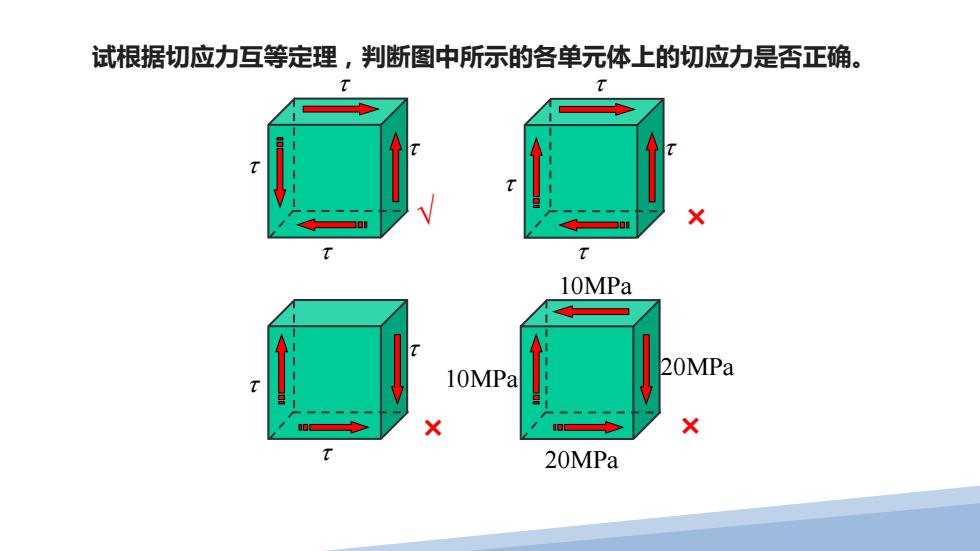
试根据切应力互等定理,判断图中所示的各单元体上的切应力是否正确。 T T X 7 10MPa 10MPa 20MPa X 20MPa
试根据切应力互等定理,判断图中所示的各单元体上的切应力是否正确。 τ τ τ τ τ τ τ τ 10MPa 20MPa 10MPa 20MPa τ τ τ √ × × ×
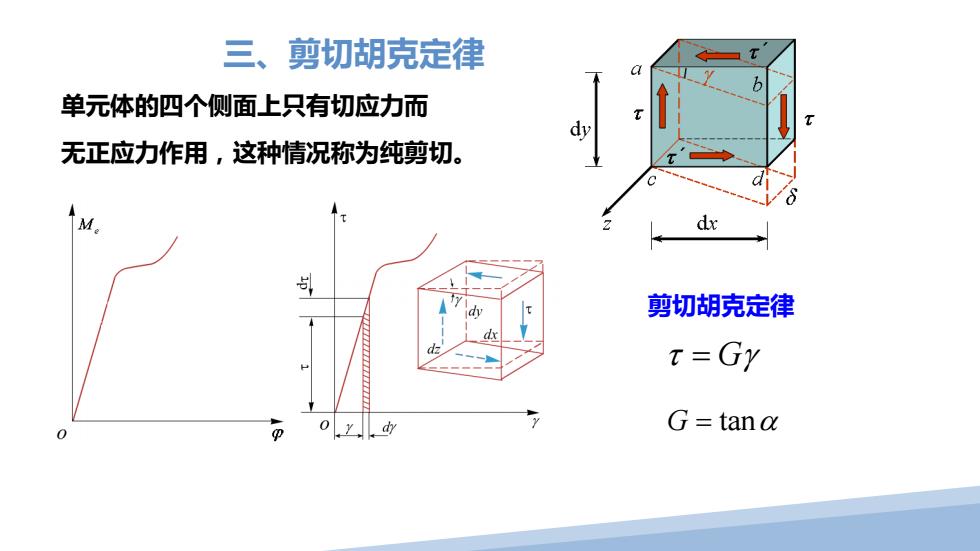
三、剪切胡克定律 a 单元体的四个侧面上只有切应力而 d 无正应力作用,这种情况称为纯剪切。 dx 剪切胡克定律 t=Gy 0 G=tana
单元体的四个侧面上只有切应力而 无正应力作用,这种情况称为纯剪切。 三、剪切胡克定律 剪切胡克定律 τ γ = G G = tanα

剪切胡克定律 t=G·Y 式中:G是材料的一个弹性常数,称为剪切弹性模量,因y无量纲,故G的量纲 与x相同。 剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三个常数。对各向同性 材料,这三个弹性常数之间存在下列关系: E G= 21+4) 可见,在三个弹性常数中,只要知道任意两个,第三个量就可以推算出来
式中:G 是材料的一个弹性常数,称为剪切弹性模量,因 γ 无量纲,故 G 的量纲 与 τ 相同。 剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三个常数。对各向同性 材料,这三个弹性常数之间存在下列关系: 可见,在三个弹性常数中,只要知道任意两个,第三个量就可以推算出来。 剪切胡克定律