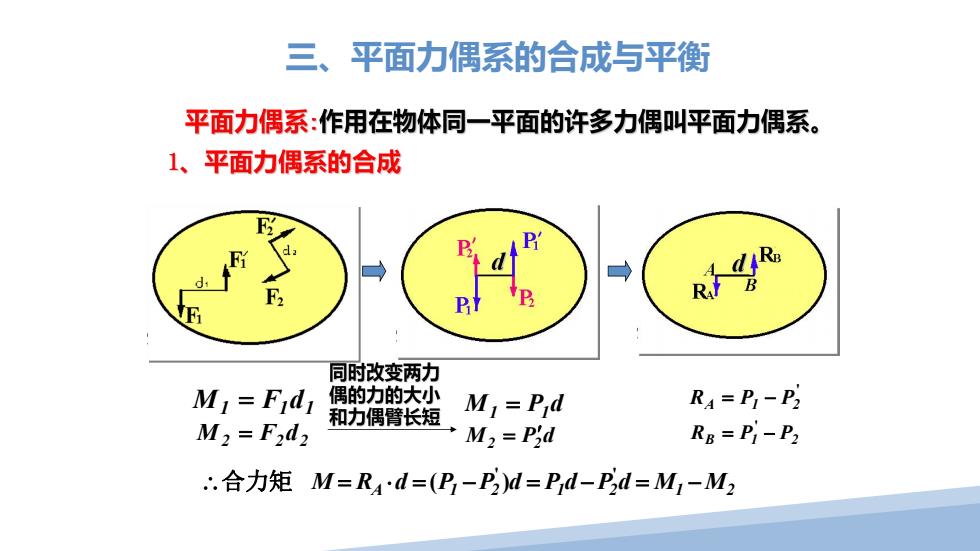
三、平面力偶系的合成与平衡 平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系。 1、平面力偶系的合成 R 同时改变两力 M=Fd 偶的力的大小 M=Pd R4=PI-P2 和力偶臂长短 M2=F2d2 M2=Pid RB=PI-P2 .合力矩M=R4d=(D-P)M=Pd-Pd=M1-M2
' RA P1 P2 RB P1 P2 ' 1 1 1 M F d 2 2 2 M F d M P d 1 1 M P d 2 2 三、平面力偶系的合成与平衡 M RA d P1 P2 d P1d P2d M1 M2 ' ' 合力矩 ( )

结论: 在同平面内的任意个力偶(力偶系),其合成的结果,还是一个力偶,合 力偶矩为各力偶矩的代数和。 M=M,+M,++M,=2M, 2、平面力偶系的平衡条件: 平面力偶系平衡的充要条件是:所有各力偶矩的代数和等于零。 4=0 i=l
n i 1 M M 1 M 2 M n M i M 0 n i 1 i

【例1】梁AB两端各作用一力偶,力偶矩的大小为M,=I7kWm,M2=27.5kWm, 转向如图。梁长l=6m,梁的重量不计,试求:A、B两处的约束力。 M 解:受力图如右图: M=0,M1-M2+F,1=0 a) F=F =1.75kN b)
【 】梁AB两端各作用一力偶,力偶矩的大小为M1=17kN·m, M2=27.5kN·m, 转向如图。梁长l=6m,梁的重量不计,试求:A、B两处的约束力。 解:受力图如右图: 0, 0 Mi M1 M2 FA l FA FB 1.75kN

【例2】已知M,=2kNm,OA=r=0.5m,0=30°: 求:平衡时的M,及铰链O,B处的约束力. 解:取轮,由力偶只能由力偶平衡的性质,画受力图。 ∑M=0M1-F4rsin0=0 解得F。=F=8kN 取杆BC,画受力图。 ∑M=0 Fr。-M,=0 sin 解得 M,=8kN.m F=F=8kN
取轮,由力偶只能由力偶平衡的性质,画受力图。 取杆 B C ,画受力图。 解:

本章小结 1.掌握力对点的矩的计算 2.了解力偶概念,掌握平面力偶的性质 3.重点掌握平面力偶系平衡问题的计算
1.掌握力对点的矩的计算 2.了解力偶概念,掌握平面力偶的性质 3.重点掌握平面力偶系平衡问题的计算 本 章 小 结