扭转破坏 塑性材料 脆性材料
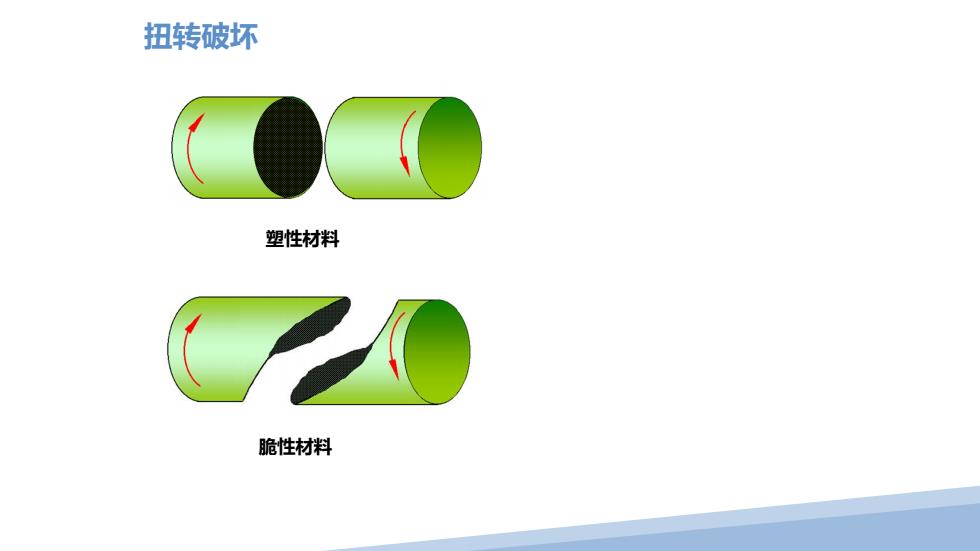
扭转破坏 塑性材料 脆性材料

扭转强度条件 I max max s[] 已知T、和D,[t]校核强度 w, 已知T和[], 设计截面 W= πD3 16 已知D和[t],确定许可载荷 对于变截面杆,如阶梯轴等,W,不是常量,Tmax并不一定发生在 扭矩为Tx的截面处,要综合考虑。 正如拉压情况,变截面杆Omax并不一定发生 在最大内力位置
对于变截面杆,如阶梯轴等, 不是常量, 并不一定发生在 扭矩为 的截面处,要综合考虑。 Wt max τ Tmax 扭转强度条件 [ ] max max t T W τ τ = ≤ 3 16 t D W π = 已知 T 、和 D, [τ ]校核强度 已知 T 和 [τ ] , 设计截面 已知 D 和 [τ ] ,确定许可载荷 正如拉压情况,变截面杆 并不一定发生 在最大内力位置。 σ max
强度条件 即 W 1.等截面圆轴:(W为常量) 2.阶梯形圆轴: Me3 620Nm 780N-m 1400Nm Me3 (+) 620Nm 1400Nm Mel [小 W (p)
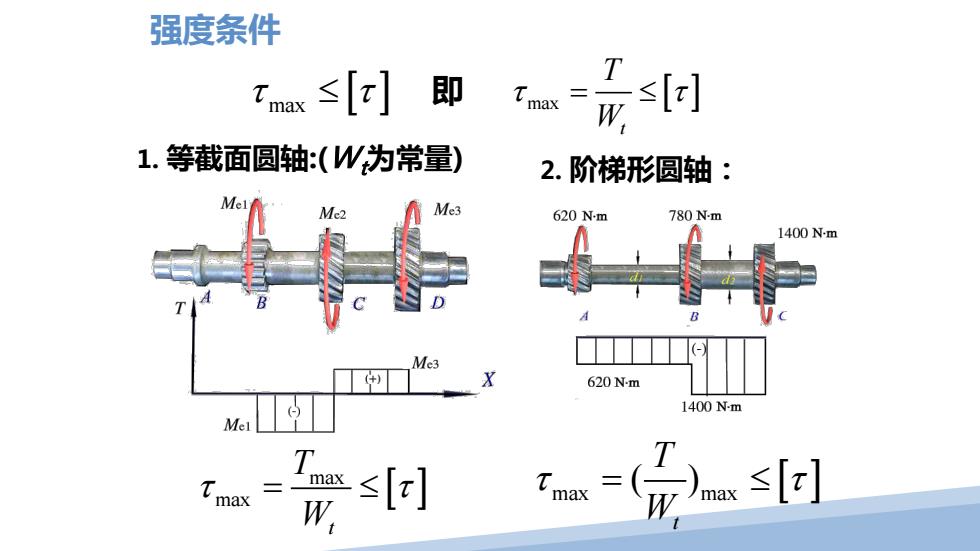
1. 等截面圆轴:(Wt 为常量) 2. 阶梯形圆轴: 强度条件 τ τ max ≤ [ ] max [ ] t T W 即 τ τ = ≤ [ ] max max t T W τ τ = ≤ max ( )max [ ] t T W τ τ = ≤

例1 汽车传动轴,外径D=90mm,壁厚δ=2.5mm, 最大扭矩T=1.5kN.m材料的[t]=60MPa。 试校核轴的扭转强度。 (a) 传动钠 解:根据截面尺寸计算抗扭截面系数 (b) d90-2×2.5 Q= =0.944 TD3 D 90 1-a4)=π(90x103m)3 (1-0.9444)=2.94×10-5m3 16 16 轴的最大切应力为 T 1.5×103 2.94x10=51x10Pa=51MPa<[r] 传动轴满足扭转强度条件
max t T W τ = 轴的最大切应力为 例1 汽车传动轴,外径 ,壁厚 , 最大扭矩 材料的 。 试校核轴的扭转强度。 D = 90mm δ = 2.5mm T = ⋅ 1.5 kN m [τ ] = 60MPa 解:根据截面尺寸计算抗扭截面系数 d D α = 3 4 (1 ) 16 t D W π = −α 传动轴满足扭转强度条件 90 2 2.5 0.944 90 − × = = 3 3 4 5 3 (90 10 m) (1 0.944 ) 2.94 10 m 16 π − × − = − =× 3 6 5 1.5 10 51 10 Pa 51 MPa 2.94 10− × = =× = × < [τ ]

例2 若将上例的传动轴改为实心轴,要求与原来的空心轴 强度相同,试确定其直径,并比较两者的重量。 解:由强度相同,又x=T,即 传动钠 W 要求抗扭截面系数相等 (b) W=W,2 (抗扭截面系数相等) πD_πD 1616 (1-a)◆D=53.1mm
例2 若将上例的传动轴改为实心轴,要求与原来的空心轴 强度相同,试确定其直径,并比较两者的重量。 W W t t 1 2 = 3 3 1 4 (1 ) 16 16 π D π D = −α 1 D = 53.1 mm (抗扭截面系数相等) 解:由强度相同,又 ,即 t T W τ = 要求抗扭截面系数相等

比较两者的重量,用两者的截面积比较: 实心截面积 4Q 4 空心截面积 4= π(D2-d2) 4 重量之比等于截面积之比 空心4D2-d2902-85 -=0.31 实心AD2 53.12 (减轻重量,节约材料)
实心截面积 比较两者的重量,用两者的截面积比较: 2 1 1 4 D A π = 空心截面积 2 2 2 ( ) 4 D d A π − = 重量之比等于截面积之比 22 2 2 2 2 2 1 1 90 85 0.31 53.1 A D d A D − − = = = = 空心 实心 (减轻重量,节约材料)
切应力分布 Lmax max max max (实心截面) (空心截面) 工程上采用空心截面构件:提高强度,节约材料,重量轻,结构轻便,应用 广泛。 轴心附近应力小,材料没有充分发挥作用(大材小用),将轴心附近材料向 边缘移置
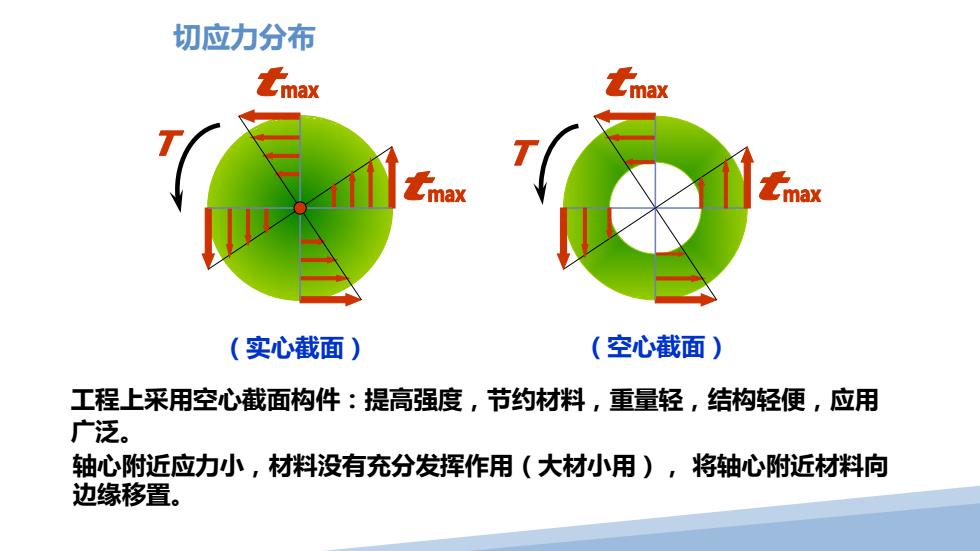
切应力分布 (实心截面) (空心截面) 工程上采用空心截面构件:提高强度,节约材料,重量轻,结构轻便,应用 广泛。 轴心附近应力小,材料没有充分发挥作用(大材小用), 将轴心附近材料向 边缘移置
例3 已知:P=7.5kW,n=100r/min,最大切应力不得超过40 MPa,空心圆轴的内外直径之比a=0.5。 求:实心轴的直径d1和空心轴的外直径D2
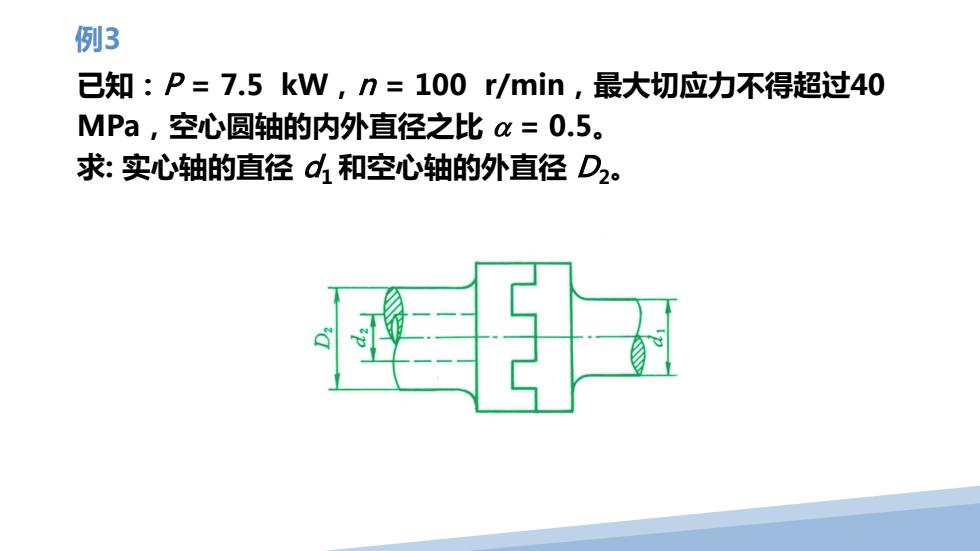
已知:P = 7.5 kW,n = 100 r/min,最大切应力不得超过40 MPa,空心圆轴的内外直径之比 α = 0.5。 求: 实心轴的直径 d1 和空心轴的外直径 D2。 例3

解:首先由轴所传递的功率计 算作用在轴上的扭矩 M.=7=9549×2 n =9549× 7.5 =716.2N.m 100 实心轴: T 16T T axI πd s[] W 16T 16×716.2 d =0.045m=45mm π×40×106
解:首先由轴所传递的功率计 算作用在轴上的扭矩 实心轴: 3 1 16T π d = ≤ [τ ] 3 6 16 716 2 0 045 m 45 mm π 40 10 × = = = × × .

空心轴: T 16T W2 xDi-as[] 16T 16×716.2 D≥j0-a)πx40x10×0-05 .=0.046m=46mm d2=0.5D2=23mm 两轴的横截面面积之比为: A2_D-d6462-232 =0.783 A d 452
空心轴: max 2 t 2 T W τ = [ ] 3 2 4 16 (1 ) T D πτ α ≥ − 2 2 d D = = 0.5 23mm 两轴的横截面面积之比为: 3 4 2 16 (1 ) T π α D = − ≤ [τ ] 3 6 4 16 716.2 0.046m 46mm π 40 10 (1 0.5 ) × = = = × × ×−