
6.6轴向拉压时的强度计算 失效:由于材料的力学行为而使构件丧失正常工作能力 强度失效:由于断裂或屈服引起的失效 刚度失效:由于过量的弹性变形引起的失效 屈曲失效:由于平衡构形的突然转变而引起的失效
6.6 轴向拉压时的强度计算 失效:由于材料的力学行为而使构件丧失正常工作能力 强度失效:由于断裂或屈服引起的失效 刚度失效:由于过量的弹性变形引起的失效 屈曲失效:由于平衡构形的突然转变而引起的失效

强度失效:断裂、塑性变形、压溃、压扁 极限应力-材料破坏时的应力o:O、C.2、C 失效判据:OC、C.2、C 许用应力~保证构件安全可靠工作所容许的最大应力 n. 安全系数:n、nb >材质情况均匀?各向同性) 工作应力:σ >载荷情况(近似?稳定?) 强度条件:σ= s[a] >计算模型(简化?) A >重要性、制造难度 >自重、机动性 >强度校核 >查规定、规范或设计手册 >截面设计 >确定许可载荷 塑性:n、=1.2~2.5 脆性n较大? 脆性:,=23.5,3-9
极限应力-材料破坏时的应力σ u:σs、σ0.2、σb 安全系数:ns、nb 强度失效:断裂、塑性变形、压溃、压扁 [ ] s s n σ σ = 许用应力-保证构件安全可靠工作所容许的最大应力 [ ] b b n σ σ = 工作应力:σ [ ] FN A 强度条件: σ σ = ≤ 强度校核 截面设计 确定许可载荷 材质情况(均匀?各向同性?) 载荷情况(近似?稳定?) 计算模型(简化?) 重要性、制造难度 自重、机动性 查规定、规范或设计手册 失效判据:σ=σs、σ0.2、σb 塑性:ns=1.2~2.5 脆性n较大? 脆性:nb=2~3.5,3~9

例6-6图示铸铁杆横截面积A=50mm2,许用拉应力[c=42MPa,许用压应力 [o=100MPa。校核其强度。 2kN 3kN 3kN 解:(1)画轴力图 B (2)拉压校核: FB-2×I0 F Pa A 50×10-6 2kN =40MPa<[o,] 4×103 1kN Pa 50×106 4kN A =80MPa<[o] 满足强度条件
例6-6 图示铸铁杆横截面积A=50mm2,许用拉应力[σt ]=42MPa,许用压应力 [σc]=100MPa。校核其强度。 解:(1)画轴力图 (2)拉压校核: 3 max 6 2 10 Pa 50 10 40 MPa<[ ] σ σ − × = = × = NAB t t F A A B C D 2kN 3kN 满足强度条件。 3kN FN x 2kN 4kN 3 1kN c max 6 4 10 Pa 50 10 80 MPa<[ ] σ σ − × = = × = NCD c F A
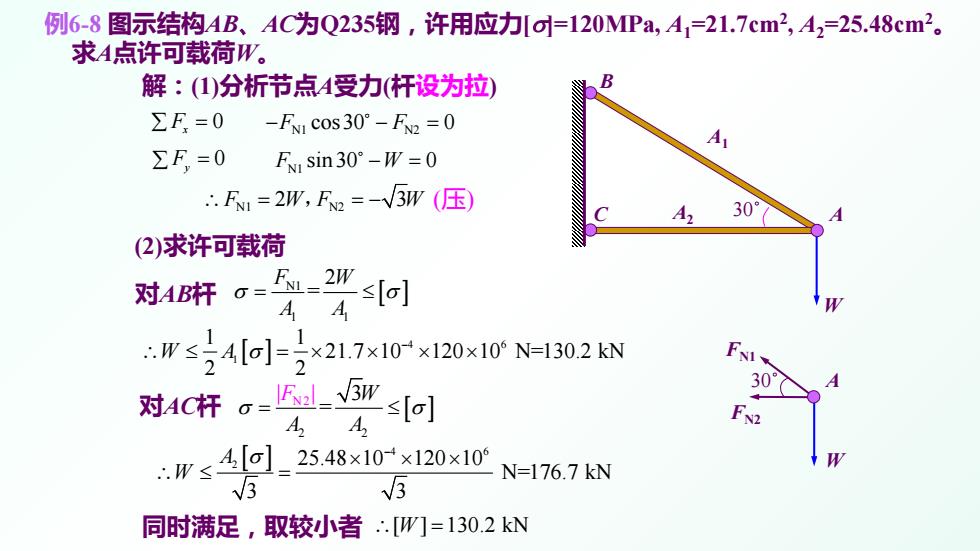
例6-8图示结构4AB、AC为Q235钢,许用应力[d=120MPa,A1=21.7cm2,A2=25.48cm2。 求A点许可载荷W。 解:(①)分析节点4受力(杆设为拉) ∑F=0 -FN1cos30°-F2=0 ∑F=0 F,sin30°-W=0 ∴.F1=2W,F2=-V3W(压) 30 (2)求许可载荷 对AB开。==2 s[] W≤24a]=2×21.7x10×120x10N1302kN 对AC杆 a=IFel_v3W s[o] ..Ws 4,[o]_25.48×10-×120×10 N=176.7kN 3 √3 同时满足,取较小者∴[W]=130.2kN
[ ] 4 6 2 25.48 10 120 10 N=176.7 kN 3 3 A W σ − × ×× ∴≤ = 例6-8 图示结构AB、AC为Q235钢,许用应力[σ]=120MPa, A1=21.7cm2 , A2=25.48cm2 。 求A点许可载荷W。 C A A1 A2 (2)求许可载荷 30˚ B W 解:(1)分析节点A受力(杆设为拉) [ ] 4 6 1 1 1 21.7 10 120 10 N=130.2 kN 2 2 σ − ∴ ≤ =× × × × W A 0 ∑ F x = N1 N2 − −= F F cos30 0 0 ∑ F y = N1 F W sin 30 0 − = N1 N2 ∴ = =− F WF W 2 3 , 同时满足,取较小者 ∴ = [ ] 130.2 kN W 对AB杆 [ ] N1 1 1 2 = F W A A σ σ = ≤ 对AC杆 [ ] 2 N2 2 | | 3 = A A F W σ σ = ≤ A W FN1 FN2 30˚ (压)