4.2 平面一般力系向作用面内一点简化 一、 简化方法 = M=M() O:简化中心 = M=M(E) =元M=M,(匠) 中还? 丰矢、 主矩变否? =Σ=x 主矢 F=Σ M。=∑M,=ΣMo(E) 主矩 M。=ΣM() F 平面任意力系 平面汇交力系+平面力偶系 主矢+主矩
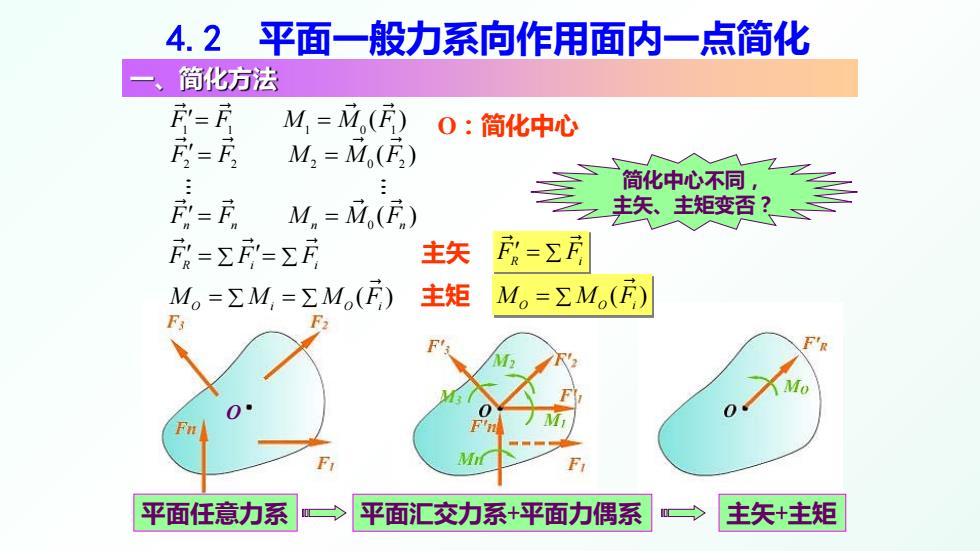
O 4.2 平面一般力系向作用面内一点简化 1 1 1 01 F F M MF ′ = = ( ) 2 2 2 02 F F M MF ′ = = ( ) 0 ( ) F F M MF nn n n ′ = = F FF Rii ′ ′ = = ∑ ∑ ( ) M M MF O i Oi = = ∑ ∑ 主矢 主矩 F F R i ′ = ∑ ( ) M MF O Oi = ∑ 简化中心不同, 主矢、主矩变否? 平面汇交力系+平面力偶系 主矢+主矩 O:简化中心 一、简化方法 平面任意力系
平面任意力系向作用面内任一点O简化,可得一个力和一个力偶。这个力等于该力 系的主矢,作用线通过简化中心0。这个力偶的矩等于该力系对于点O的主矩。 >主矢与简化中心的位置无关,主矩和简化中心的位置有关。 如何求主矢、主矩? F=∑F=∑F.=∑F F=ΣF=ΣF。=ΣF 主矢大小:F=V区F)+(②E)月 方向: cos(f房i=EE c0s(方=】 F 作用点: 作用于简化中心上 主矩: M。=∑Mo()
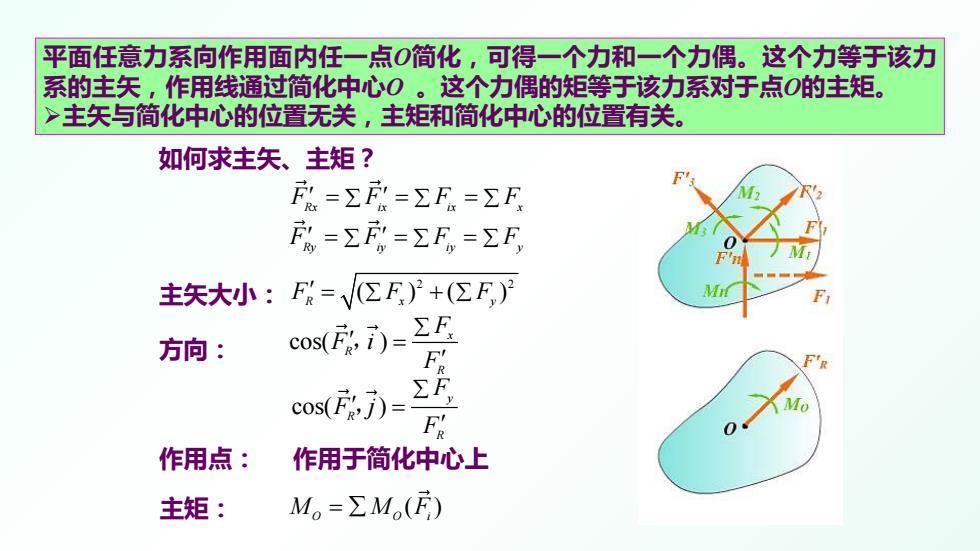
如何求主矢、主矩? 主矢大小: 方向: 作用点: 作用于简化中心上 主矩: F FFF Rx ix ix ∑∑∑ x ′ ′ = = = F FFF Ry iy iy ∑∑∑ y ′ ′ = = = ( ) M MF O Oi = ∑ cos( ) y R R F F j F ∑ ′ = ′ , cos( ) x R R F F i F ∑ ′ = ′ , 2 2 ( )( ) F FF Rxy ′ = + ∑ ∑ 平面任意力系向作用面内任一点O简化,可得一个力和一个力偶。这个力等于该力 系的主矢,作用线通过简化中心O 。这个力偶的矩等于该力系对于点O的主矩。 主矢与简化中心的位置无关,主矩和简化中心的位置有关
二 固定端约束 物体的一端完全固定在另一物体上,这种约束称为固定端约束。 比较:三种支座 ①滚动铰支 ②固定铰支 ③固定端
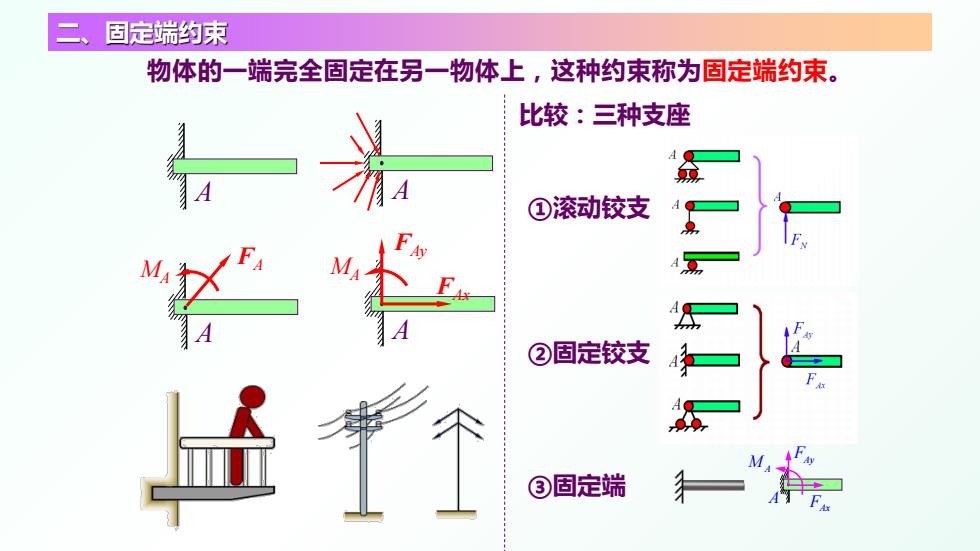
二、固定端约束 物体的一端完全固定在另一物体上,这种约束称为固定端约束。 A A A A MA FAy FAx M FA A ②固定铰支 ①滚动铰支 ③固定端 比较:三种支座 FAx M A A FAy