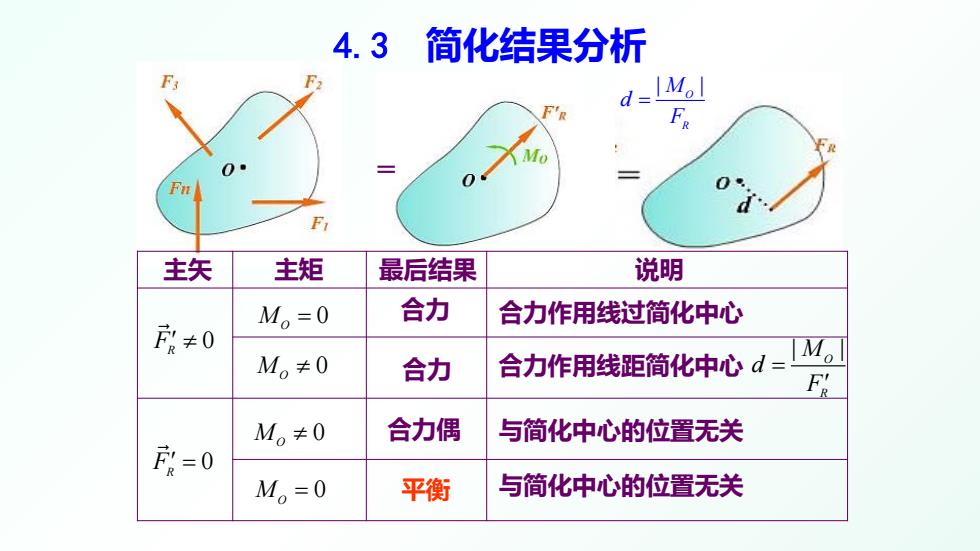
4.3简化结果分析 d=IMol \Mo 0 F 主矢 主矩 最后结果 说明 M。=0 合力 合力作用线过简化中心 ≠0 M。≠0 合力 合力作用线距简化中心d=M。 M。≠0 合力偶 与简化中心的位置无关 =0 M=0 平衡 与简化中心的位置无关
4.3 简化结果分析 = 主矢 主矩 最后结果 说明 合力 合力 合力作用线过简化中心 合力偶 平衡 与简化中心的位置无关 与简化中心的位置无关 0 FR ′ ≠ 0 FR ′ = 0 MO = 0 MO ≠ 0 MO ≠ 0 MO = 合力作用线距简化中心 | | O R M d F = ′ | | O R M d F =
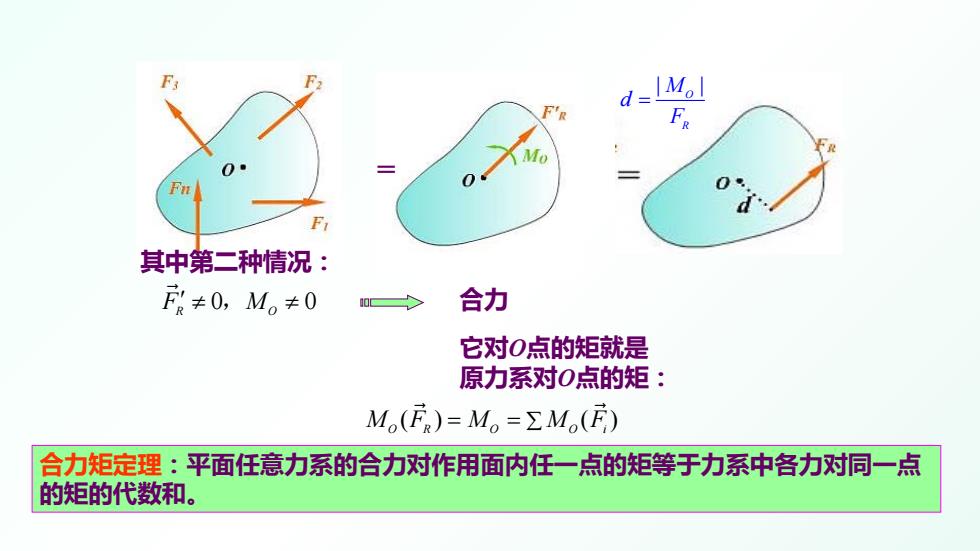
d=41 F'R Mo Fn F 其中第二种情况: F≠0,M。≠0 合力 它对O点的矩就是 原力系对O点的矩: M()=M。=ΣM() 合力矩定理:平面任意力系的合力对作用面内任一点的矩等于力系中各力对同一点 的矩的代数和
合力矩定理:平面任意力系的合力对作用面内任一点的矩等于力系中各力对同一点 的矩的代数和。 ( ) () MF M MF OR O Oi = = ∑ 其中第二种情况: 0 0 F M R O ′ ≠ ≠ , 合力 它对O点的矩就是 原力系对O点的矩: = | | O R M d F =
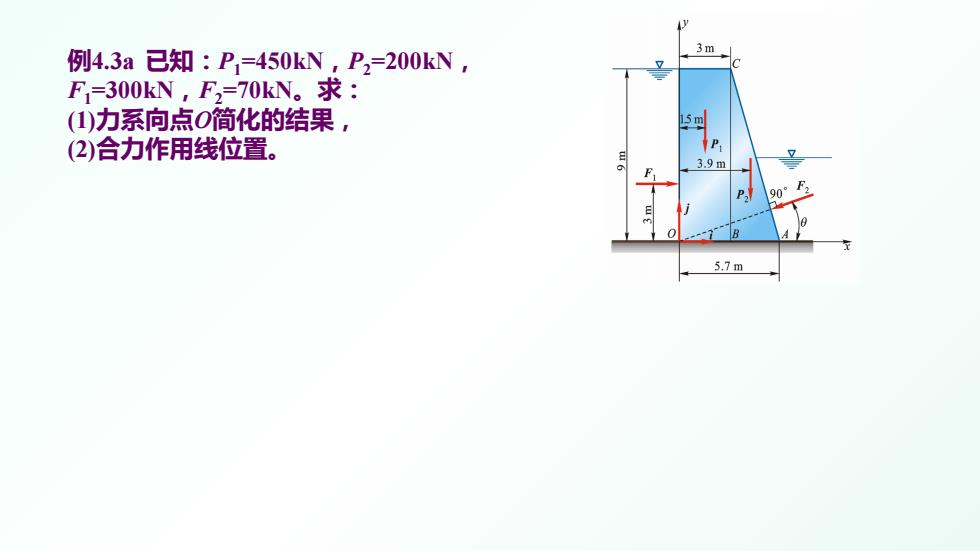
3m 例4.3a已知:P=450kN,P2=200kN, F=300kN,F2=70kN。求: (1)力系向点O简化的结果, 5m (2)合力作用线位置。 P 39m P 90 B 5.7m
例4.3a 已知:P1=450kN,P2=200kN, F1=300kN,F2=70kN。求: (1)力系向点O简化的结果, (2)合力作用线位置

解:()向0点简化,求主矢和主矩。 3m O=∠ACB=arctan =16.7 AB BC FR=F=F-F COs0=232.9kN 3.9m FR=>Fiy =-P-P-F sin0=-670.1kN 90 主矢大小F=V(区Fa)'+(区Fm)'-709.4k 5.7m 方向余弦c0s(位)=25=0,3283 FR cos(Fxj)- F2=-0.9446 F .∠(1)=-70.84° 0 主矢在第4象限,与.轴夹角-70.84 F'Ry 主矩 M。=∑M(F)=-3E-1.5P-3.9P=-2355kNm
解:(1)向O点简化, 求主矢和主矩。 主矢大小 方向余弦 主矩 11 2 M MF F P P o oi = =− − − =− ⋅ ∑ ( ) 3 1.5 3.9 2355 kN m cos 0.3283 ( ) ix R R F F i F ∑ ′ = = ′ , cos 0.9446 ( ) iy R R F F j F ∑ ′ = = − ′ , 1 2 F F PPF Ry iy ′ = =− − − =− ∑ sin 670.1kN θ arctan 16.7 AB ACB BC θ =∠ = = 1 2 F F FF Rx ix ′ = =− = ∑ cos 232.9kN θ 主矢在第4象限,与x轴夹角-70.84˚ (F i R 70.84 ) ∴∠ = − ′ , ( ) ( ) 2 2 FF F R ′ = += ∑ ∑ ix iy 709.4 kN
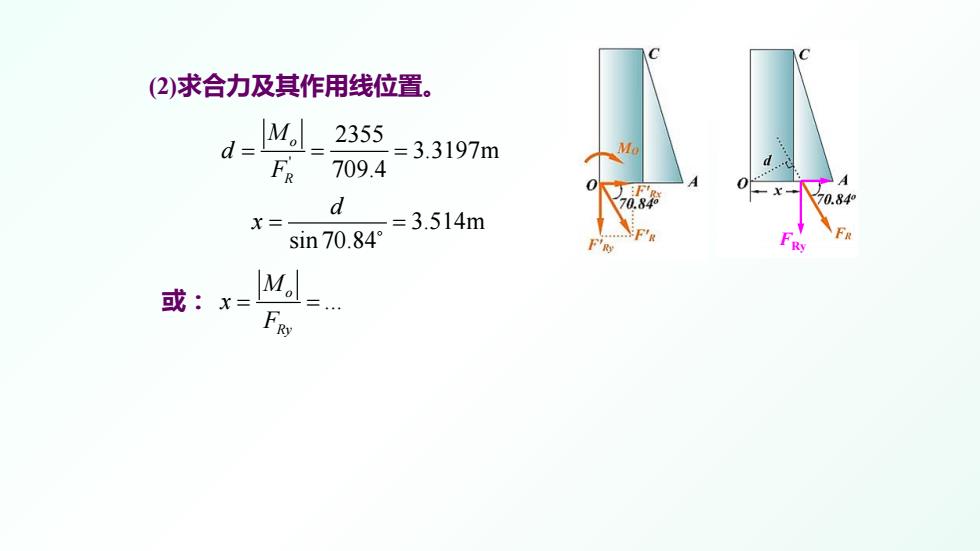
(2)求合力及其作用线位置。 M。_ 2355 d= =3.3197m FR 709.4 d 0.84 x=- =3.514m sin70.84° 或:x= M
( 2 )求合力及其作用线位置。 ' 2355 3.3197m 709.4 oR M d F = = = 3.514m sin 70.84 d x = = FRy 或: ... o Ry M x F = =
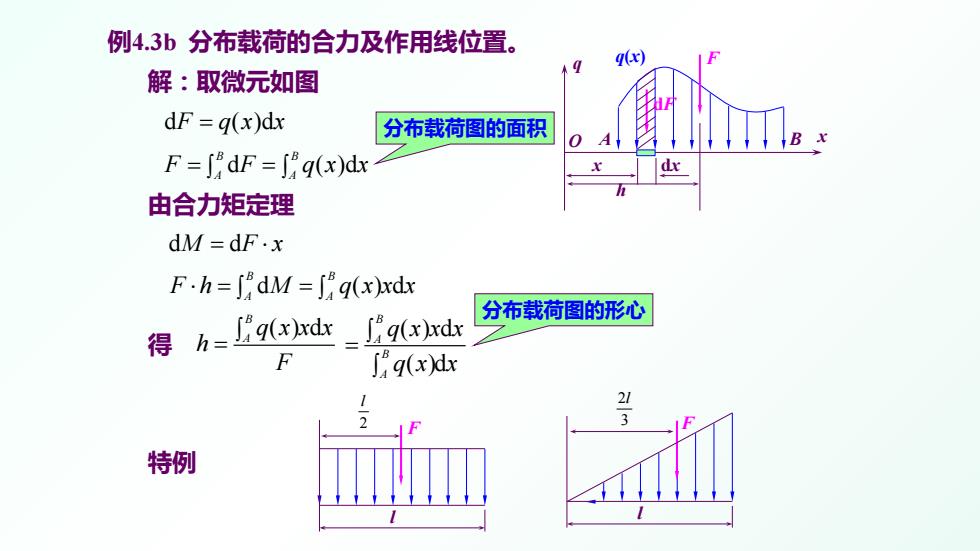
例4.3b分布载荷的合力及作用线位置。 q(x) 解:取微元如图 dF=g(x)dx 分布载荷图的面积 F=∫dF=∫q(x)dx 由合力矩定理 dM=dF.x F.h=∫dM=∫q(x)xdx 分布载荷图的形心 得 h=12q(x)xdx _∫Aqx)xdx F ∫q(xXdx 21 3 特例
由合力矩定理 得 例4.3b 分布载荷的合力及作用线位置。 解:取微元如图 d ( )d B B F F qx x A A = = ∫ ∫ d ()d B B F h M qxx x A A ⋅= = ∫ ∫ ()d B A qxx x h F ∫ = 分布载荷图的形心 分布载荷图的面积 q(x) x q F x dx h A B dF d ( )d F qx x = d d M Fx = ⋅ ()d ( )d B A B A qxx x qx x ∫ = ∫ 特例 F l 2 l F l 2 3 l O