6.5 拉伸和压缩时材料的力学性能 力学性能、机械性能:材料在外力作用下表现出的变形、破坏等方面的特性。 >选用材料,计算强度、刚度的依据 常温静载试验:常温下缓慢平稳加载。 拉伸试验机 试件:标准的尺寸和形状 标距:1 标距1 标距1 >圆截面=10d或=5d >压缩时为短圆柱,h/d-1.53
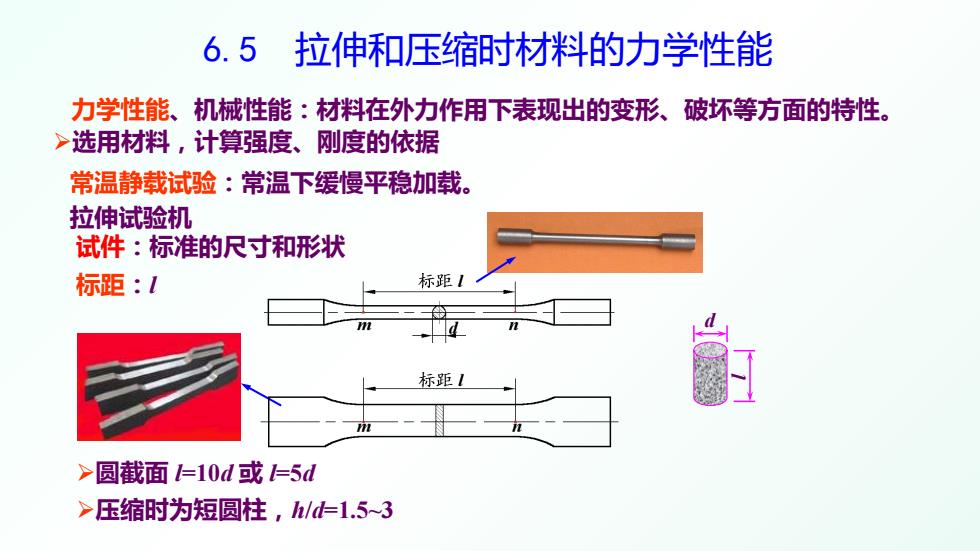
6.5 拉伸和压缩时材料的力学性能 常温静载试验:常温下缓慢平稳加载。 d l 力学性能、机械性能:材料在外力作用下表现出的变形、破坏等方面的特性。 选用材料,计算强度、刚度的依据 圆截面 l=10d 或 l=5d 压缩时为短圆柱,h/d=1.5~3 试件:标准的尺寸和形状 拉伸试验机 标距:l
低碳钢拉伸时的力学性能一塑性材料 低碳钢:含碳量在0.3%以下的碳素钢 拉伸图:F-△L曲线 AL 应力应变图:σ·曲线 >F-△L曲线与试件尺寸有关 o(MPa) 450 0筑0新0000 0.05 0.100.15 02080.25 Ep (:)低碳钢-8曲线线上特征点
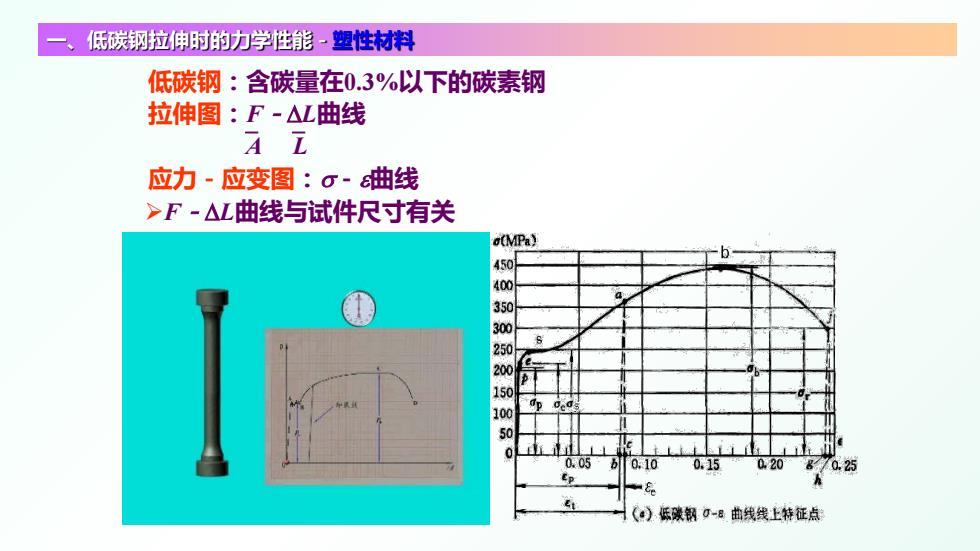
一、低碳钢拉伸时的力学性能-塑性材料 F-∆L曲线与试件尺寸有关 低碳钢:含碳量在0.3%以下的碳素钢 拉伸图:F-∆L曲线 A L 应力-应变图:σ-ε曲线
1.弹性阶段 >外力取消后,变形消失 >开始部分为直线-线弹性 9·比例极限 →195MPa O。-弹性极限 E-弹性模量 →200GPa 杨氏模量 可e Op =EE 拉压胡克定律 tana=E= 的
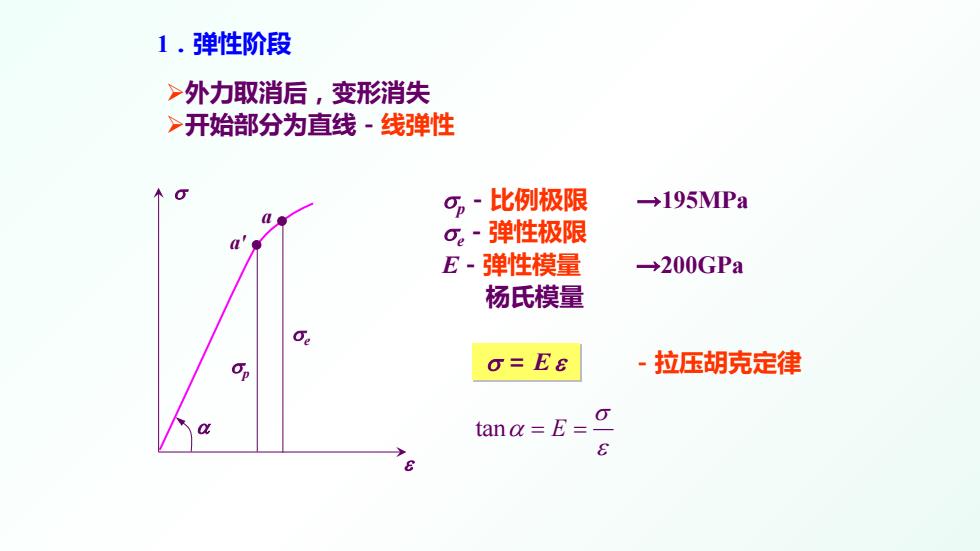
1.弹性阶段 外力取消后,变形消失 开始部分为直线-线弹性 σ ε a' σp a σe σ = E ε -拉压胡克定律 α tan E σ α ε = = σp-比例极限 →195MPa σe-弹性极限 E-弹性模量 →200GPa 杨氏模量
2.屈服(塑性流动阶段 屈服、流动:应力基本保持不变 而应变显著增加的现象。 >失去抵抗变形的能力 >显著塑性变形 >上屈服极限与试件形状、加载 速度等有关:下屈服极限较稳定 45°左右滑移线 σ,·屈服极限/流动极限 →230MPa
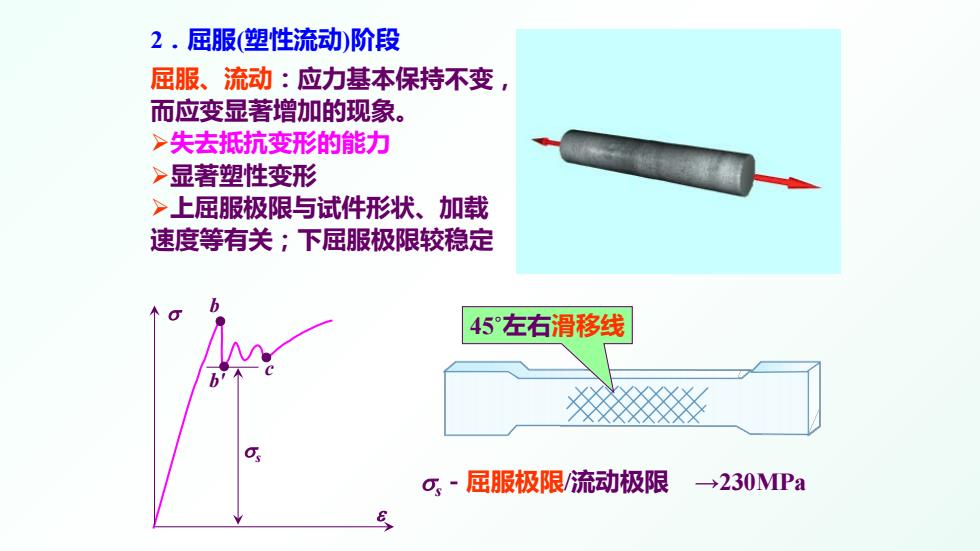
屈服、流动:应力基本保持不变, 而应变显著增加的现象。 失去抵抗变形的能力 显著塑性变形 上屈服极限与试件形状、加载 速度等有关;下屈服极限较稳定 2.屈服(塑性流动)阶段 σs-屈服极限/流动极限 →230MPa σ ε σs 45˚左右滑移线 c b b
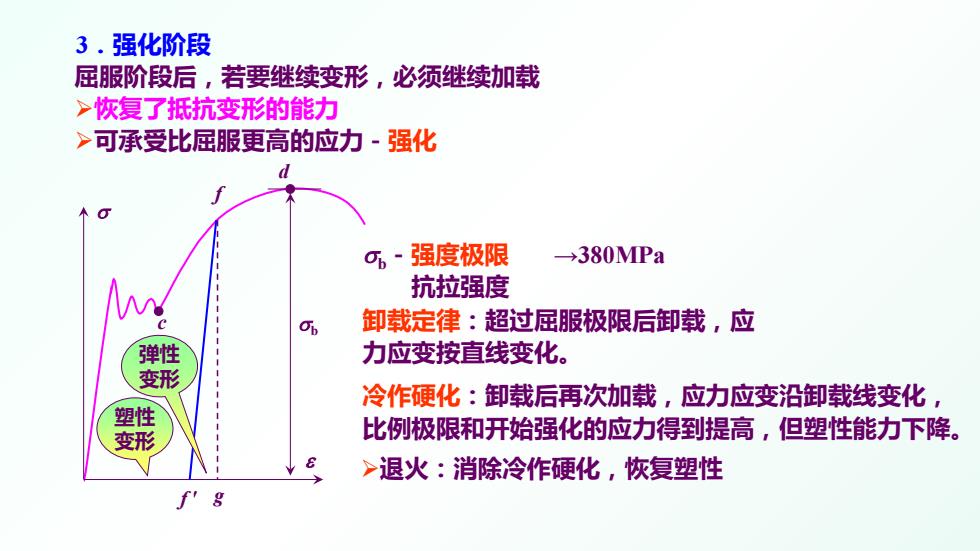
3.强化阶段 屈服阶段后,若要继续变形,必须继续加载 >恢复了抵抗变形的能力 >可承受比屈服更高的应力-强化 σ·强度极限 →380MPa 抗拉强度 卸载定律:超过屈服极限后卸载,应 弹性 力应变按直线变化。 变形 冷作硬化:卸载后再次加载,应力应变沿卸载线变化, 塑性 变形 比例极限和开始强化的应力得到提高,但塑性能力下降。 >退火:消除冷作硬化,恢复塑性 f'8
卸载定律:超过屈服极限后卸载,应 力应变按直线变化。 σb-强度极限 →380MPa 抗拉强度 冷作硬化:卸载后再次加载,应力应变沿卸载线变化, 比例极限和开始强化的应力得到提高,但塑性能力下降。 3.强化阶段 屈服阶段后,若要继续变形,必须继续加载 恢复了抵抗变形的能力 可承受比屈服更高的应力-强化 σ ε σb f f' g 弹性 变形 塑性 变形 退火:消除冷作硬化,恢复塑性 d c
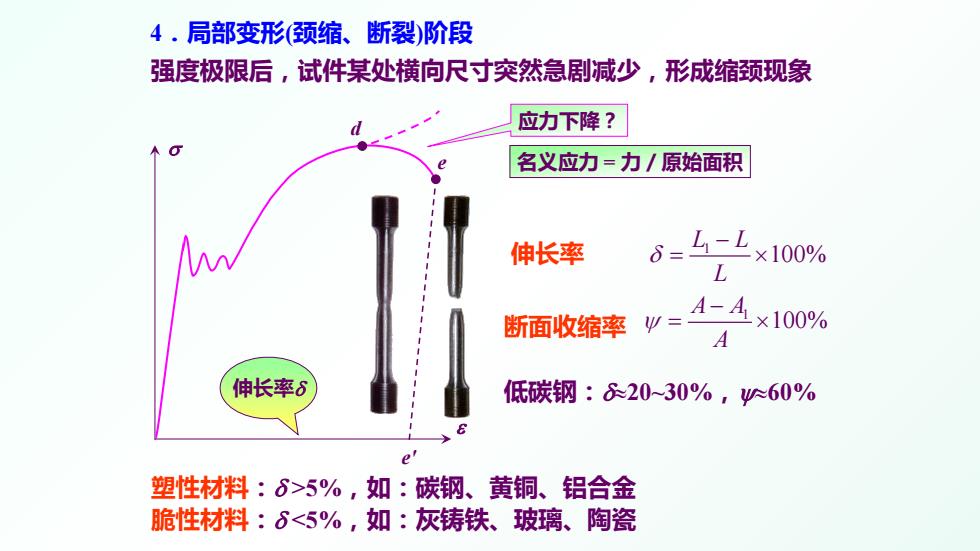
4.局部变形颈缩、断裂)阶段 强度极限后,试件某处横向尺寸突然急剧减少,形成缩颈现象 应力下降? 名义应力=力/原始面积 伸长率 6=4- ×100% 断面收缩率 W= A-A×100% A 伸长率6 低碳钢:&20~30%,y60% 塑性材料:6>5%,如:碳钢、黄铜、铝合金 脆性材料:6<5%,如:灰铸铁、玻璃、陶瓷
塑性材料:δ >5%,如:碳钢、黄铜、铝合金 脆性材料:δ <5%,如:灰铸铁、玻璃、陶瓷 伸长率 断面收缩率 4.局部变形(颈缩、断裂)阶段 σ ε 强度极限后,试件某处横向尺寸突然急剧减少,形成缩颈现象 1 100% L L L δ − = × 1 100% A A A ψ − = × 低碳钢:δ≈20~30%,ψ≈60% 应力下降? 名义应力 = 力/原始面积 e' 伸长率δ e d

二、 其他材料拉伸时的力学性能 1.无明显屈服现象的塑性材料 200r合金钢 T10A高碳钢 00.2 有的也没有 局部变形阶段 16Mh锰钢 0.2% Q235Q235钢 H62 0.2:产生0.2%塑性应变的应力 普通黄铜 作为屈服指标 -名义屈服极限 某些塑性材料的σ一£曲线 条件屈服应力
有的也没有 局部变形阶段 二、其他材料拉伸时的力学性能 σ 0.2:产生0.2%塑性应变的应力 作为屈服指标 -名义屈服极限 条件屈服应力 0.2% ε σ σ 0.2 1.无明显屈服现象的塑性材料 锰钢 普通黄铜 Q235钢 高碳钢 合金钢
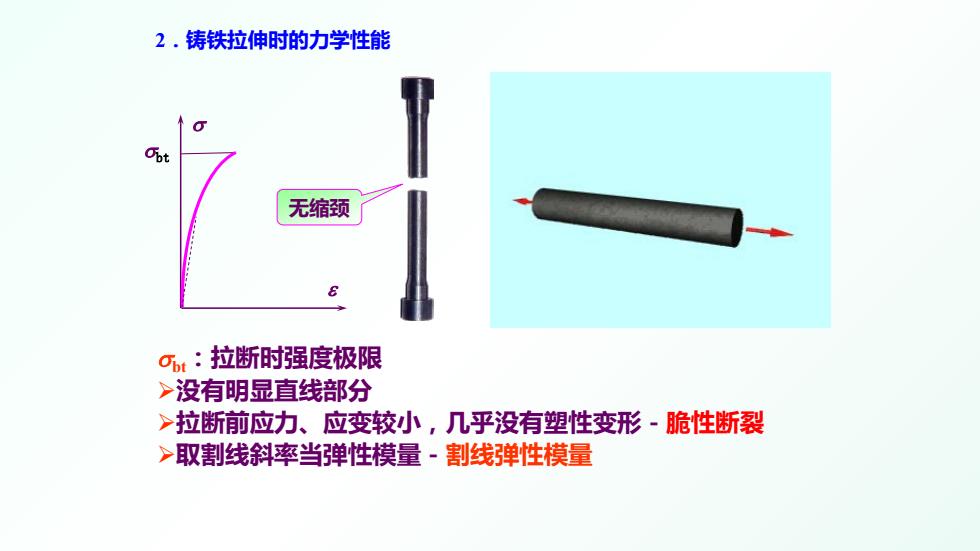
2.铸铁拉伸时的力学性能 无缩颈 Ct:拉断时强度极限 >没有明显直线部分 >拉断前应力、应变较小,几乎没有塑性变形-脆性断裂 >取割线斜率当弹性模量~割线弹性模量
σbt σbt:拉断时强度极限 没有明显直线部分 拉断前应力、应变较小,几乎没有塑性变形-脆性断裂 取割线斜率当弹性模量-割线弹性模量 σ ε 无缩颈 2.铸铁拉伸时的力学性能

弹性指标 弹性模量:E 强度指标(失效应力) 塑性材料:O、σ.2 脆性材料:O 延伸率:6 塑性指标 断面收缩率:少
强度指标(失效应力) 脆性材料:σb 塑性指标 延伸率:δ 断面收缩率:ψ 塑性材料:σs、σ0.2 弹性指标 弹性模量:E

三、材料压缩时的力学性能 低碳钢: >压缩E、σ与拉伸相当 >无压缩σ,(越压越扁) 铸铁: >C(56)ct→抗压 >45 破坏 2~5倍? 接触面摩 h】 >45°? 有的塑性 具体与铸铁 压地 擦力形成 内摩擦 材料也沿 类别有关 鼓状 减弱剪力: 斜面破坏 30m 40 裂口变尖、 300 竖直 250 Q07 004 1502河 0.25 Q0%416a12 低碳钢压缩与拉伸对比图 铸铁压缩图
低碳钢: 压缩E、σs与拉伸相当 无压缩σb(越压越扁) 铸铁: σbc≈(5~6)σbt→抗压 45~55˚破坏 有的塑性 材料也沿 斜面破坏 >45˚? 内摩擦 减弱剪力; 裂口变尖、 竖直 接触面摩 擦力形成 鼓状 2~5倍? 具体与铸铁 类别有关 三、材料压缩时的力学性能 45˚