
10.2梁的挠曲线近似微分方程及其积分 推导纯弯曲正应力时,得到: 1 M EI 上式中,惯性矩I省略了下标z 忽略剪力对变形的影响,此时M和二都是x的函数 p M(x) (x) EI
推导纯弯曲正应力时,得到: 1 M ρ EI = 1 () ( ) M x ρ x EI = ρ 忽略剪力对变形的影响,此时 M 和 都是 x 的函数 1 ρ 上式中,惯性矩 I 省略了下标 z 10.2 梁的挠曲线近似微分方程及其积分

由几何、数学知识推导可得: d2w dx2 挠曲线的微分方程: 73/2 d2w dx2 M 联立弯矩与曲率半径关系式 3/2 dw El 1M P El 小量 M 挠曲线的近似微分方程: d2w 或 Elw"M El
由几何、数学知识推导可得: 2 2 3 2 2 d 1 d d 1( ) d w x w x ρ = + 联立弯矩与曲率半径关系式 1 M ρ EI = 挠曲线的微分方程: 2 2 3 2 2 d d d 1( ) d w x M w EI x = + 小量 2 2 d d w M x EI 挠曲线的近似微分方程: = 或 EIw M ′′ =

挠曲线的近似微分方程为: d2w M d2w .=M dx2 EI dx 积分一次得转角方程: EI0=EI -jx+c 再积分一次得挠度方程: Ew=J∬(Mdx)dr+Cx+D C、D为积分常数,待定
挠曲线的近似微分方程为: 积分一次得转角方程: 再积分一次得挠度方程: 2 2 d d w M x EI = 2 2 d d w EI M x = d d d w EI EI M x C x θ = = + ∫ EIw M x x Cx D = ++ ( d )d ∫∫ C D 、 为积分常数,待定
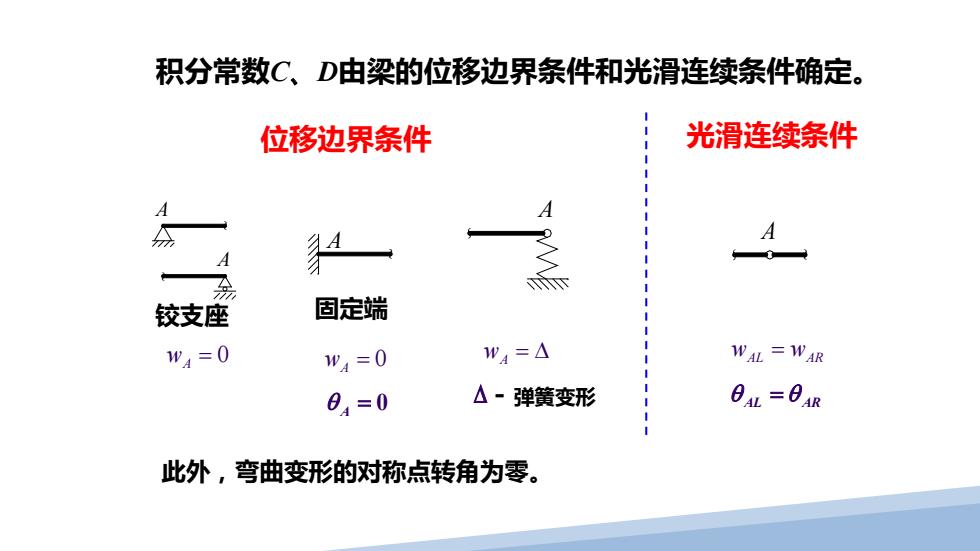
积分常数C、D由梁的位移边界条件和光滑连续条件确定。 位移边界条件 光滑连续条件 A A 分 A 铰支座 固定端 w4=0 w4=0 W4=△ WAL =WAR 04=0 △·弹簧变形 日AL=84R 此外,弯曲变形的对称点转角为零
积分常数C、D由梁的位移边界条件和光滑连续条件确定。 A A ~ ~ A ~ A ~ A 0 wA = 0 wA = = 0 θ A wA = ∆ 位移边界条件 光滑连续条件 w w AL AR = ∆-弹簧变形 θ AL = θ AR 铰支座 固定端 此外,弯曲变形的对称点转角为零

例1 求梁的转角方程和挠度方程,并求截面B处的转角和挠度,梁的EI已知。 解1)为悬臂梁,写出任意处x截面的弯矩方程 M(x)=-F(1-x)=Fx-FI 2)列挠曲线近似微分方程并积分 dw =M(x)=Fx-Fl =E16=F2-Fk+C dw 积分一次 dx 再积分一次 EhW=1Fx-1F+Cx+D 6
例1 求梁的转角方程和挠度方程,并求截面 B 处的转角和挠度,梁的 EI 已知。 解 1)为悬臂梁,写出任意处 x 截面的弯矩方程 M x F l x Fx Fl () ( ) =− − = − 2)列挠曲线近似微分方程并积分 2 2 d ( ) d w EI M x Fx Fl x = = − d 1 2 d 2 w EI EI Fx Flx C x = = −+ θ 1 1 3 2 6 2 EIw Fx Flx Cx D = − ++ 积分一次 再积分一次 θ B A B x w x l F wB

3)由位移边界条件确定积分常数 x=0,04=0 Fx2-Flx+C Lx=0, w4=0 1 -Flx2+Cx+D 6 代入求解 C=0,D=0 4)确定转角方程和挠度方程 EI CW=E10=1Fx-F dx 2 Ehw=1Fx-Flx 6 2 5)将B点坐标代入,得B处的转角和挠度 x=1时,0。= F12 F 2E7 3EI
3)由位移边界条件确定积分常数 代入求解 C D = = 0, 0 4)确定转角方程和挠度方程 5)将B点坐标代入,得B处的转角和挠度 d 1 2 d 2 w EI EI Fx Flx x = = − θ 1 1 3 2 6 2 EIw Fx Flx = − 2 3 , , 2 3 B B Fl Fl x l w EI EI = =− =− 时 θ θ B A B x w x l F wB 0, 0 A x w = = 0, 0 A x = = θ 1 2 2 EI Fx Flx C θ = −+ 1 1 3 2 6 2 EIw Fx Flx Cx D = − ++
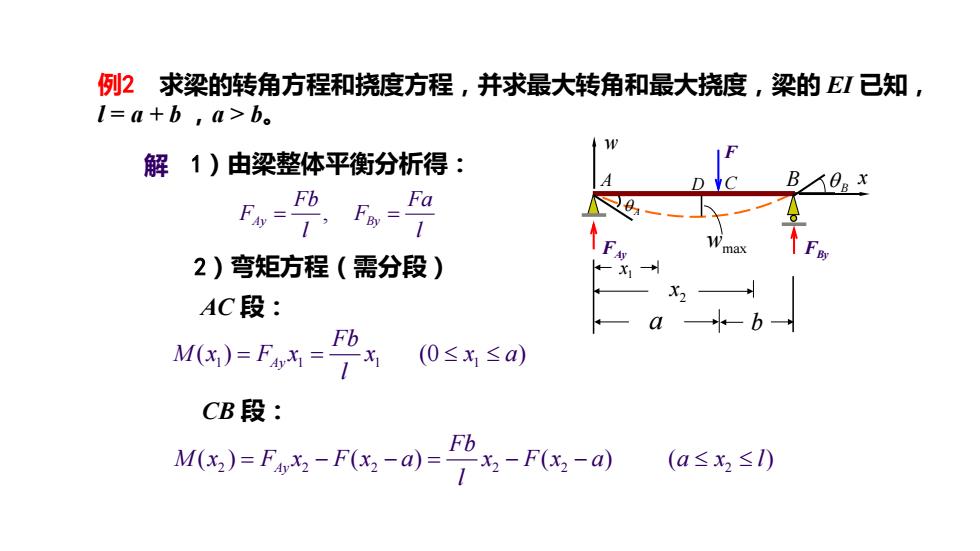
例2求梁的转角方程和挠度方程,并求最大转角和最大挠度,梁的EI已知, l=a+b,a>b。 1 解1)由梁整体平衡分析得: B人0Bx Fb Fy1 ma 2)弯矩方程(需分段) AC段: Fb M()=F= (0≤x1≤a) CB段: M,)=F5-F3,-a)= -1 x2-F(x2-a) (a≤x2≤1)
例2 求梁的转角方程和挠度方程,并求最大转角和最大挠度,梁的 EI 已知, l = a + b ,a > b。 解 1)由梁整体平衡分析得: , Ay By Fb Fa F F l l = = 2)弯矩方程(需分段) 1 11 1 ( ) (0 ) Ay Fb Mx Fx x x a l = = ≤≤ AC 段: 2 22 22 2 ( ) ( ) ( ) ( ) Ay Fb Mx F x Fx a x Fx a a x l l = − −= − − ≤≤ CB 段: wmax a b 1 x 2 x A D C F x FAy FBy θ A θ B w B
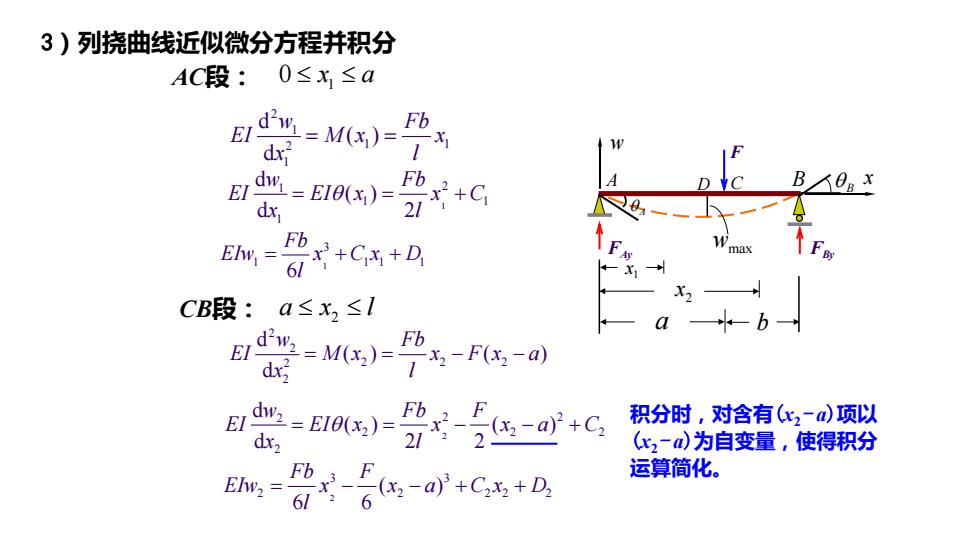
3)列挠曲线近似微分方程并积分 AC段:0≤x≤a E=M)= Fb EI dw=E10(x)= Fb dx .+Ci 21 Fb x+C+D 61 CB段:a≤x2≤1 E=M)=宁名-F6a Fb dx, dw2=E10(x2)= 2(x2-a)2+C2 积分时,对含有(x2-)项以 dx2 212 (x2一)为自变量,使得积分 运算简化。 616 (x2-a)3+C2x2+D
3)列挠曲线近似微分方程并积分 2 1 2 1 1 1 d ( ) d w Fb EI M x x x l = = 1 1 2 1 1 1 d ( ) d 2 w Fb EI EI x x C x l = = + θ 1 3 1 11 1 6 Fb EIw x C x D l = ++ 2 2 2 2 22 2 d () ( ) d w Fb EI M x x F x a x l = = −− 2 2 2 2 2 22 2 d () ( ) d 22 w Fb F EI EI x x x a C x l = = − −+ θ 2 3 3 2 2 22 2 ( ) 6 6 Fb F EIw x x a C x D l = − −+ + wmax a b 1 x 2 x A D C F x FAy FBy θ A θ B w B 积分时,对含有(x2- a)项以 (x2- a)为自变量,使得积分 运算简化。 AC段: 1 0 ≤ ≤ x a CB段: 2 ax l ≤ ≤

4)由边界条件确定积分常数 +C+D Fb 位移边界条件 61 w(0)=0 Elw2= 616 (x2-a)3+C2x2+D2 w2()=0 Fb 光滑连续条件 EI0(x)= 27+G 了=七2=a, 0(a)=82(a) EI0(x2)= 1x=x3=a, 27x-2 (x2-a)2+C w(a)=w2(a) 代入求解,得 A D B人0BX C:=C:=-1F+ 6 61 max D1=D2=0 b-
4)由边界条件确定积分常数 2 2 x l wl = = , () 0 1 1 x w = = 0, (0) 0 代入求解,得 位移边界条件 光滑连续条件 , ( ) ( ) x1 = x2 = a θ 1 a = θ 2 a 12 1 2 x x a wa wa = = = , () () l Fb C C Fbl 6 6 1 3 1 = 2 = − + D1 = D2 = 0 wmax a b 1 x 2 x A D C F x FAy FBy θ A θ B w B 1 3 1 11 1 6 Fb EIw x C x D l = ++ 2 3 3 2 2 22 2 ( ) 6 6 Fb F EIw x x a C x D l = − −+ + 1 2 1 1 ( ) 2 Fb EI x x C l θ = + 2 2 2 2 22 () ( ) 2 2 Fb F EI x x x a C l θ = − −+

5)确定转角方程和挠度方程 AC段:0≤x1≤a w EI0,= Fb2_Fb(P-B) -X 21161 Elw Fb-Fb心-b)x 61161 CB段:a≤x2≤I EI02= X2一 5,-a--6) 21 61 EIw2= 61 6 61
5)确定转角方程和挠度方程 ( ) 2 6 2 2 2 1 1 l b l Fb x l Fb EIθ = − − 1 3 22 1 1 ( ) 6 6 Fb Fb EIw x l b x l l =− − ( ) 6 ( ) 2 2 2 2 2 2 2 2 2 l b l Fb x a F x l Fb EIθ = − − − − 3 3 22 2 22 2 () ( ) 66 6 Fb F Fb EIw x x a l b x l l = − −− − wmax a b 1 x 2 x A D C F x FAy FBy θ A θ B w B AC段: 1 0 ≤ ≤ x a CB段: 2 ax l ≤ ≤