
目录 CONTENTS 欧拉公式的另外一种形式 12 欧拉公式的适用范围 经验公式 压杆分类
1 2 3 欧拉公式的另外一种形式 欧拉公式的适用范围 经验公式 目录 CONTENTS 4 压杆分类

1、欧拉公式的另外一种形式 π2E1 临界压力:F。= 一柔度(长细比) (l)2 临界应力: π2E1 0=1 A (ul)A 柔度是压杆稳定问题中的一个重要参数,它全 面反映了压杆长度、约束条件、截面尺寸和形 状对临界应力的影响。 惯性矩: I=iA 广一惯性半径 π2Ei2A π2E π2E er 欧拉公式的另一种形式 (uD2A 3
1、欧拉公式的另外一种形式 临界压力: 临界应力: 惯性矩: i 惯性半径 cr cr F A σ = 2 2 ( ) EI l A π µ = 2 I iA = 2 cr 2 E l i π σ µ = 2 2 π E λ = —欧拉公式的另一种形式 —柔度 (长细比) 柔度 是压杆稳定问题中的一个重要参数,它全 面反映了压杆长度、约束条件、截面尺寸和形 状对临界应力的影响

2、欧拉公式的使用范围 材料和直 问题 :径均相同 (1)能不能应用欧拉公式计算这里的四根 压杆的临界载荷? (2)这里的四根杆是不是都会发生失稳? 分析:(1)欧拉公式的推导使用了挠曲线近似微分方程 (2)挠曲线近似微分方程使用条件为:材料服从胡克定律、小变形 结论: 应力不超过比例极限 Ocr≤p π2E π2E 元2 0 π2E 1≥2 入1只与材料的性质有关 OP
2、欧拉公式的使用范围 问题: (1)能不能应用欧拉公式计算这里的四根 压杆的临界载荷? (2)这里的四根杆是不是都会发生失稳? 结论: 应力不超过比例极限 σ cr ≤ σ p (1)欧拉公式的推导使用了挠曲线近似微分方程 (2)挠曲线近似微分方程使用条件为:材料服从胡克定律、小变形 分析: 2 2 cr λ π σ E = σ p ≤ P 2 σ π λ E ≥ P 2 1 σ π λ E = λ ≥ λ1 λ1只与材料的性质有关

3、经验公式 若入<九 ,,则临界应Oc大于比例极限Op,欧拉公式不再适用; 当ocr=c时,发生强度破坏;处于中间的部分,σs≤o≤op时进行直线修正,使 用直线经验公式。 直线公式的最小柔度 a-os 经验公式:直线型 =a-b入 b 其中a、b是与材料性质有关的常数,可查表。 直线经验公式的适用范围入,≤入≤几 用直线经验公式时,O,≤0≤0 当入≤22时,就发生强度失效,而不是失稳。 元2≤九≤几1 A
3、 经验公式 若 ,则临界应 大于比例极限 ,欧拉公式不再适用; 当σcr =σs时,发生强度破坏;处于中间的部分,σS≤σcr≤σP时进行直线修正,使 用直线经验公式。 p σ cr σ p λ λ < 经验公式: 直线型 其中a、b是与材料性质有关的常数,可查表。 2 a s b σ λ − 直线公式的最小柔度 = 直线经验公式的适用范围 用直线经验公式时, λ 2 ≤ λ ≤ λ1 当 λ ≤ λ2 时,就发生强度失效,而不是失稳。 A F σ cr = σσσ p s ≤ ≤ cr λ 2 ≤ λ ≤ λ1
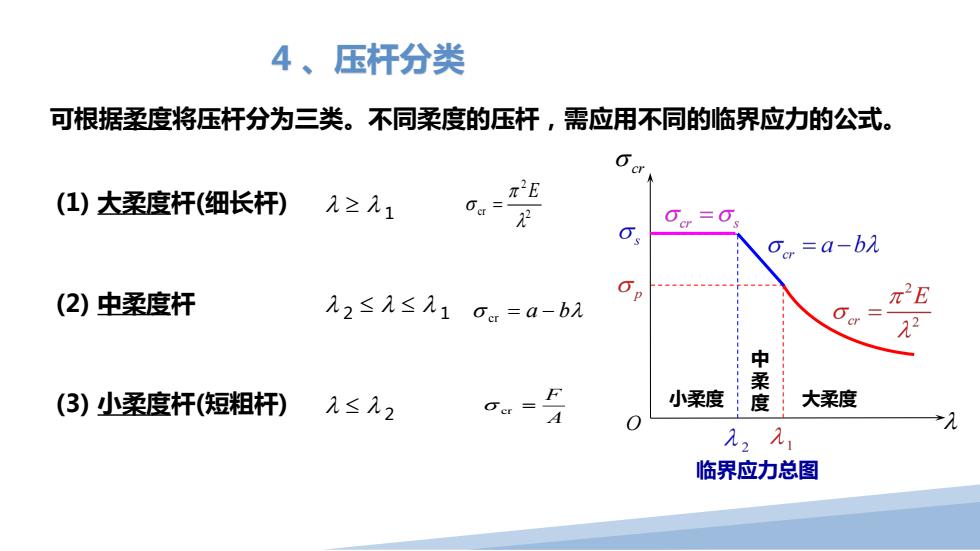
4、压杆分类 可根据柔度将压杆分为三类。不同柔度的压杆,需应用不同的临界应力的公式。 (1)大柔度杆(细长杆) 12九1 π2E Oa= Oor=a-bA (2)中柔度杆 2≤元≤九1o=a-bM π2E 中 (3)小柔度杆(短粗杆) 元≤12 小柔度 度 大柔度 临界应力总图
4 、压杆分类 可根据柔度将压杆分为三类。不同柔度的压杆,需应用不同的临界应力的公式。 (1) 大柔度杆(细长杆) λ ≥ λ 1 (2) 中柔度杆 λ 2 ≤ λ ≤ λ 1 (3) 小柔度杆(短粗杆) λ ≤ λ 2 O λ σ cr 小柔度 中 柔 度 大柔度 2 2 cr λ π σ E = σ cr = a − bλ A F σ cr = 临界应力总图