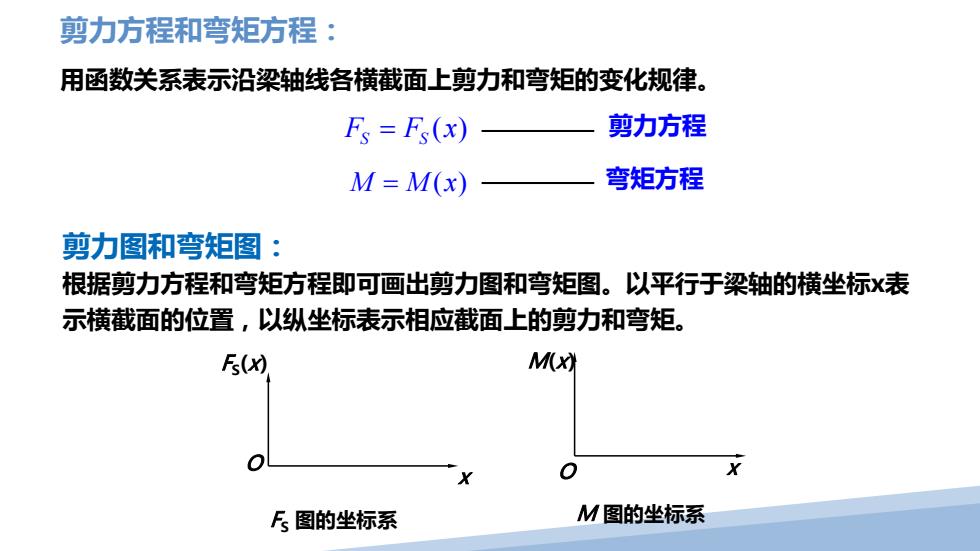
剪力方程和弯矩方程: 用函数关系表示沿梁轴线各横截面上剪力和弯矩的变化规律。 Fs =Fs(x) 剪力方程 M=M(x) 弯矩方程 剪力图和弯矩图: 根据剪力方程和弯矩方程即可画出剪力图和弯矩图。以平行于梁轴的横坐标x表 示横截面的位置,以纵坐标表示相应截面上的剪力和弯矩。 Fs(x) M(x) X F图的坐标系 M图的坐标系
剪力图和弯矩图: 根据剪力方程和弯矩方程即可画出剪力图和弯矩图。以平行于梁轴的横坐标x表 示横截面的位置,以纵坐标表示相应截面上的剪力和弯矩。 用函数关系表示沿梁轴线各横截面上剪力和弯矩的变化规律。 剪力方程和弯矩方程: ( ) F Fx S S = M Mx = ( ) 剪力方程 弯矩方程 x F S(x) F S 图的坐标系 O M 图的坐标系 O x M(x)
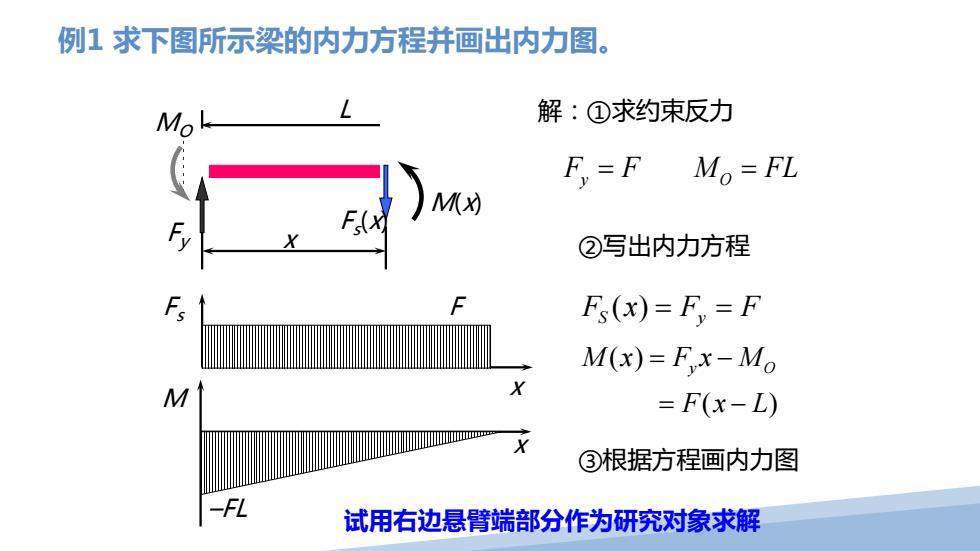
例1求下图所示梁的内力方程并画出内力图。 Mo 解:①求约束反力 F=F Mo=FL M ②写出内力方程 Fs(x)=F,=F M(x)=F,x-Mo M X =F(x-D) ③根据方程画内力图 -FL 试用右边悬臂端部分作为研究对象求解
例1 求下图所示梁的内力方程并画出内力图。 ( ) Fx F F S y = = 解:①求约束反力 ( ) () M x Fx M y O Fx L = − = − ②写出内力方程 F F M FL y O = = F Fy L ③根据方程画内力图 M(x) x Fs (x) Fs M x x F –FL MO 试用右边悬臂端部分作为研究对象求解
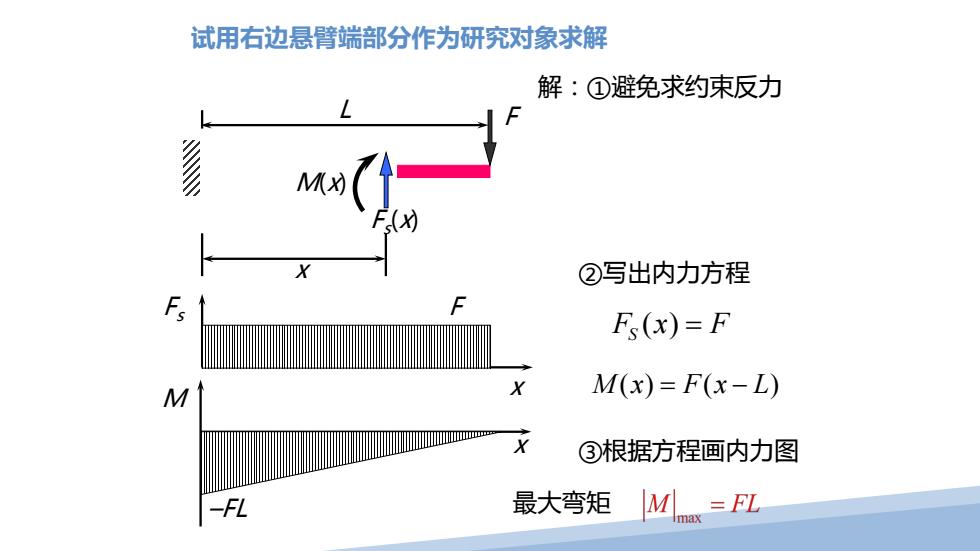
试用右边悬臂端部分作为研究对象求解 解:①避免求约束反力 Mx ②写出内力方程 F(x)=F M M(x)=F(x-L) ③根据方程画内力图 -FL 最大弯矩 M=FL
( ) Fx F S = Mx Fx L () ( ) = − ②写出内力方程 F L ③根据方程画内力图 Fs M x x F –FL 试用右边悬臂端部分作为研究对象求解 解:①避免求约束反力 M(x) x Fs (x) 最大弯矩

M 危险截面 -FL 最大弯矩 M=FL Imax
M x –FL 最大弯矩 危险截面

例2悬臂梁受均布载荷作用 试写出剪力和弯矩方程,并画出剪力图和 弯矩图。 M(x) 解:任选一截面X,写出剪力和弯矩方程 F(x)=qx (0≤x<) Fs Fs(x) gl M(x)=gr2/2(0≤x<) 依方程画出剪力图和弯矩图 g212 M 由剪力图、弯矩图可见。最大剪力和弯矩分 g12/8 别为 IFsles =ql WMle =gr 12
q 例2 悬臂梁受均布载荷作用 试写出剪力和弯矩方程,并画出剪力图和 弯矩图。 解:任选一截面x,写出剪力和弯矩方程 x ( ) (0 ) F x qx x l S = ≤< 2 M x qx x l ( ) / 2 (0 ) = ≤< 依方程画出剪力图和弯矩图 FS x M x l 由剪力图、弯矩图可见。最大剪力和弯矩分 别为 q x ( ) F x S
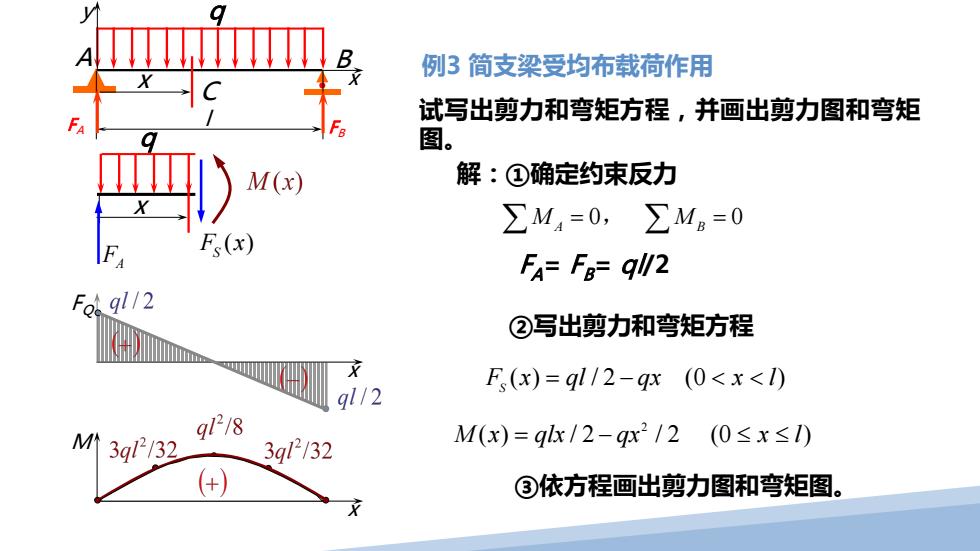
例3简支梁受均布载荷作用 试写出剪力和弯矩方程,并画出剪力图和弯矩 图。 M(x) 解:①确定约束反力 ∑M4=0,∑MB=0 Fs(x) FA=Fa=ql/2 Fot ql/2 ②写出剪力和弯矩方程 F(x)=gl/2-gx (0<x<1) gl/2 M作 3gl/32 3gl2132 M(x)=gl/2-qx2/2(0≤x≤) ③依方程画出剪力图和弯矩图
A B F l A q FB 例3 简支梁受均布载荷作用 试写出剪力和弯矩方程,并画出剪力图和弯矩 图。 解:①确定约束反力 0 0 ∑ ∑ M M A B = , = FA= F B= ql/2 ②写出剪力和弯矩方程 y x C x ③依方程画出剪力图和弯矩图。 FQ x M x ( ) / 2 (0 ) F x ql qx x l S = − << 2 M x qlx qx x l ( ) / 2 / 2 (0 ) = − ≤≤ q x ( ) F x S FA
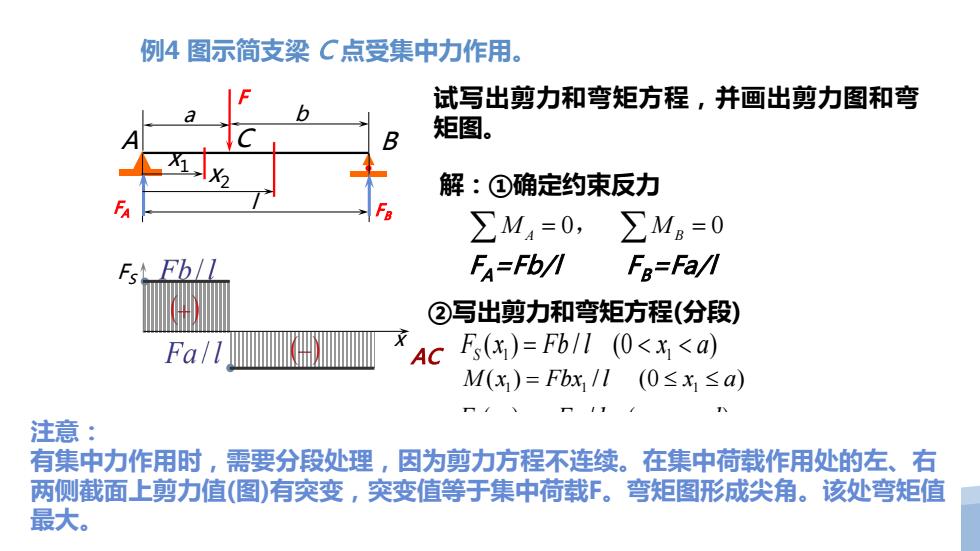
例4图示简支梁C点受集中力作用。 试写出剪力和弯矩方程,并画出剪力图和弯 矩图。 解:①确定约束反力 ∑M4=0,∑Mg=0 Est Fb/l FA=Fb/l Fa=Fa/I ②写出剪力和弯矩方程(分段) Fa/l AC Fs(x)=Fb/l (0<x<a) M(x)=Fbx/1(0≤x,≤a) n/ n II 注意: 有集中力作用时,需要分段处理,因为剪力方程不连续。在集中荷载作用处的左、右 两侧截面上剪力值(图)有突变,突变值等于集中荷载F。弯矩图形成尖角。该处弯矩值 最大
A B F l A FB 例4 图示简支梁 C 点受集中力作用。 试写出剪力和弯矩方程,并画出剪力图和弯 矩图。 解:①确定约束反力 0 0 ∑ ∑ M M A B = , = FA=Fb/l F B=Fa/l ②写出剪力和弯矩方程(分段) x2 FS x M x x1 AC 1 1 ( ) / (0 ) F x Fb l x a S = << 11 1 M x Fbx l x a ( ) / (0 ) = ≤≤ CB 2 2 () / ( ) F x Fa l a x l S =− < < 22 2 M x Fa l x l a x l ( ( )/ ( ) )= − ≤≤ ③依方程画出剪力图和弯矩图。 C F a b 注意: 有集中力作用时,需要分段处理,因为剪力方程不连续。在集中荷载作用处的左、右 两侧截面上剪力值(图)有突变,突变值等于集中荷载F。弯矩图形成尖角。该处弯矩值 最大
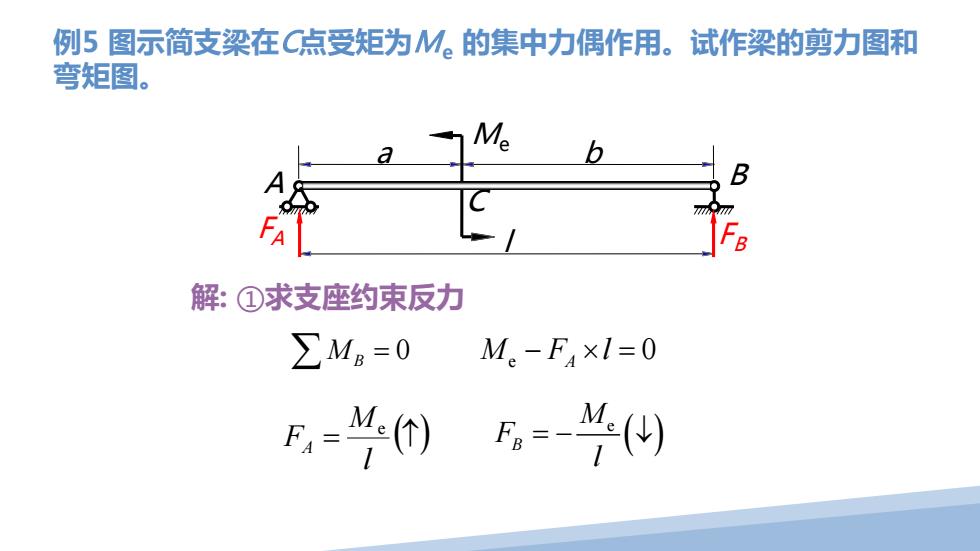
例5图示简支梁在C点受矩为M。的集中力偶作用。试作梁的剪力图和 弯矩图。 Me 解:①求支座约束反力 ∑MB=0 M。-F4×1=0 =
例5 图示简支梁在C点受矩为Me 的集中力偶作用。试作梁的剪力图和 弯矩图。 解: ①求支座约束反力 = (↑) l M FA e ( ) e B M F l =− ↓ 0 ∑ MB = 0 Me − FA ×l = Me B l A C a b FB FA
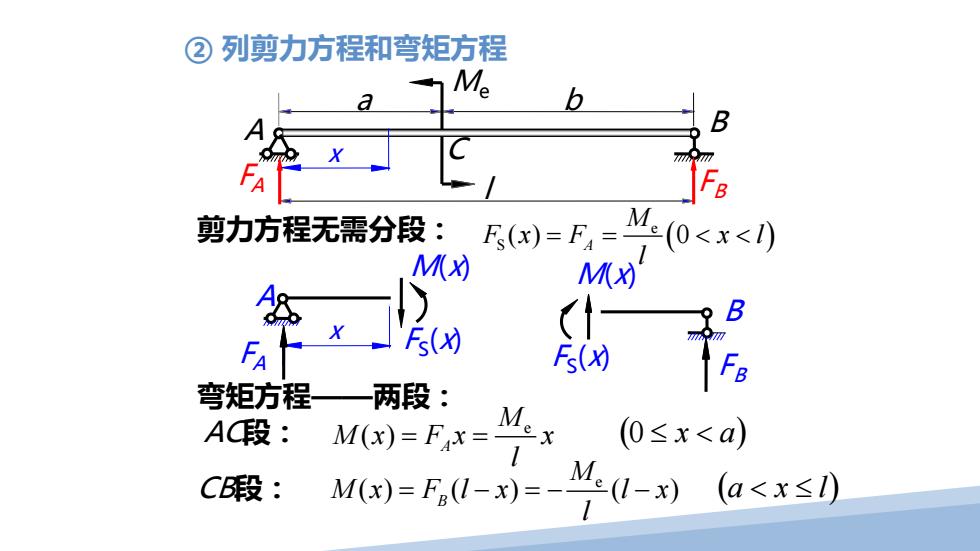
②列剪力方程和弯矩方程 Me 剪力方程无需分段:1 M(X) M(x) B Fs(x) Fa 弯矩方程—两段: AC段:M(x)=F4x= 0≤x<a C段: M0)=r0-=-41-) (a<x≤l
Me B l A C a b FB FA ② 列剪力方程和弯矩方程 剪力方程无需分段: ( ) e S () 0 A M Fx F x l l = = << 弯矩方程——两段: AC段: CB段: e ( ) A M M x Fx x l = = e () ( ) ( ) B M Mx F l x l x l = − =− − (a < x ≤ l) (0 ≤ x < a) x A FA M(x) FS(x) x FB B FS(x) M(x)
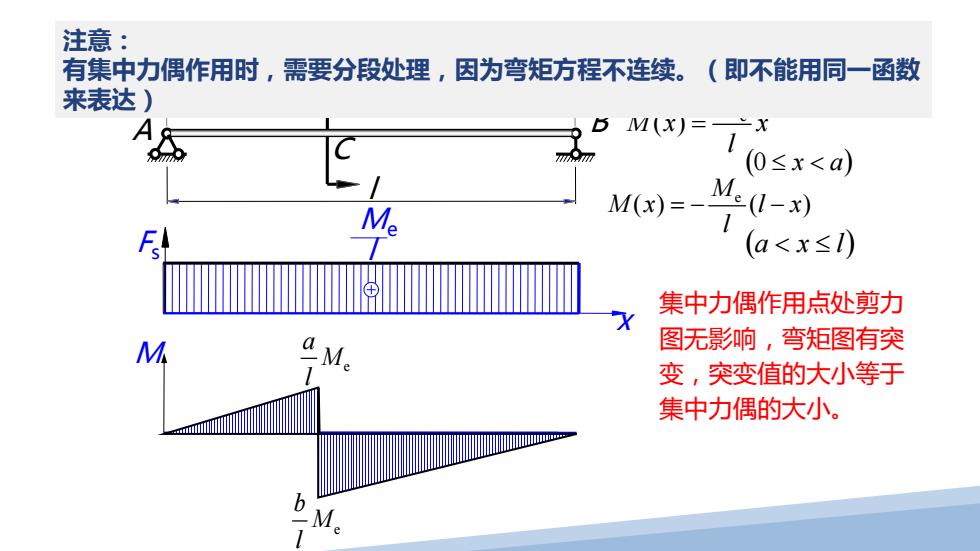
注意: 有集中力偶作用时,需要分段处理,因为弯矩方程不连续。(即不能用同一函数 来表达) M(x)=÷x (0≤x<a) Me M(x)=- Ml-x刈 (a<x≤l) 集中力偶作用点处剪力 M M 图无影响,弯矩图有突 变,突变值的大小等于 集中力偶的大小
③作剪力图和弯矩图 e S ( ) M F x l = Fs l x Me 集中力偶作用点处剪力 图无影响,弯矩图有突 变,突变值的大小等于 集中力偶的大小。 B l A C a b e ( ) M Mx x l = e () ( ) M Mx l x l =− − (a < x ≤ l) (0 ≤ x < a) M e b M l e a M l Me 注意: 有集中力偶作用时,需要分段处理,因为弯矩方程不连续。(即不能用同一函数 来表达)