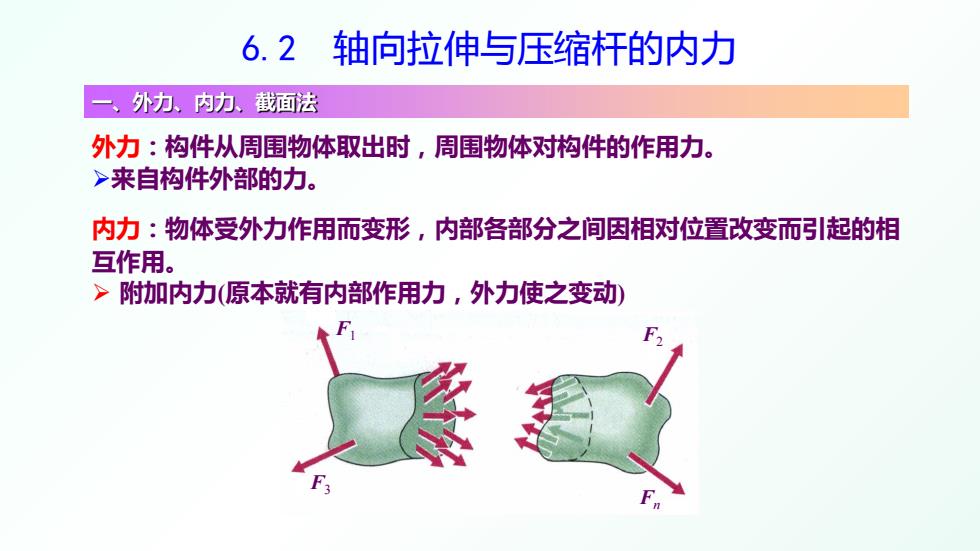
6.2 轴向拉伸与压缩杆的内力 一、外力、内力、截面法 外力:构件从周围物体取出时,周围物体对构件的作用力。 >来自构件外部的力。 内力:物体受外力作用而变形,内部各部分之间因相对位置改变而引起的相 互作用。 >附加内力(原本就有内部作用力,外力使之变动)
6.2 轴向拉伸与压缩杆的内力 一、外力、内力、截面法 外力:构件从周围物体取出时,周围物体对构件的作用力。 来自构件外部的力。 内力:物体受外力作用而变形,内部各部分之间因相对位置改变而引起的相 互作用。 附加内力(原本就有内部作用力,外力使之变动) F2 F1 Fn F3
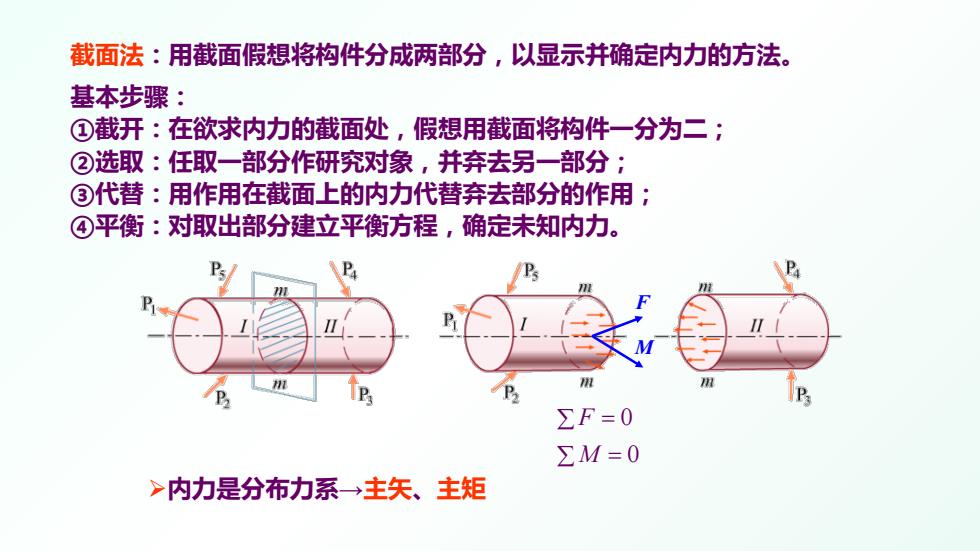
截面法:用截面假想将构件分成两部分,以显示并确定内力的方法。 基本步骤: ①截开:在欲求内力的截面处,假想用截面将构件一分为二; ②选取:任取一部分作研究对象,并弃去另一部分; ③代替:用作用在截面上的内力代替弃去部分的作用; ④平衡:对取出部分建立平衡方程,确定未知内力。 ∑F=0 ∑M=0 >内力是分布力系主矢、主矩
截面法:用截面假想将构件分成两部分,以显示并确定内力的方法。 基本步骤: ①截开:在欲求内力的截面处,假想用截面将构件一分为二; ②选取:任取一部分作研究对象,并弃去另一部分; ③代替:用作用在截面上的内力代替弃去部分的作用; ④平衡:对取出部分建立平衡方程,确定未知内力。 内力是分布力系→主矢、主矩 F M 0 0 F M ∑ = ∑ =
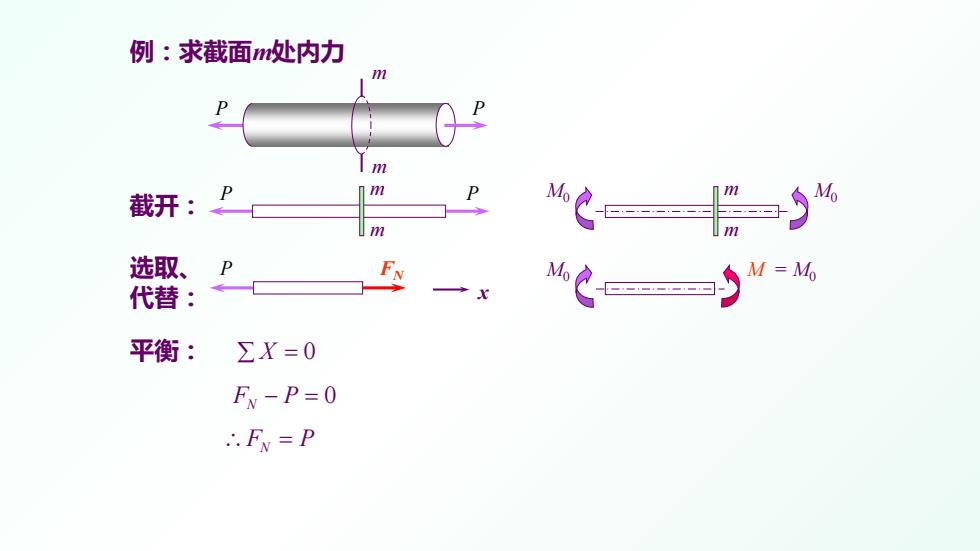
例:求截面处内力 m 截开: m 选取、 M Mo 代替: 平衡: ∑X=0 FN-P=0 ∴FN=P
例:求截面m处内力 ∑ X = 0 0 F P N − = ∴ = F P N 截开: 选取、 代替: 平衡: P P P FN m m x m P P m M0 M M0 m M0 m = M0

二 轴力、轴力图 轴力:拉压时截面内力的合力,与轴线重合 (a) >拉伸时为正(与外法线同向) >压缩时为负(与外法线反向) (b) FN R (c) F>0 轴力图:轴力沿轴线变化图 >可确定最大轴力及其截面(危险截面)位置, F<0 为强度计算提供依据
FN>0 FN FN FN<0 FN FN 二、轴力、轴力图 R 轴力:拉压时截面内力的合力,与轴线重合 拉伸时为正(与外法线同向) 压缩时为负(与外法线反向) 轴力图:轴力沿轴线变化图 可确定最大轴力及其截面(危险截面)位置, 为强度计算提供依据

例杆A、B、C、D作用力分别为5P、8P、4P、P,方向如图,试画出杆的轴力图。 B D 解:()求OA段内力FN1:设置截 面如图 P.=5P PR=8P PO=4P PD=P ∑F.=0 B -FNI+P-PB+Pc+PD=0 5P 8P 4P -F1+5P-8P+4P+P=0 轴力按 B .F1=2P 正向假设 8P 4P (2)同理求得AB、BC、CD段内力: FN2=-3P、FN3=5P、FN4=P (3)轴力图如下: ↑FN 5 2P 安MX 3P
例 杆A、B、C、D作用力分别为5P、8P、4P、P,方向如图,试画出杆的轴力图。 解: (1)求OA段内力FN1:设置截 面如图 0 ∑ F x = N1 0 − +−++ = F PPPP ABCD N1 − + − + += F P P PP 5 8 4 0 N1 ∴ = F P2 A B C D PA=5P PB=8P PC=4P PD=P O A B C D 5P 8P 4P P FN1 FN2 B C D 8P 4P P C D 4P P FN3 D P FN4 (2)同理求得AB、BC、CD段内力: FN2= –3P、FN3= 5P、FN4= P (3)轴力图如下: 轴力按 正向假设 FN x 2P 3P 5P P + − + +

例图示铅垂杆长L=10m,横截面积A=0.1m2,材料密度p7.96×103kg/m3,受自 重作用。试作轴力图。 解:取x坐标向上,原点在底端中点。 F(x) 距底端x处设置截面,取下段分析: ∑F=0 Fv(x)-pgAx=0 ∴.F(x)=PgAx 最大轴力在顶面: F=P8AL =7.96×103×9.8×0.1×10N =78×103N =78kN
解:取x 坐标向上,原点在底端中点。 距底端x处设置截面,取下段分析: 例 图示铅垂杆长L=10m,横截面积A=0.1m2,材料密度ρ=7.96×103 kg/m3,受自 重作用。试作轴力图。 FN x O 0 L ∑ F x = F x gAx N () 0 − = ρ N ∴ = F x gAx ( ) ρ Nmax 3 3 7.96 10 9.8 0.1 10 N 78 10 N =78 kN = ρ = ×××× = × F gAL FN(x) x 最大轴力在顶面: