
目录 CONTENTS A-1 静矩和形心 A-2惯性矩、惯性积和惯性半径 A-3平行移轴公式组合图形的惯性矩计算
目录 CONTENTS A–1 静矩和形心 A–2 惯性矩、惯性积和惯性半径 A–3 平行移轴公式 组合图形的惯性矩计算
A-3平行移轴公式 yc和是通过形心的坐标轴(即,C是形心) l,=Jz2d4=∫(+a2d4 -Lcd afed a-A yc ☑ ∫dM=Aze=0 为图形对转心轴的随4值应等于零 I:=I+b2A 间一平面内对所有相互平行的坐标轴的 惯性矩,对形心轴的最小。 I=lye-+abA
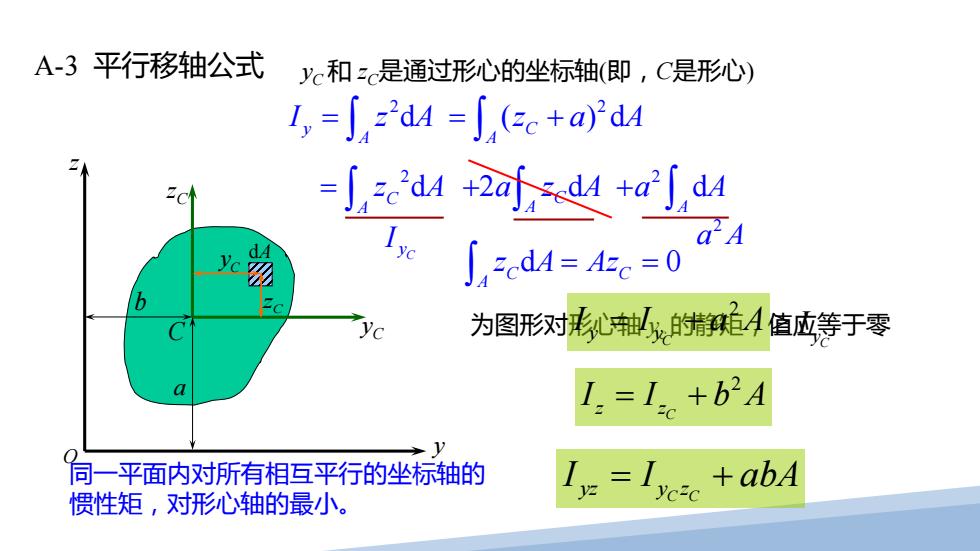
C yC zC 同一平面内对所有相互平行的坐标轴的 惯性矩,对形心轴的最小。 为图形对形心轴 yc 的静矩,值应等于零 2 C y y I I aA = + C C yz y z I I abA = + A-3 平行移轴公式 b a dA 2 d y A I zA = ∫ 2 ( )d C A = + z aA ∫ 2 d C A = z A ∫ 2 dC A + azA ∫ 2 d A +a A ∫ Cy I 2 a A d 0 C C A z A Az = = ∫ 2 C z z I I bA = + yC 和 zC是通过形心的坐标轴(即,C是形心) z y O Cy ≥ I Cz Cy
思考: y 已知平面图形面积为A,y轴过形心,yC 1、y2三轴平行。若图形对y轴的惯性 b -yc 矩为I,则 2I3卡1+(a+b)2A吗? 注意:y1、y2均不是形心轴 实际上,1为=1+b2·A I=1+a2.A 得1=1-a2,A+b2A
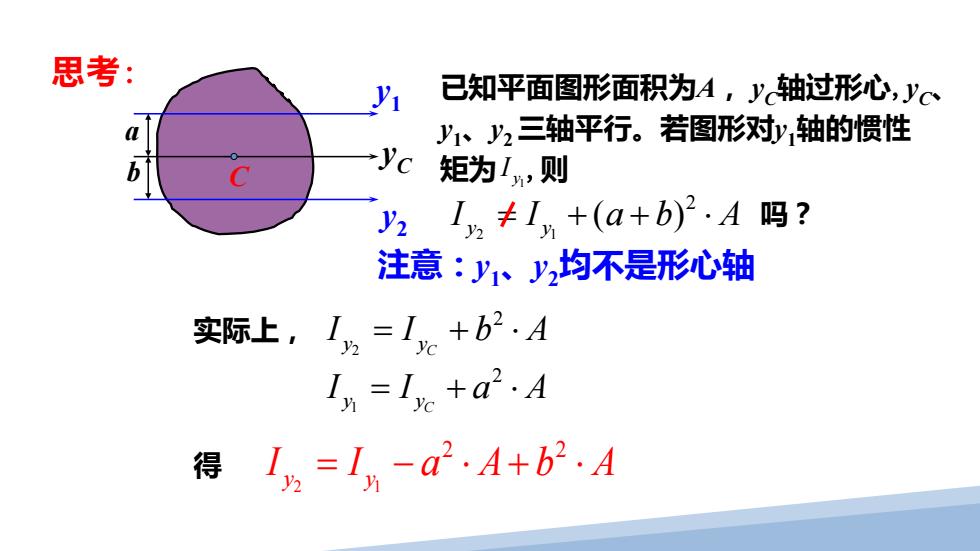
思考: C yC y2 y1 a b 已知平面图形面积为A, yC轴过形心,yC、 y1、y2 三轴平行。若图形对y1轴的惯性 矩为 I y1 ,则 2 1 2 ( ) y y I I ab A = ++ ⋅ 吗? 注意:y1、y2均不是形心轴 2 1 2 2 y y I I a Ab A = − ⋅+ ⋅ 实际上, 2 2 C y y I I bA = +⋅ 1 2 C y y I I aA = +⋅ 得