
目录 CONTENTS A-1 静矩和形心 A-2 惯性矩、惯性积和惯性半径 A-3平行移轴公式组合图形的惯性矩计算
目录 CONTENTS A–1 静矩和形心 A–2 惯性矩、惯性积和惯性半径 A–3 平行移轴公式 组合图形的惯性矩计算

A-2惯性矩、惯性积、极惯性矩、惯性半径 一、惯性矩: 绕轴 是面积与它到轴的距离的平方之积(二次矩)。 衡量一个物体抵抗转动的能力 1,=d4 恒为正值 2 1.=∫ydM 二、极惯性矩: 绕点是面积对极点的二次矩。 0 Ln=∫4pd4=∫0y2+2)dA=J4yd4+d1=L.+1
2 2 d d y A z A I zA I yA = = ∫ ∫ 二、极惯性矩: 是面积对极点的二次矩。 2 22 2 2 d ( )d d d p z y A A AA I A y z A yA zA I I = = + = + =+ ρ ∫ ∫ ∫∫ 一、惯性矩: 是面积与它到轴的距离的平方之积(二次矩)。 A-2 惯性矩、惯性积、极惯性矩、惯性半径 恒为正值 衡量一个物体抵抗转动的能力 dA y z z y ρ O 绕轴 绕点
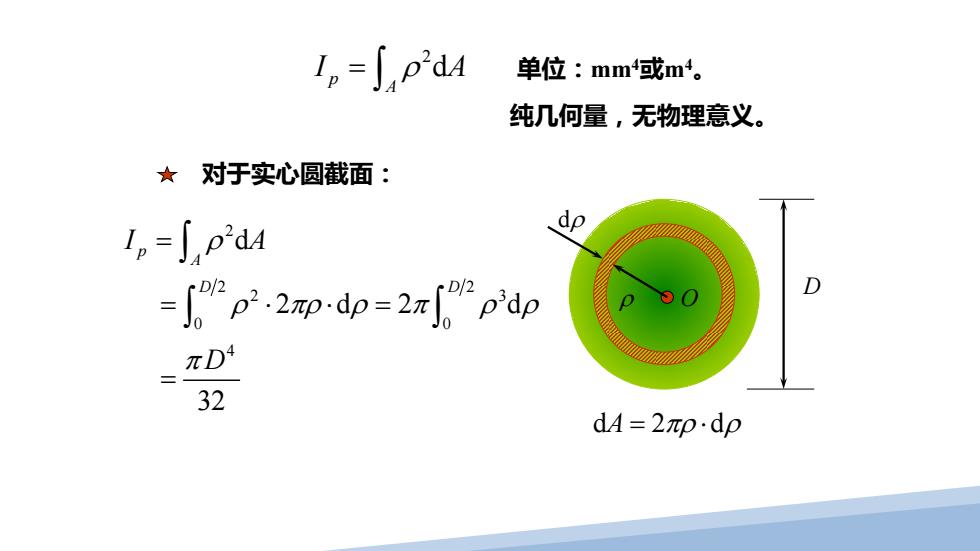
1。=jp2d1 单位:mm或m4。 纯几何量,无物理意义。 ☆对于实心圆截面: 1。=∫p2dA dp -p2xpdp=2xp'dp 32 dA=2p·dp
单位:mm4或m4 。 2 d p A I A = ρ ∫ 对于实心圆截面: D ρ dρ O 纯几何量,无物理意义。 d2d A = ⋅ πρ ρ 2 2 2 2 3 0 0 4 d 2d2 d 32 p A D D I A D ρ ρ πρ ρ π ρ ρ π = = ⋅ ⋅= = ∫ ∫ ∫

☆对于空心圆截面: dp 1n=∫p2d1 =p22w-d0 32D-d dA=2np.dp (1-a4) 32 a=哥 惯性矩、极惯性矩的计算具有可加性。/,= D4 πd4 32 32
对于空心圆截面: 2 2 2 2 4 4 4 4 d 2d () 32 (1 ) 32 p A D d I A D d D ρ ρ πρ ρ π π α = = ⋅⋅ = − = − ∫ ∫ ( ) D d α = 惯性矩、极惯性矩的计算具有可加性。 d D O ρ dρ 4 4 32 32 p D d I π π = − d2d A = ⋅ πρ ρ
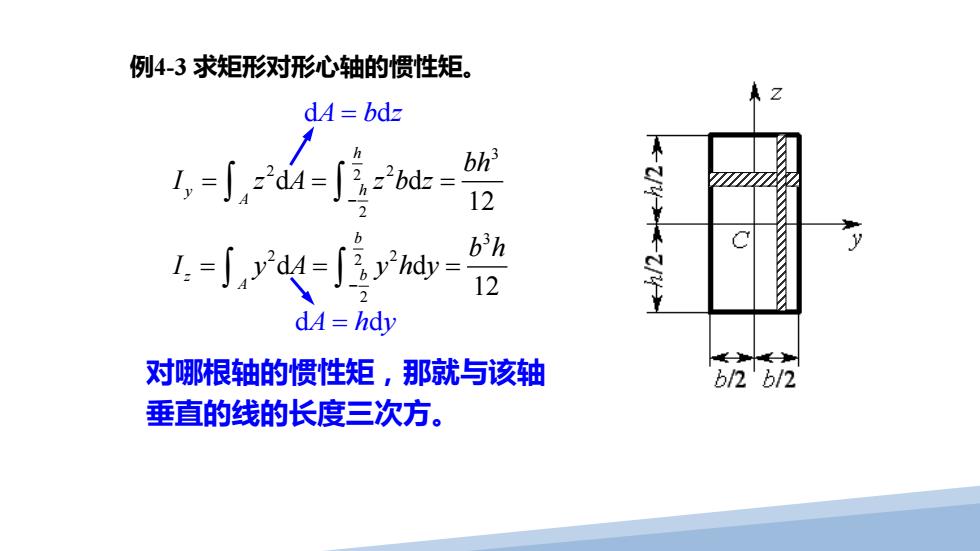
例4-3求矩形对形心轴的惯性矩。 dA=bdz 1,=∫dA=∫ibd= bh 12 L-可, bh C 12 d4=hdy 对哪根轴的惯性矩,那就与该轴 b/2b/2 垂直的线的长度三次方
例4-3 求矩形对形心轴的惯性矩。 3 2 2 2 2 3 2 2 2 2 d d 12 d d 12 h y h A b z b A bh I z A zbz b h I y A yhy − − = = = = = = ∫ ∫ ∫ ∫ d d A bz = 对哪根轴的惯性矩,那就与该轴 垂直的线的长度三次方。 d d A hy =

惯性半径 有时把惯性矩写成面积A与某一长度的平方的乘积,如 1,=A 1.=A 则 称为惯性半径 bh 对于矩形 1= A=bh 12 6- b/2'b/2
惯性半径 有时把惯性矩写成面积 A 与某一长度的平方的乘积,如 2 2 yy zz I Ai I Ai =⋅ =⋅ 则 y z y z I I i i A A = = 称为惯性半径 对于矩形 3 12 y bh I = A bh = 2 3 12 6 y y I h i h A = = =

三、惯性积:面积与其到两轴距离之积。 1=1yd 如果y或:是对称轴,则Iz=0 2 dA n 航
三、惯性积:面积与其到两轴距离之积。 d yz A I yz A = ∫ 如果 y 或 z 是对称轴,则 Iyz = 0 dA y z z y ρ O