
記 号 a,b,c,d数值系数,距离 A横面积 由中性轴至梁的边象纤维的距离 C扭转刚度(C=GJ) C1翘曲刚度(C1=ECw)》 Cw翘曲常数 D板或壳的弯曲刚度[D=3/12(1一2)] e偏心距,由形心至剪心的距离 E,E,E:弹性模量,折合模量,切线模量 F应力函数 &重力加速度 G剪切弹性模量 h板或壳的厚度,高度,距离 1,1。平面面积对于形心及剪心的极惯性矩 1x,1y,1x平面面积对于x,y,:轴的惯性矩 甲 1y平面面积对于x与y轴的惯性积 J扭转常数 为梁柱的轴向荷置因数(:=日),弹性基础模量,数值因子 1长度,跨度 L折合长度 m,n整数,数值系数 m:沿:轴每单位长疲的扭矩最度 M弯矩,力偶 M:扭力偶或扭矩 Mx,My,My板或壳每单位长度的弯矩及扭矩 n安至系数 N梁丙的剪力,法向力 Nx,Ny,Ny板或壳的中面每单位长度的法向力与剪力 xii

P,9分布荷重的强度,压力 P集中力,梁-柱中的轴向力 Pr临界荷重 ?梁丙的剪力,集中力 Qx,Qy板或壳每单位长度的剪力 ”迴转牛径,壳的曲率牛径,牛径 R华径,反力 ·核心牛径(:=Z/A),距离 5轴向力 t厚度,时间,祖度 T功,张力 “梁-柱的轴向荷重因数(“=1/2) ,",W在x,y,玄方向的位移 U应变能 ”,w切向与径向位移 V梁内的剪力 地梁内的翘曲位移 x,y,云直角坐标 Z截面模量(Z=I/c) α,B角,数值系数,比值,弹簧常数,端点约束采数 Y 剪应变,单位体积的重量,弹簧常数,数值因子 6挠度 B正应变,热膨张系数 8x,By,8x在x,y,云方向的正应变 7,入,中,x,中梁-柱的放大因数 日角,角坐标,单位长度的扭转角 1距离,数值因子 v泊松比 ,7,5直角坐标 P曲率牛径 0正应力 0x,0,0:在x,y,z方向的正应力 。xiiⅱ

0。柱的平均压应力 :临界荷重时的压应力 Cult 极限应力 Ow资用应力 Ox.P.屈服应力 t剪应力 xy,y,Yx与x,y,z轴垂直的面上平行于y,,轴的剪应小 中角,角坐标,杆的扭转角 中角 X。壳的曲率的改变 a振动的圆频率 ω,翘曲函数

目录 第二版序 ⅲ 第一版序 V 記号 xii 第一章梁柱 1.1.引言…… ……1 1.2.梁-柱的微分方程…1 1.3.有一横向集中荷重作用的梁-柱 ……………………… $1.5.连续横向荷重..9 $1.6.由力偶引起的梁-柱的弯曲…13 $1.7.挠度的近似公式....5 $1.8.两端固定的梁-柱……16 $1.9.有弹性约束的梁-柱18 $1.10.有轴向荷重的连续梁...0 $1.11.三角级数的应用…26 $1.12.初弯曲对挠的影响33 $1.13.可应力的决定….0 第二章杆与框架的弹性屈曲…49 $2.1.欧拉的柱公式.......49 $2.2.由另一形式的微分方程决定临界荷重54 2.3.用梁-柱理论计算临界荷重…63 $2.4.框架的屈曲·66 $2.5.连续梁的屈曲…71 52.6.弹性支座上的连续梁的屈曲 2.7.屈曲杆的大挠度(弹性线)…81 $2.8.能量法87 2.9.以能量法计算近似的临界荷重4 .yii

2.10.在弹性基础上的杆的屈曲…100 $2.11.在中间压力作用下杆的屈曲104 $2.12.在分布轴向荷重作用下杆的屈曲……107 $2.13.弹性基础上的杆在分布轴向荷重作用下的屈曲……114 2.14.变面杆的屈曲120 $2.15.用逐大近法决定临界荷重124 $2.16.横截面连续变化的杆134 $2.17.剪力对临界荷重的影响…141 $2.18.组合柱的屈曲…144 2.19.螺旋弹簧的屈曲…...151 $2.20.杆系的稳定性154 $2.21.非保守力的情形163 2.22.在变化轴向力作用下稜柱杆的稳定性………169 第三章杆的非弹性屈曲 175 3.1.非弹性弯曲…… 175 3.2.在轴向荷重联合作用下的非弹性弯曲 180 3.3.杆的非弹性屈曲,基本情形………… 188 3.4.具有其他端点条件的杆的非弹性屈曲 196 第四章实驗与設計公式… 199 4.1.柱的实验……… 199 4.2.以理想柱的公式作为设计柱的基础 207 $4.3.设计柱的经验公式… 209 $4.4.以所设的缺陷作为设计柱的根据… 211 4.5.各种端点条件 4.6.组合柱的设计 第五章扭轉屈曲 227 5.2.开口薄壁杆件的纯扭转 5.3.开口薄壁杆件的非均匀扭转233 $5.5.由于扭转与弯曲的屈曲245 5.6.具有连续弹性支承的杆由于扭转与弯曲的屈曲………253 .yiii

5.7.在压力与端弯矩作用下的扭转屈曲261 第六章梁的横向屈曲… 6.1.横向屈曲的微分方程 ..269 56.2.纯弯曲梁的横向屈曲 271 56.3.悬臂梁的横向屈曲 275 6.4.简支工字梁的横向屈曲 6.5.简支狭长矩形截面梁的向屈曲286 56.6.横向屈曲的其他情形…… ..288 $6.7.工字梁的非弹性向屈曲…290 第七章圓环、曲杆与拱的屈曲 297 7.1.圆形细曲杆的弯曲…………… 7.2.应用三角级数分析薄圆环的弯曲 7.3.均匀压力对圆环弯曲的影响………… 306 7.4.在均布外压下圆环及管的屈曲308 $7.5.以所设的缺陷为根据设计受均布外压作用的管子…………313 7.6.均匀受压圆拱的屈曲 $7.7.其他形式的…322 $7.8.很扁平的曲杆的屈曲325 $7.9.两种金属组合小条的屈曲330 7.10.圆形轴线曲杆的横向屈曲.333 第八章薄板的弯曲…………………339 $8.1.板的纯弯曲…339 $8.2.在分布横向荷重作用下板的弯曲346 8.3.板受弯曲与拉伸或压缩的联合作用353 8.4.板弯曲的应变能355 $8.5.简支边矩形板的挠度361 8.6.具有微小初弯曲的板的弯曲…364 8.7.板的大度 366 第九章薄板的屈曲………369 9.1.临界荷重的计算方法.369 9.2.在一个方向均匀受压的简支短形板的屈曲372 9.3.在两垂直方向受压的简支矩形板的屈曲377 .ix

59.4.承受均布压力的矩形板的屈曲:与压力方向垂直的两对边 简支,而沿其余的两边有各种的边界条件………381 9.5.两对边简支井在与这两边平行的方向均匀受压的矩形板 $9.6.在弯曲与压缩联合作用下简支短形板的屈曲…396 9.7.在剪应力作用下矩形板的屈曲403 9.8.矩形板屈曲的其他情形410 9.9.圆板的屈曲413 9.10.其他形状的板的屈曲416 9.11.以肋条加强的板的稳定性418 $9.12.超过比例极限的板的屈曲…435 $9.13.屈曲板的大挠度437 $9.14.屈曲板的极限强度..445 $9.15.板的屈曲实验.451 $9.16.板屈曲理论的实际应用457 第十章薄壳的弯曲………468 $10.1.壳上体元的变形468 10.2.圆柱形壳的对称变形…471 10.3.圆柱形壳的无伸长的变形…473 $10.4.柱形壳的变形的一般情形477 10.5.球形壳的对称变形 482 第十一章壳的屈曲………486 11.1.圆柱形壳在均匀轴向压缩下的对称屈曲…486 $11.2.圆柱形壳由于不稳定性的无伸长弯曲形式………490 $11.3.在均匀轴向压力作用下圆柱形壳的屈曲(一般情形)……491 11.4.圆柱形壳轴向受压的实验497 $11.5.均匀横向外压作用下圆柱形壳的屈曲503 $11.6.受弯曲的或偏心受压的圆柱形壳…512 11.7.曲薄板的轴向压缩516 11.8.在剪力或剪力与轴向应力共同作用下的曲薄板…519 $11.9.在轴向压缩下加劲柱壳的屈曲521 11.10.在轴向压力与均匀横向压力共同作用下圆柱形壳的屈曲…526 11.11.受扭转的圆柱壳的屈曲…531

511,12,锥形壳的屈曲…541 511,13.均匀受压的球形壳的屈曲…545 附录 表A-1函数中(4),中(4),x(w)表……553 表A-2函数(4)与入(4)表…561 表A-3截面的性假………………562 内容索引…563 3 、 E ·xi

第一章 梁-柱 51.1.引营 在弯曲的初等理論中,梁的应力和挠度与作用的荷重成正比, 这要求梁由弯曲引超的变形不影响荷重的作用.例如,图1.1a中 只承受横向荷重(Q:与Q2)的梁,微小的挠度61与2及荷重的 铅直作用钱的稍微改变,对弯矩与剪力的影响无关紧要,于是,就 可以在梁的原有形状的基 础上,来計算挠度、应力与 弯矩等等在这些条件下, 并設材料服从胡克定律, (a) 則挠度与作用的荷重成正 比,且迭加原理可以适用: 1Q2 即最終的变形为各荷重单 独所产生的变形之和. (6) 当軸向和横向荷重同 图1.1 时作用于梁时(图1.16),情况完全不同.梁的弯矩、剪力,应力及 挠度并不与軸向荷重的大小成比例;而且,它們的值与所产生的挠 度的大小有关,且轴向荷重作用的稍微偏心就对它們有很大的影 响。同时承受轴向压力和横向荷重的梁称为梁-柱。在这第一一章 内,将分析在各种支承与加截状况下具有对称横截面的梁-柱”. §12.梁-柱的微分方程 用以分析梁-柱的基本方程可由开究图1.2a中的梁而推出. 1)对于承受轴向拉力的粱的分析,可参阅Timoshenko,Strength of Materials, 3d ed.,part lI,p.41,D.Van Nostrand Company,Inec.,Princeton,N. J,1956. 1
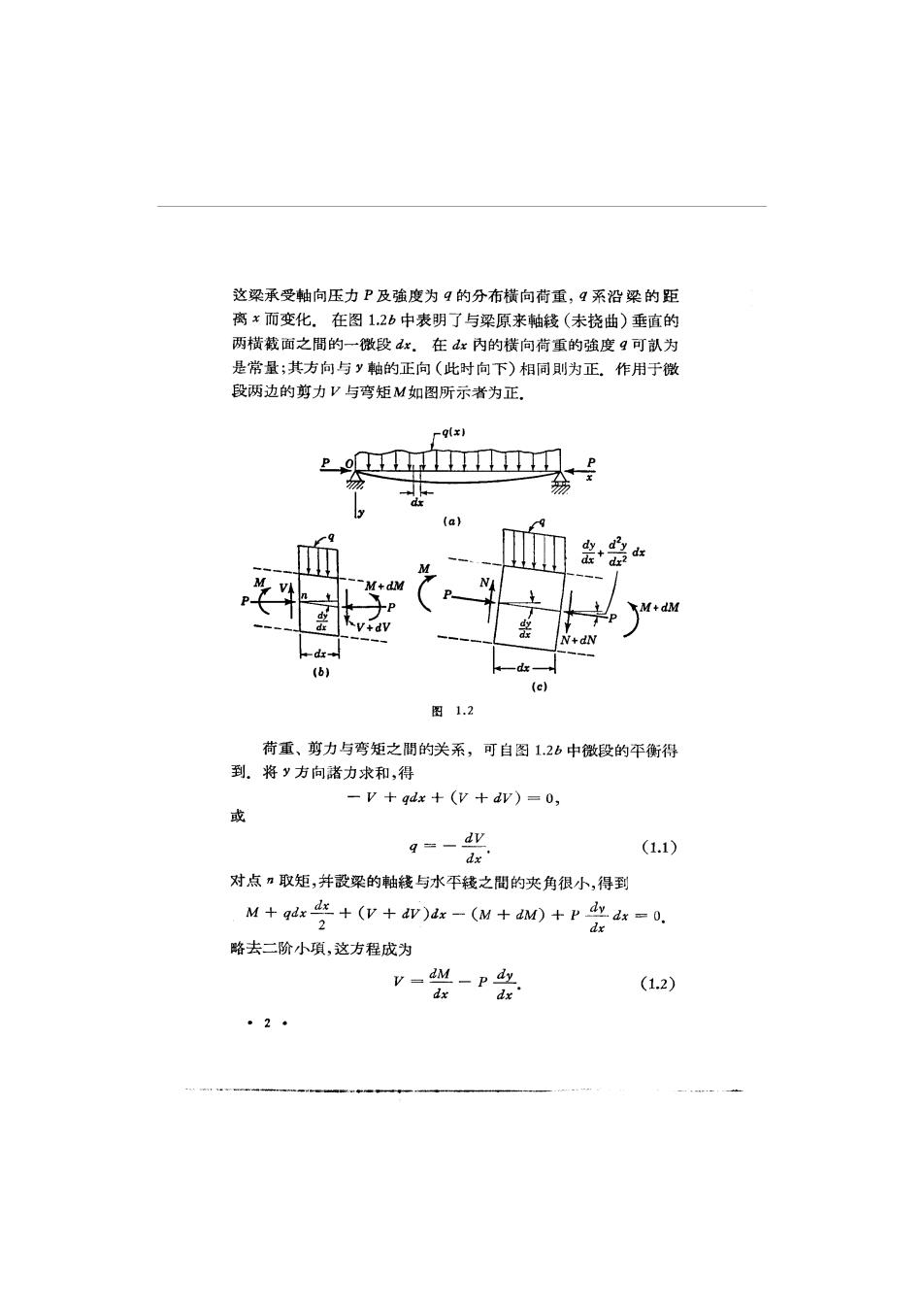
这梁承受軸向压力P及強度为4的分布横向荷重,9系沿染的距 离x而变化.在图12b中表明了与梁原来軸钱(未挠曲)垂直的 两横载面之間的一微段dx.在x内的横向荷重的強度g可认为 是常量;其方向与y軸的正向(此时向下)相同則为正。作用于微 段两边的剪力V与弯矩M如图所示者为正 -q(x) Po层 P (a) M+dM +dN dx (c) 图1.2 荷重、剪力与弯矩之間的关系,可自图1.2b中微段的平衡得 到。将y方向諸力求和,得 -v+qdx+(v+dv)=0, 或 9=、dy (1.1) dx 对点n取矩,并設梁的軸後与水不钱之間的夹角很小,得到 M+qdx+v)dx-(M+dM)+p4dx=0. 2 dx 略去二阶小項,这方程成为 vdM-p dy (1.2) dx dx 。2