同济大学：《结构动力学》课程教学资源（教案讲义）Lecture 04 Response to harmonic and periodic excitations - Application

Structural Dynamics Lecture 4 Response to harmonic and periodic excitations: Application 目 同榜大学 上水工程学院 COLLEGE OF CIVIL ENGINEERING

Structural Dynamics Lecture 4 Response to harmonic and periodic excitations: Application

Contents Response of SDOF to harmonic excitation: application Identify the natural frequency and damping ratio Vibration measurements Earthquake Isolation ·Vibration Isolation Response of SDOF to periodic excitation 闺 土本2程学院

Contents  Response of SDOF to harmonic excitation: application • Identify the natural frequency and damping ratio • Vibration measurements • Earthquake Isolation • Vibration Isolation  Response of SDOF to periodic excitation

Field test of full-scale structures:Vibration shaker Rotating machine with eccentric mass p(1)=(meo)sin(ot) m。:maSS e:eccentricity @rotating frequency 35 kg vibration shaker Max.Force generated1500T 闺 土本程李悦

35 kg vibration shaker Max. Force generated1500T  Field test of full-scale structures: Vibration shaker • Rotating machine with eccentric mass       2 sin e p t m e t    : : : m mass e e eccentricity  rotating frequency

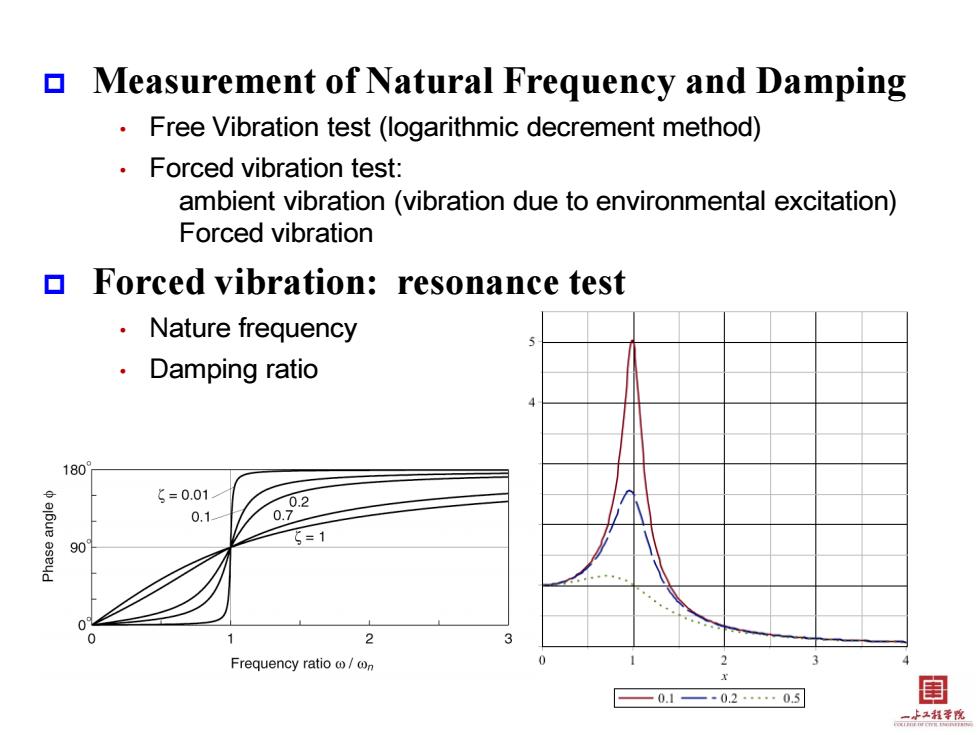
Measurement of Natural Frequency and Damping Free Vibration test(logarithmic decrement method) Forced vibration test: ambient vibration(vibration due to environmental excitation) Forced vibration Forced vibration:resonance test Nature frequency Damping ratio 180 g=0.01 0.1 002 90 5=1 Frequency ratio/n —0.1-02…0.5 目 二水二程季院

 Measurement of Natural Frequency and Damping • Free Vibration test (logarithmic decrement method) • Forced vibration test: ambient vibration (vibration due to environmental excitation) Forced vibration  Forced vibration: resonance test • Nature frequency • Damping ratio

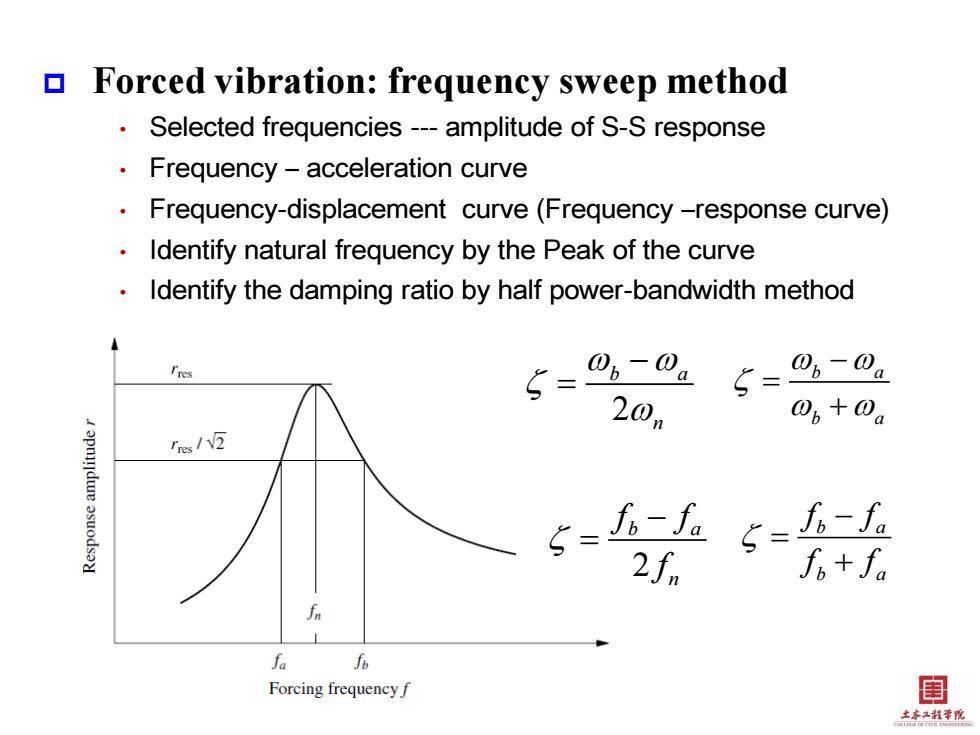
Forced vibration:frequency sweep method Selected frequencies---amplitude of S-S response Frequency-acceleration curve Frequency-displacement curve(Frequency -response curve) Identify natural frequency by the Peak of the curve Identify the damping ratio by half power-bandwidth method 5-0。-0 5=0-02 20n 0b+0a es/W② 6=f上5-人- 2f f6+f。 fa 6 Forcing frequencyf 闺 土亦工鞋季悦

 Forced vibration: frequency sweep method • Selected frequencies --- amplitude of S-S response • Frequency – acceleration curve • Frequency-displacement curve (Frequency –response curve) • Identify natural frequency by the Peak of the curve • Identify the damping ratio by half power-bandwidth method 2 b a n       b a b a         2 b a n f f f    b a b a f f f f    

Equivalent viscous damping f+fD+f=f。 ∫fid+∫fn+jrau=Sfchu Conclusion:In steady state response,the energy input to the system due to the applied force is dissipated in viscous damping 目 主求2相季院

 Equivalent viscous damping • Conclusion: In steady state response, the energy input to the system due to the applied force is dissipated in viscous damping I D s p f f f f    I D s p f du f du f du f du       

Energy dissipated in viscous damping in each vibration cycle. E=[Iodu-"(cu)idt=eu'dr 2π10 2π10 =c[ou,cos(ot-)di =πC0uo =25 ku Energy dissipated in viscous damping is proportional to the square of motion amplitude,and damping ratio and w 土本工相季汽

• Energy dissipated in viscous damping in each vibration cycle.     2 / 2 / 2 0 0 2 / 2 0 0 2 0 2 0 cos 2 D D n E f du cu udt cu dt c u t dt c u ku                                    • Energy dissipated in viscous damping is proportional to the square of motion amplitude, and damping ratio and w

In steady state response,the energy input to the system due to the applied force is dissipated in viscous damping E,=Sp()du=p(t)idr (po sin )[ou cos(di sm28风-28） uo Po/k 目 土本之相学院

• In steady state response, the energy input to the system due to the applied force is dissipated in viscous damping         2 / 0 2 / 0 0 0 2 0 0 0 sin cos sin 2 I n E p t du p t udt p t u t dt p u ku                                 0 0 sin 2 2 / d n n u R p k                     

Potential energy by spring element Es =Jfdu=(kut)idr k[u sin(t)]Lou cos(t-)]dt=0 Energy by inertia force Ex -fdu-(miyidr -m[-oiusin(t-)][ou cos(-)]di=0 2π/0 目 土本程李悦

• Potential energy by spring element       2 / 0 2 / 0 0 0 sin cos 0 E f du ku udt S s k u t u t dt                           • Energy by inertia force       2 / 0 2 / 2 0 0 0 sin cos 0 E f du mu udt K I m u t u t dt                          

Why SS displacement amplitude is bounded no matter how small the damping The input energy varies linearly with the displacement The dissipated energy varies quadratically with the displacement Ep E EI=ED Amplitude 目 主京2相季院

 Why SS displacement amplitude is bounded no matter how small the damping • The input energy varies linearly with the displacement • The dissipated energy varies quadratically with the displacement