西南交通大学：《工程塑性力学》课程教学资源（教案讲义）第三章 应力和应变分析（3.1）应力分析

3.1.1应力张量及其分解 一点的空间应力状态 定义：通过一点P取单元体，各个面上应力状况的集合 x面的应力： y面的应力： Oy, z面的应力： 在切应力的下标中，第一个表示所在平面， 第二个表示应力的方向

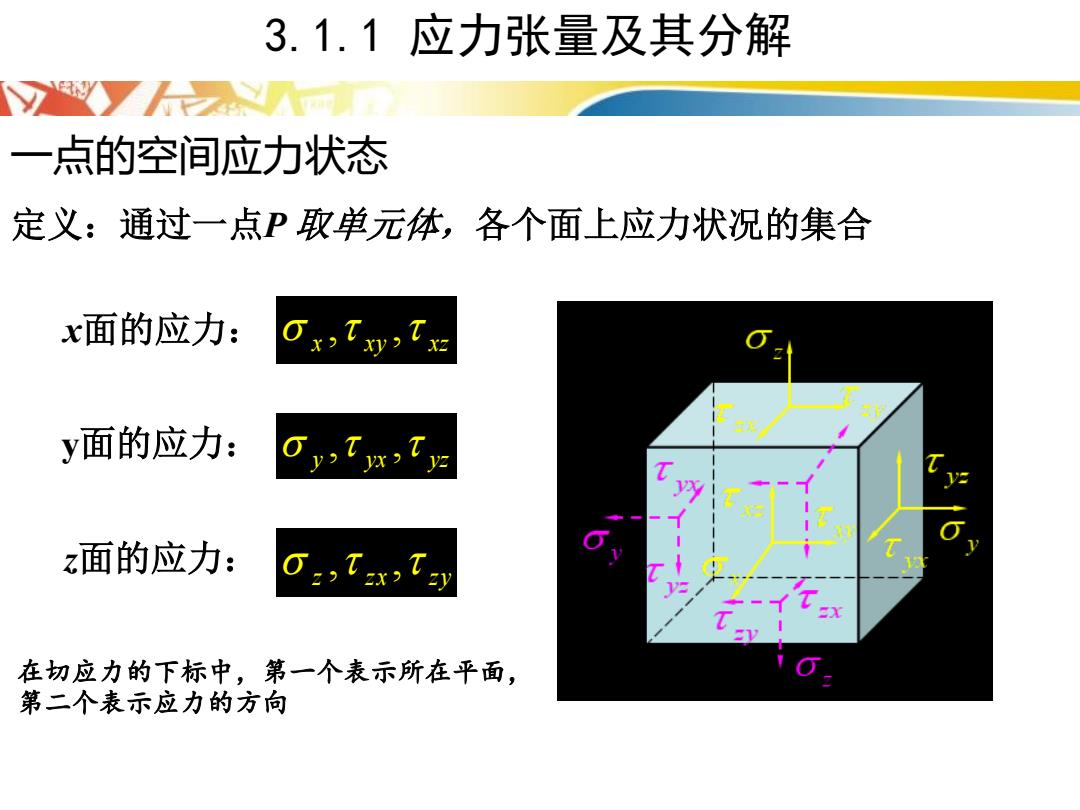
3.1.1 应力张量及其分解 一点的空间应力状态 定义：通过一点P 取单元体，各个面上应力状况的集合 x xy xz x面的应力：  , , y yx yz  , , z z x z y  , , y面的应力： z面的应力： 在切应力的下标中，第一个表示所在平面， 第二个表示应力的方向

3.1.1应力张量及其分解 72m 正负号规定： 正应力分量同前，拉为正、压为 负； 切应力分量重新规定： 正面（外法线与坐标轴指向一致) 上切应力分量与坐标轴正向一致， 为正。 负面上切应力分量与坐标轴负向 一致时，切应力为正，反之为负

正负号规定： 正应力分量同前，拉为正、压为 负； 切应力分量重新规定： 正面（外法线与坐标轴指向一致） 上切应力分量与坐标轴正向一致， 为正。 负面上切应力分量与坐标轴负向 一致时，切应力为正，反之为负。 3.1.1 应力张量及其分解

3.1.1应力张量及其分解 定义：一点的应力状态可由九个应力分量来描述，这些分量构成 一个二阶对称张量，称为应力张量。 上式中左边是工程力学的习惯写法，右边是弹性力学的习惯写法 写法：采用张量下标记号的应力写法 根据切应力互等定理，独立的分量只有6个，即： Oy

一点 的应力状态可由九个应力分量来描述，这些分量构成 一个二阶对称张量，称为应力张量。 (3 −1)                     x z y z zz x y y y y z x x x y x z z y z z x y y y z x x y x z                   或 上式中左边是工程力学的习惯写法，右边是弹性力学的习惯写法 定义： 写法： 采用张量下标记号的应力写法 3.1.1 应力张量及其分解 根据切应力互等定理，独立的分量只有6个，即： x y z xy yz zx  ,  ,  ,  ,  , 

3.1.1应力张量及其分解 把坐标轴×、y、z分别用x1、X2、×3表示，或简记为×(i=1,2,3), =0,=0(3-2) T(es) 4e3 3 03] 竹 032 013 023 011 012 021 022 e2 T(e1) T(e2) By Sanpaz-Own work,CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=5668647

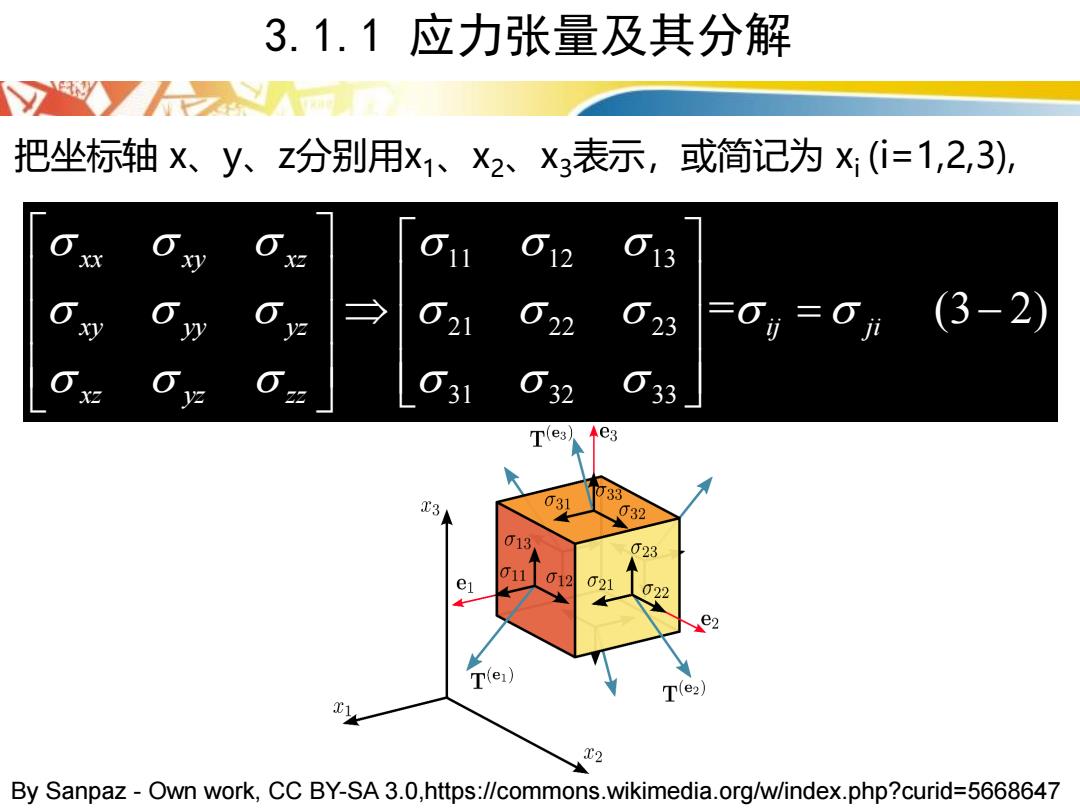
把坐标轴 x、y、z分别用x1、x2、x3表示，或简记为 xi (i=1,2,3), 11 12 13 21 22 23 31 32 33 = (3 2) xx xy xz xy yy yz ij ji xz yz zz                            = −       By Sanpaz - Own work, CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=5668647 3.1.1 应力张量及其分解

3.1.1应力张量及其分解 静水“压力”：011=022=033=0 注意：静水压力既可是压应力，也可是拉应力 ●在静水压力作用下，应力一应变间服从弹性规律，且不会屈服 不会产生塑性变形。 不产生塑性变形的部分 反映静水“压力” 应力 产生塑性变形的部分 反映应力偏张量

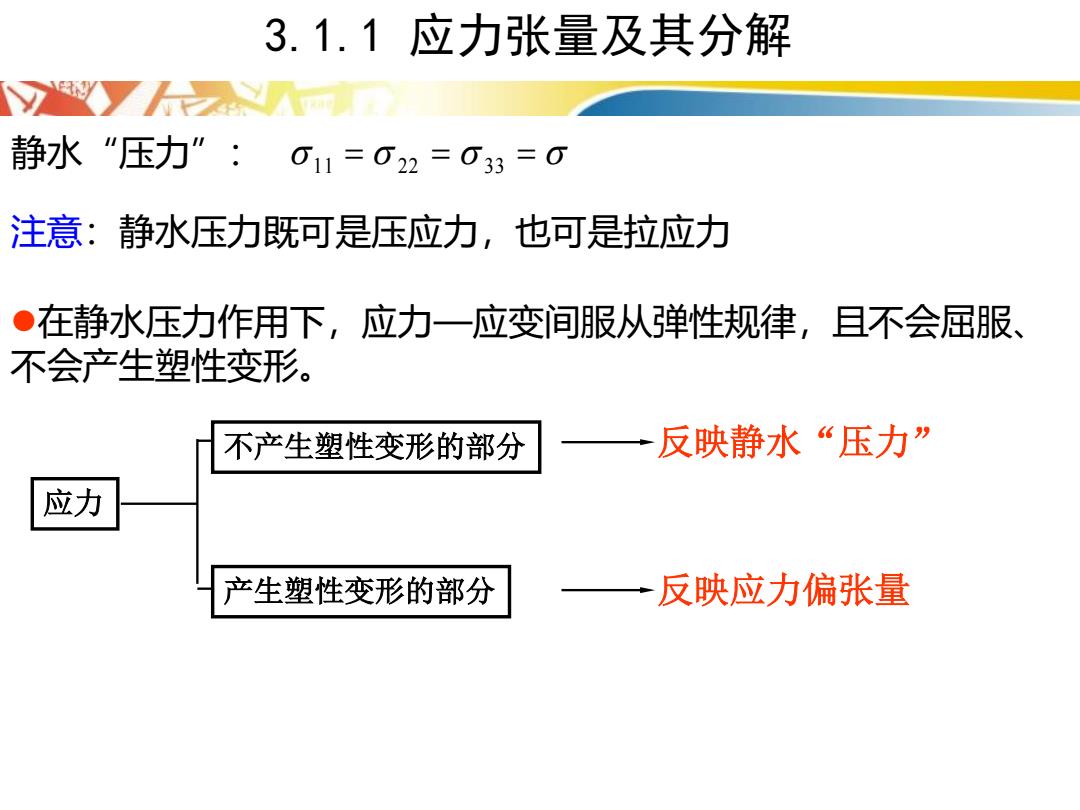
静水“压力”：     11 22 33 = = = 3.1.1 应力张量及其分解 注意：静水压力既可是压应力，也可是拉应力 ⚫在静水压力作用下，应力—应变间服从弹性规律，且不会屈服、 不会产生塑性变形。 应力 不产生塑性变形的部分 产生塑性变形的部分 反映静水“压力” 反映应力偏张量

3.1.1应力张量及其分解 72 平均正应力 m (11+02+)=30k (3-4) 应力张量可作如下分解： 13 033 一0m

平均正应力 = ( + + ) = (3 - 4) 3 1 3 1  m  1 1  2 2  3 3  k k 应力张量可作如下分解： 11 12 13 11 12 13 21 22 23 21 22 23 31 32 33 31 32 33 0 0 0 0 0 0 m m m m m m                               −       = + −             −       3.1.1 应力张量及其分解

3.1.1应力张量及其分解 应力球张量 与单元体的体积变形有关 其中： 1,当i=j, 或 0,当i≠j。 (3-6) 单位球张量 应力球张量，它表示各方向承受相同拉（压）应力 m 而没有剪应力的状态

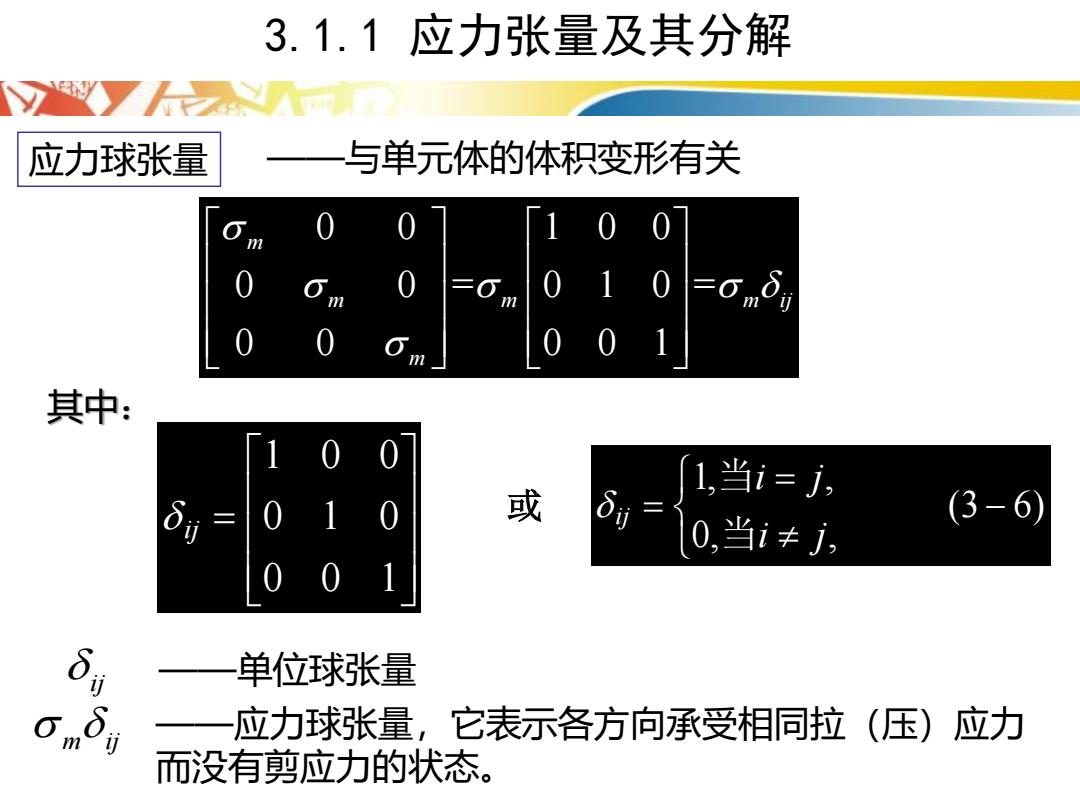
应力球张量 0 0 1 0 0 0 0 = 0 1 0 = 0 0 0 0 1 m m m m ij m                   ——与单元体的体积变形有关 其中： (3 6) 0, , 1, , −     = = i j i j ij 当 当            = 0 0 1 0 1 0 1 0 0  ij 或 ij  ——单位球张量  m ij ——应力球张量，它表示各方向承受相同拉（压）应力 而没有剪应力的状态。 3.1.1 应力张量及其分解

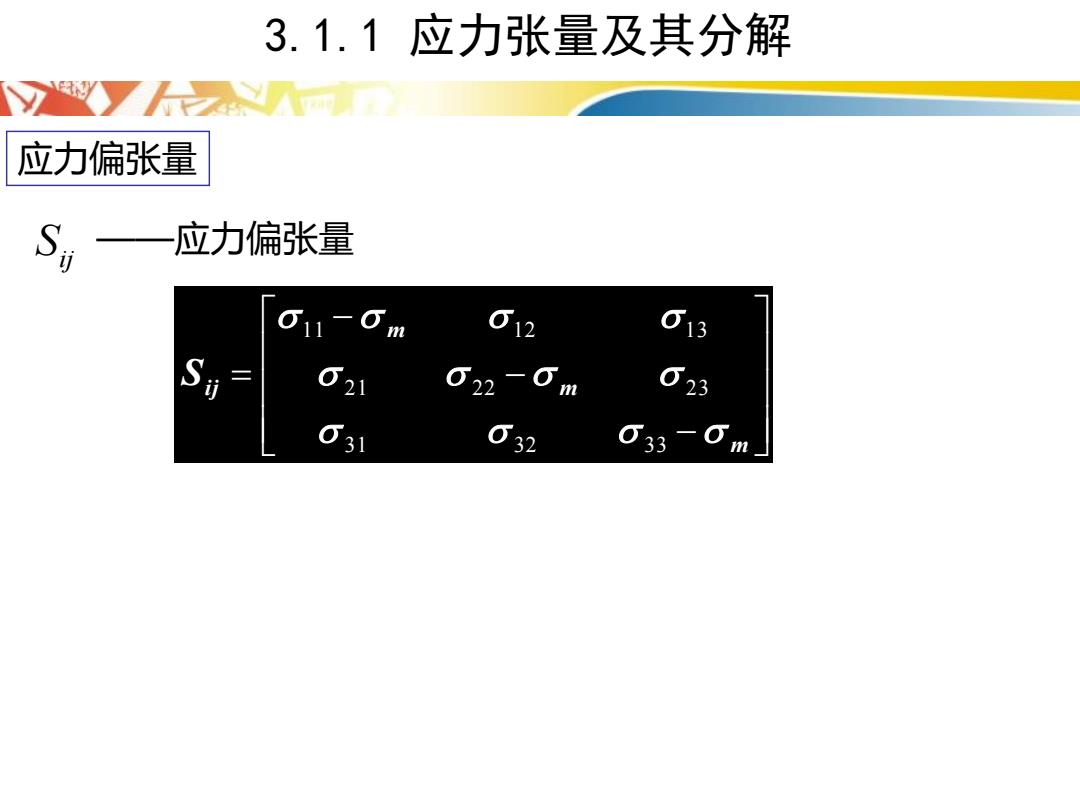
3.1.1应力张量及其分解 w了2m 应力偏张量 S,— 应力偏张量 012 12 3 032 033 -O

应力偏张量 ij S ——应力偏张量           − − − = m m m Si j             3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 3.1.1 应力张量及其分解

3.1.1应力张量及其分解 应力张量分解： 用张量符号表示： =0m (3-5) 说明： 应力球张量 一与单元体的体积变形有关 应力偏张量 与单元体的形状改变有关 材料进入塑性后，单元体的体积变形是弹性的，只与应力球张量有 关；而与形状改变有关的塑性变形侧是由应力偏张量引起的

用张量符号表示： , (3 5) ij m ij ij    = + − s 应力张量分解： 11 12 13 11 12 13 21 22 23 21 22 23 31 32 33 31 32 33 0 0 0 0 0 0 m m m m m m                               −       = + −             −       说明： 材料进入塑性后，单元体的体积变形是弹性的，只与应力球张量有 关；而与形状改变有关的塑性变形则是由应力偏张量引起的 。 应力球张量 应力偏张量  m ij ——与单元体的体积变形有关 ij S ——与单元体的形状改变有关 3.1.1 应力张量及其分解

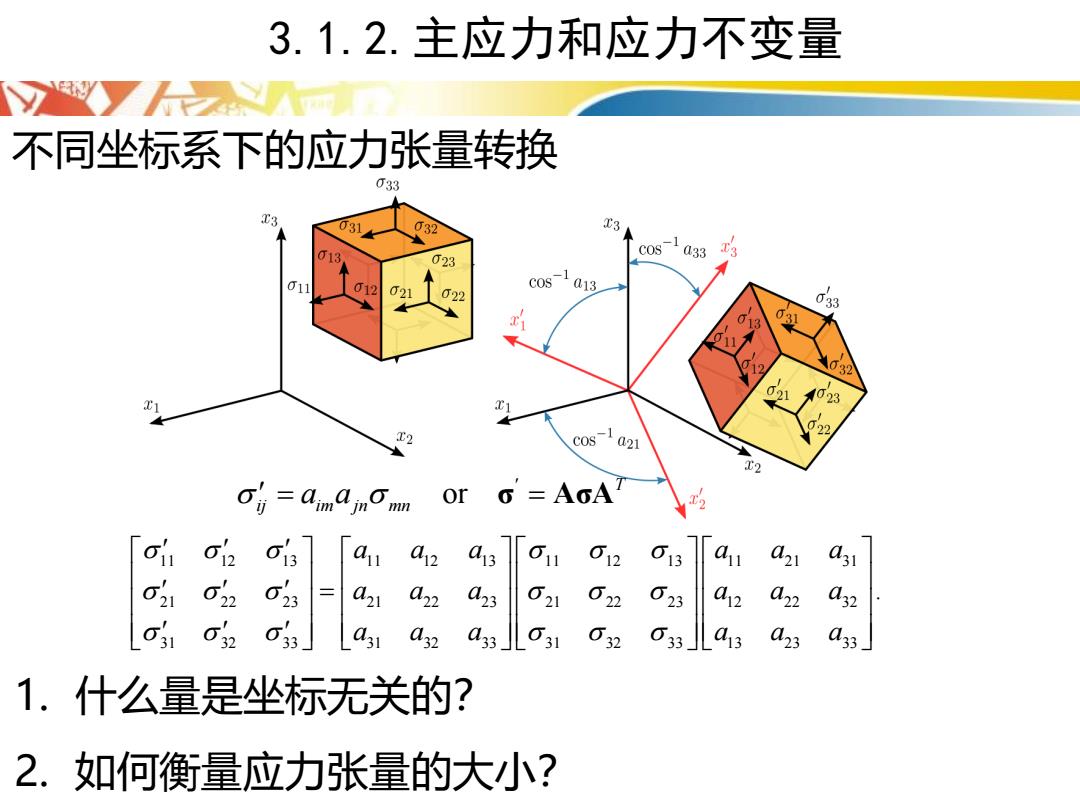
3.1.2.主应力和应力不变量 不同坐标系下的应力张量转换 033 032 713 023 cos-1a33 3 1 c0s-1a13 022 13 6 011 012 61 103 c0s-1a21 T2 or O=AcA a 3 02 3 av azi a31 0 6 a21 a22 03 61 62 623 a2 a22 a32 a31 a32 a33 031 032 033 a13 d23 1.什么量是坐标无关的？ 2.如何衡量应力张量的大小？

3.1.2.主应力和应力不变量 11 12 13 11 12 13 11 12 13 11 21 31 21 22 23 21 22 23 21 22 23 12 22 32 31 32 33 31 32 33 31 32 33 13 23 33 . a a a a a a a a a a a a a a a a a a                                         =            or T ij im jn mn   a a   = = σ AσA 不同坐标系下的应力张量转换 1. 什么量是坐标无关的？ 2. 如何衡量应力张量的大小？