
第13章质点系动能定理 力的功 动能 动能定理与机械能守恒 功率、功率方程、机械效率 动力学普遍定理的综合应用 讨论
□ 力的功 □ 动能定理与机械能守恒 □ 功率、功率方程、机械效率 □ 讨论 □ 动能 第13章 质点系动能定理 □ 动力学普遍定理的综合应用

对点的动量矩: Lo=Mo(mv) 对轴的动量矩:Lz=Mz(mw) 动量矩定理: 立M.网 投影式: i dLs=ZM,(F) dt dL=ΣM,(oy d dL=ΣM(Fo
L M (mv) O = O L M (mv) Z = Z 对点的动量矩: 对轴的动量矩: 动量矩定理: = = n i O O M F dt dL 1 ( )
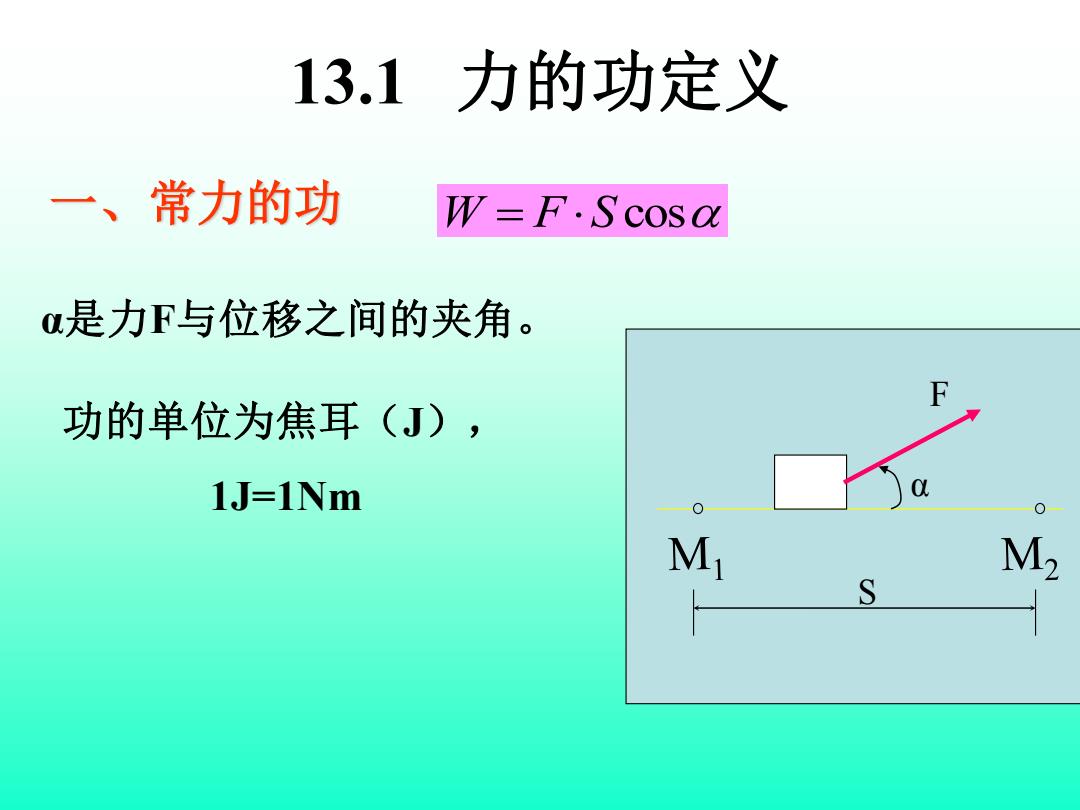
13. 1力的功定义 一、常力的功 W=F.Scosa α是力F与位移之间的夹角。 F 功的单位为焦耳(J), 1J=1Nm M M S
一、常力的功 F S α W = F S cos α是力F与位移之间的夹角。 功的单位为焦耳(J), 1J=1Nm 13.1 力的功定义
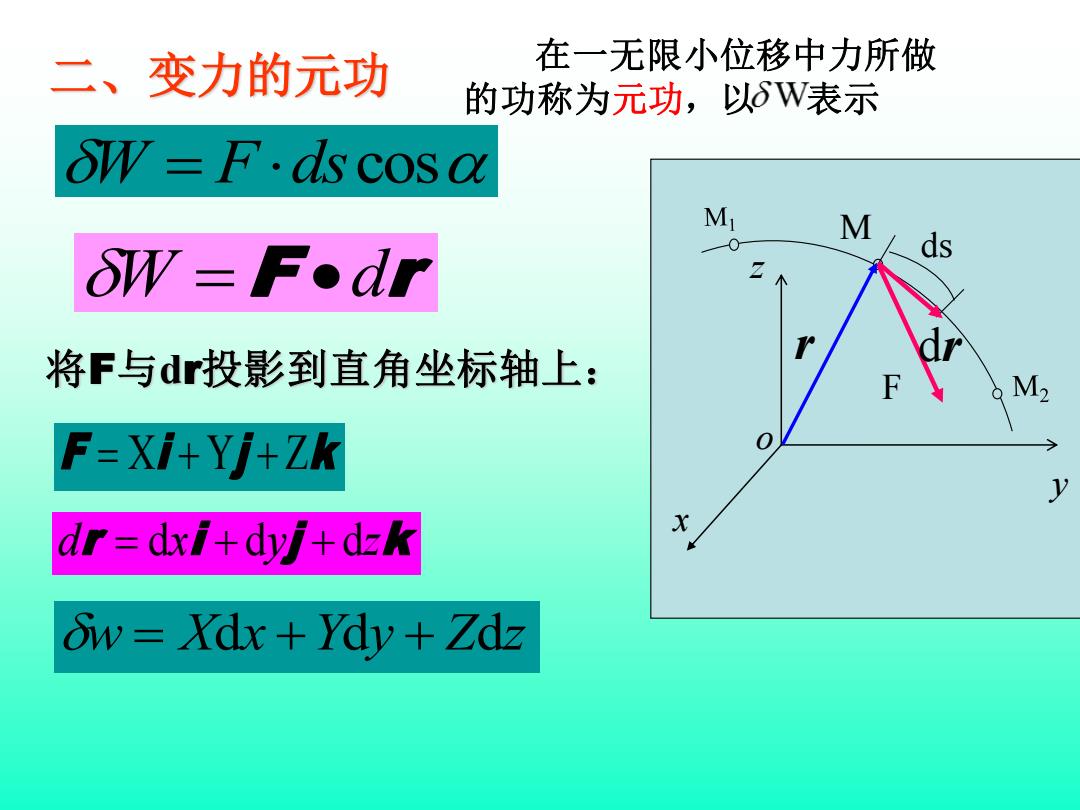
二、变力的元功 在一无限小位移中力所做 的功称为元功,以6W表示 δW=F.ds cos a M M δW=F●dr ds 将F与dr投影到直角坐标轴上: F F=Xi+Yj+Zk 0 y dr=dxi+dyj+dzk ow=Xdx+Ydy+Zdz
二、变力的元功 M F ds W = Fdscos dr W =F •dr y o x z r 将F与dr投影到直角坐标轴上: F = Xi + Yj + Zk dr = dxi + dyj + dzk w = Xdx +Ydy + Zdz 在一无限小位移中力所做 的功称为元功,以 表示

力F在曲线路程M,M中作功为 w=∫cos ads=∫F,ds M M M M1 ds (自然形式表达式) F M =「F.d (矢量式) 0 M y M2 Xdx+Ydy +Zd Mi (直角坐标表达式)
力 在曲线路程 中作功为 (自然形式表达式) (矢量式) (直角坐标表达式) M F ds dr y o x z r

质点M受个力E,F,,F作用合力为=∑F,则合力R 的功 M M W=∫πf=∫(匠+E++F)而 Mj M M 万亦+了万亦++了万而=形,+W,++W M M M 即 W-∑W 在任一路程上,合力的功等于各分力功的代数和
质点M 受n个力 作用合力为 则合力 的功 即 在任一路程上,合力的功等于各分力功的代数和

3.平面运动刚体上力的功 刚体平动时: w =Fd=Fd z X 0 2
3. 平面运动刚体上力的功 刚体平动时: i i i i c W F r F r = d = d o x y z C i Fi c r d c r d
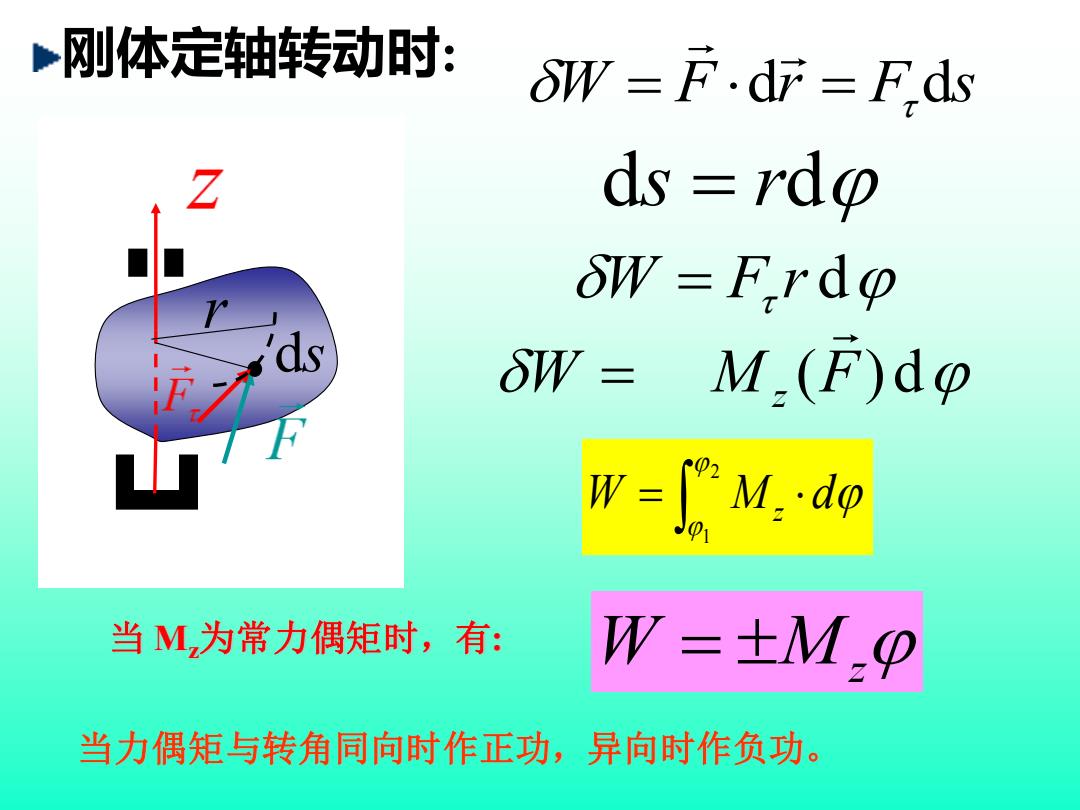
刚体定轴转动时: oW =F.dr =Fds ds rdo δW=F,rdp δW=M.(F)dp M.do 当M为常力偶矩时,有: W=±Mp 当力偶矩与转角同向时作正功,异向时作负功
刚体定轴转动时: W = F r d W M z (F)d = W F dr F ds = = ds = rd ds r = 2 1 W M z d 当 Mz为常力偶矩时,有: W = M z 当力偶矩与转角同向时作正功,异向时作负功
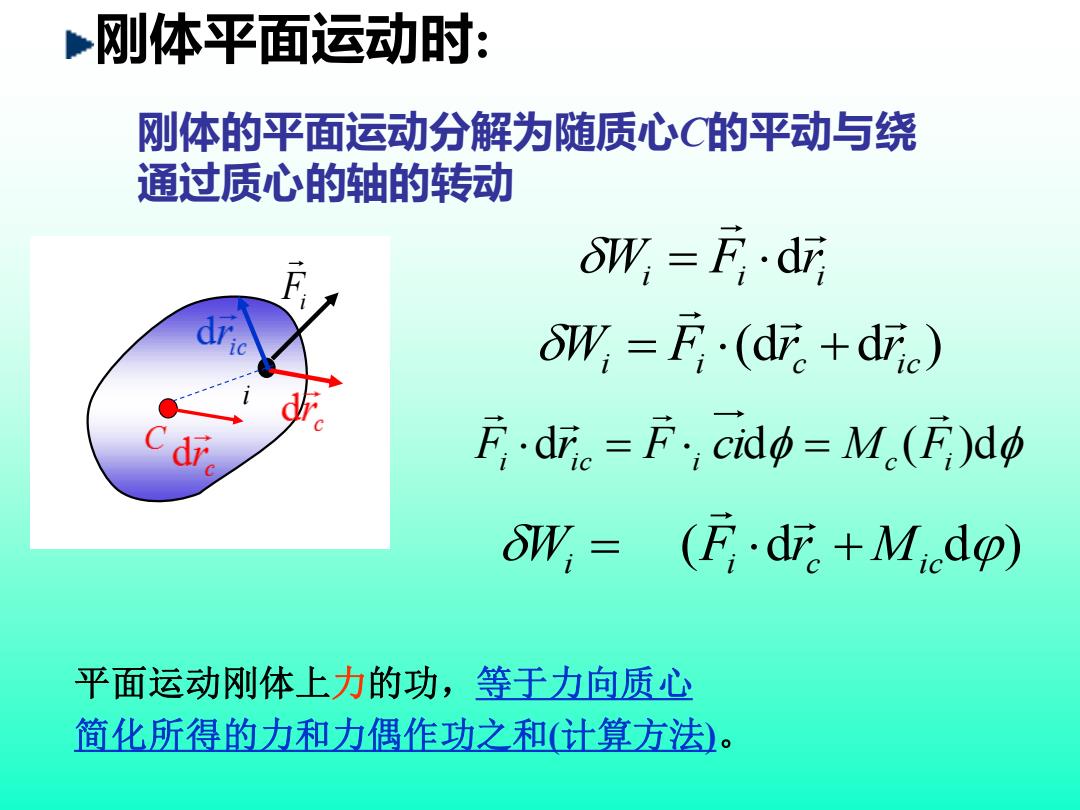
刚体平面运动时: 刚体的平面运动分解为随质心C的平动与绕 通过质心的轴的转动 δW,=F·d oW,=E,·(d。+dc) Fdf。=F,cidφ=M(E)dp oW=(E·d.+Mdp) 平面运动刚体上力的功,等于力向质心 简化所得的力和力偶作功之和(计算方法)
刚体平面运动时: 刚体的平面运动分解为随质心C的平动与绕 通过质心的轴的转动 i i i W F r = d ( d d) i i c Mi c W = F r + (d d ) i i c ic W F r r = + Fi i Fi dri c F i cid Mc (Fi )d = = 平面运动刚体上力的功,等于力向质心 简化所得的力和力偶作功之和(计算方法)
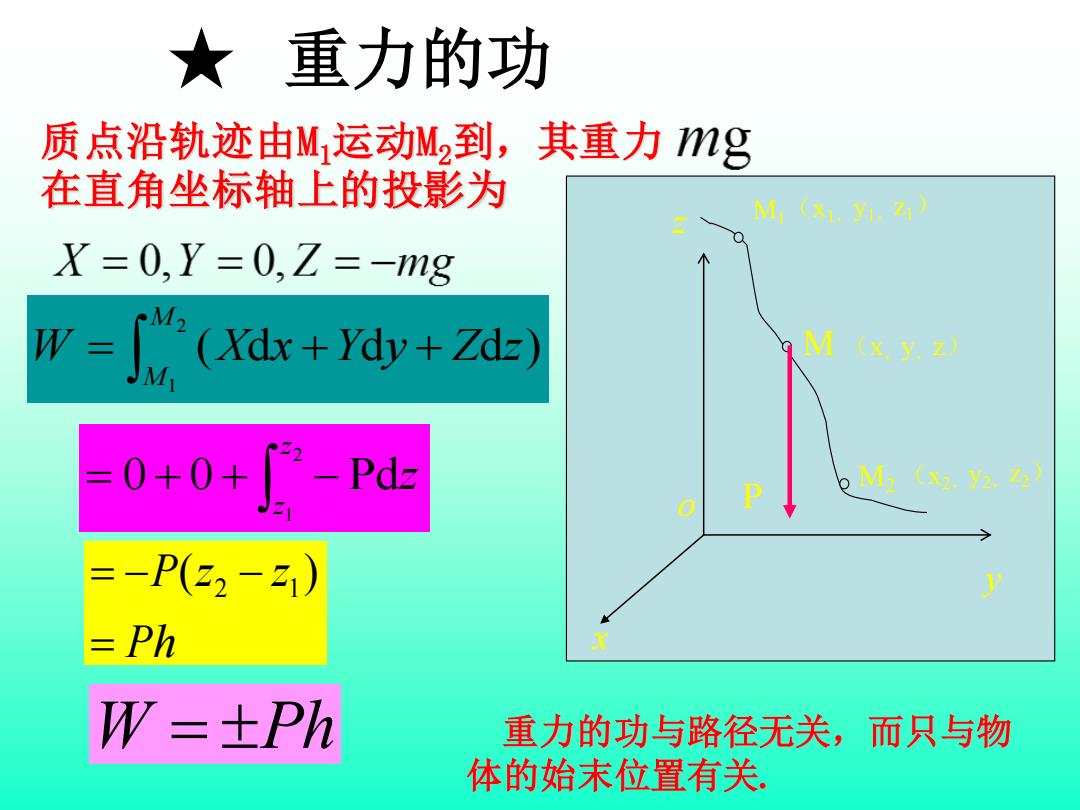
★重力的功 质点沿轨迹由M运动M2到,其重力mg 在直角坐标轴上的投影为 M1(81,y1,Z4) X=0,Y=0,Z=-mg W- (Xdx+Ydy+Zdz) M (x.y.z) =0+0+-Pd o M xz,y222】 0 =-P(2-1) Ph W=±Ph 重力的功与路径无关,而只与物 体的始末位置有关
( d d d ) 2 1 = + + M M W X x Y y Z z = + + − 2 1 0 0 Pd z z z Ph P z z = = − ( − ) 2 1 W = Ph 重力的功与路径无关,而只与物 体的始末位置有关. ★ 重力的功 质点沿轨迹由M1运动M2到,其重力 在直角坐标轴上的投影为 y o x z M (x,y,z) P