
Mac=∑F Maa=∑F Ma,=∑F 外力向一点简化:主矢 主矩 主矩对质系的运动有何影响呢?
外力向一点简化: 主矢 主矩 = e MaC Fi = e Macx Fx = e cy Ma Fy 主矩对质系的运动有何影响呢?
质点 动量定理: 质点系 动量的改变一→外力(外力系主矢) 若当质心为固定轴上一点时, v=0,则其动量恒等于零, 质心无运动,可是质点系确受外力 的作用 。 动量矩定理建立了质点和质点系相 对于某固定点(固定轴)的动量矩 的改变与外力对同一点(轴)之矩 两者之间的关系
质点 质点系 动量定理: 动量的改变—→外力(外力系主矢) C p = 0 若当质心为固定轴上一点时, vC=0,则其动量恒等于零, 质心无运动,可是质点系确受外力 的作用。 动量矩定理建立了质点和质点系相 对于某固定点(固定轴)的动量矩 的改变与外力对同一点(轴)之矩 两者之间的关系

爬绳比赛的力学分折 mA=mB Var VBr 谁最先到 达顶点
谁最先到 ?达顶点

动量矩守恒定理实例 直升机如果 没有尾翼将发生 什么现象 直升飞机尾桨的平衡作用
?直升飞机如果 没有尾翼将发生 什么现象

第12章质点系动量矩定理 口动量矩 D 口动量矩定理 D 口刚体定轴转动微分方程 D 口质点系相对质心的动量矩定理 ☒ 口刚体平面运动微分方程 口讨论 周
第12章 质点系动量矩定理 □ 动量矩定理 □ 刚体定轴转动微分方程 □ 讨论 □质点系相对质心的动量矩定理 □ 刚体平面运动微分方程 □ 动量矩
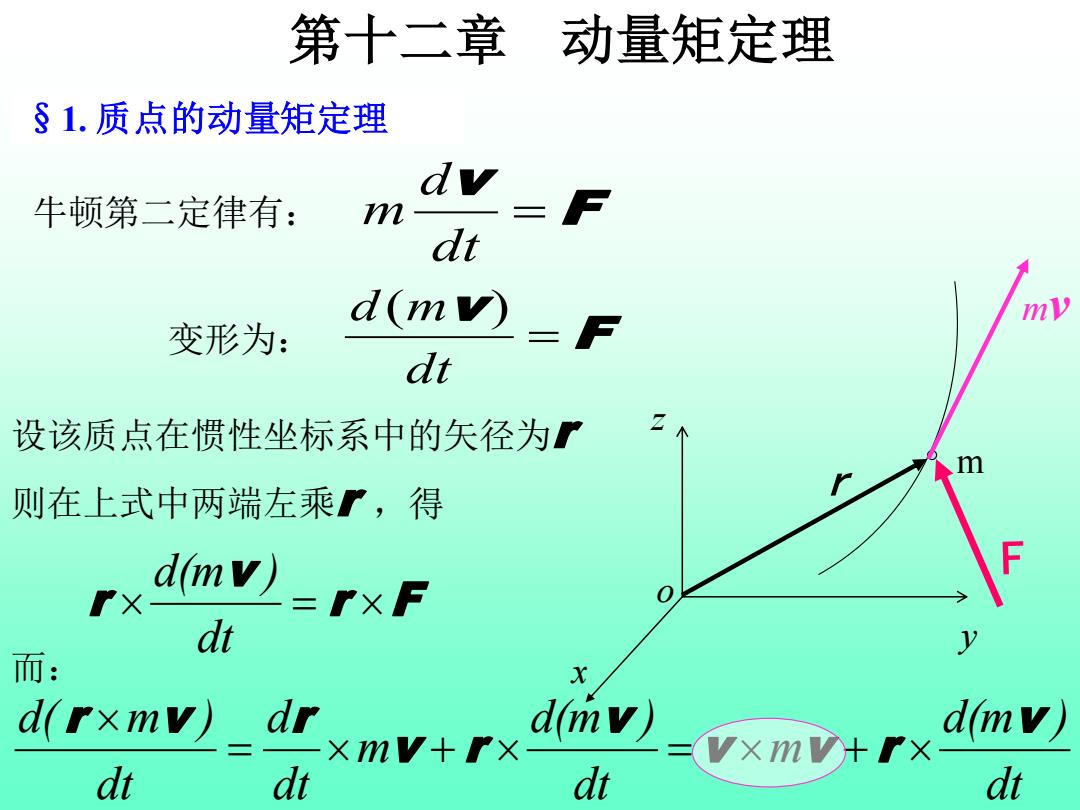
第十二章 动量矩定理 §1.质点的动量矩定理 dv 牛顿第二定律有: m F dt d(mv) =万 my 变形为: dt 设该质点在惯性坐标系中的矢径为『 则在上式中两端左乘了,得 X d(mv)=rxF dt 而: d(rxmv) dr d(mv) d(mv) xmV+r× VxmV+rX dt dt dt dt
第十二章 动量矩定理 §1. 质点的动量矩定理 m mv y o x z 牛顿第二定律有: F v = dt d m 设该质点在惯性坐标系中的矢径为r r F v r = dt d(m ) 而: dt d(m ) m dt d(m ) m dt d dt d( m ) v v v r v v r r v r = + = + F v = dt d(m ) 变形为: 则在上式中两端左乘r ,得

d(rxmv) dt 即:L,=m dt 即为质点的动量矩定理 其中: L。=r×mv 为质点的动量对固定点O的动量矩 m。=r×F为作用在质点上的合力F对固定,点O的力矩. 投影式为: dLx二mx dLy 二my 二m dt dt dt 若在运动过程中,作用在质点上的合力对固定点O的矩恒为0,则 该质点动量矩守恒: L0=常数 若在运动过程中,作用在质点上的合力对某固定轴的矩恒为0,则 该质点对该轴的动量矩守恒: L,=常数
r F r v = dt d( m ) 即为质点的动量矩定理. o o dt dL 即: = m 为作用在质点上的合力 F对固定点O的力矩. 为质点 对固定点O的动 ; m r F L r v = = o o m 的动量 量 矩 其中: 投影式为: z z y y x x m dt dL m dt dL m dt dL = = = 若在运动过程中,作用在质点上的合力对固定点O的矩恒为0,则 该质点动量矩守恒: L 0 =常数 若在运动过程中,作用在质点上的合力对某固定轴的矩恒为0,则 该质点对该轴的动量矩守恒: Lz = 常数

§2.质点系的动量矩定理 1、质系的动量矩 Lo=∑l。=∑(Ta×m,V:) 投影式 L.=Le=∑m(m,y) 2、转动刚体对转轴的动量矩 质点m对z轴的动量矩为: L2=m,y,=3m,0=m,0 整个刚体对z轴的动量矩为: L=∑.=∑m,ω=(②m,)@ 即,转动刚体对转轴的动量矩为: L=J⊙ 其中,J,=2mr 为刚体对转轴的转动惯量, 为一常数
§2. 质点系的动量矩定理 1、质系的动量矩 ( ) 0 i v i L r o mi = l = 投影式 L ΣL Σm (m v ) z = i z = z i i 2、转动刚体对转轴的动量矩 z ω 质点mi对z轴的动量矩为: 2 z i i i i i i i i l = rm v = rm r = m r 整个刚体对z轴的动量矩为: ( ) 2 2 z z i i i i L = l = m r = m r 即,转动刚体对转轴的动量矩为: Lz = Jz 其中, 为刚体对转轴的转动惯量, 为一常数. 2 i i = m r z J

§3.转动惯量、平移轴定理 J.=EmI 为刚体对转轴的转动惯量,为一常数, 同质量一样,转动惯量是刚体固有的物理属性,它与刚体的运 动无关,也不来自任何力学定理。一旦转轴确定,转动惯量即为恒 定,且恒为正值。 对于连续体 若把刚体的总质量M集中于刚体上某一点处,该点到转轴的距 离为p,则有: Jz =Mp P:回转半径或惯性半径 平移轴定理:J,=Jc+Md (证明从略) 刚体对任意轴的转动惯量J等于对与该轴平行的质心轴的转动 惯量Jc加上刚体的总质量与两轴间距离d的平方的乘积。 可见,刚体对质心轴的转动惯量最小
§3. 转动惯量、平移轴定理 为刚体对转轴的转动惯量,为一常数. 2 i i = m r z J 同质量一样,转动惯量是刚体固有的物理属性,它与刚体的运 动无关,也不来自任何力学定理。一旦转轴确定,转动惯量即为恒 定,且恒为正值。 对于连续体 J r dm M 2 Z = 若把刚体的总质量M集中于刚体上某一点处,该点到转轴的距 离为ρ,则有: 2 J Z = M 平移轴定理: 2 J Z = J C + Md 刚体对任意轴的转动惯量JZ等于对与该轴平行的质心轴的转动 惯量JC加上刚体的总质量与两轴间距离d的平方的乘积。 可见,刚体对质心轴的转动惯量最小。 (证明从略) ρ:回转半径或惯性半径
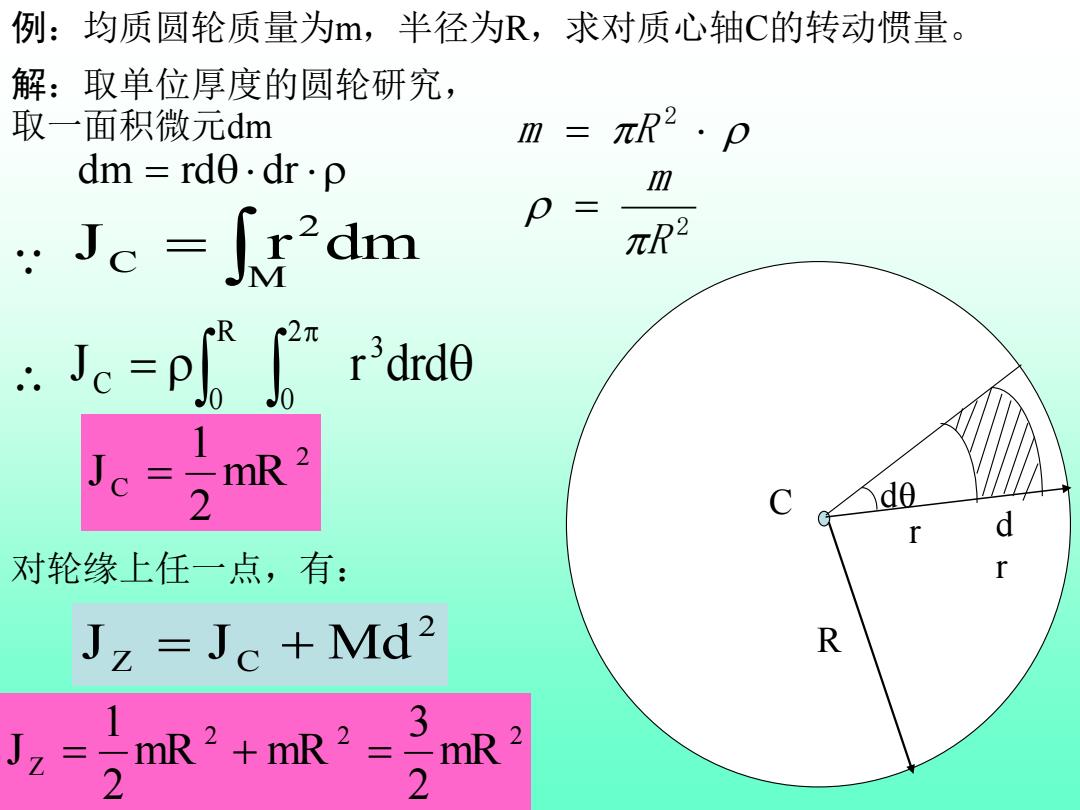
例:均质圆轮质量为,半径为R,求对质心轴C的转动惯量。 解:取单位厚度的圆轮研究, 取一面积微元dm m=πR2·p dm=rdo.dr·p m Je =y2dm p= 元R2 Jc-pp" 'drd0 Je mR 2 2 id0 r 对轮缘上任一点,有: Jz=Jc+Md2 R Jz=mR2+mR2=3mR 2 2
例:均质圆轮质量为m,半径为R,求对质心轴C的转动惯量。 C R dθ r d r 解:取单位厚度的圆轮研究, 取一面积微元dm dm = rd dr J r dm M 2 C = = 2 0 3 R 0 C J r drd 2 C mR 2 1 J = ∵ ∴ 对轮缘上任一点,有: 2 J Z = J C + Md 2 2 2 Z mR 2 3 mR mR 2 1 J = + = = 2 m R 2 R m =