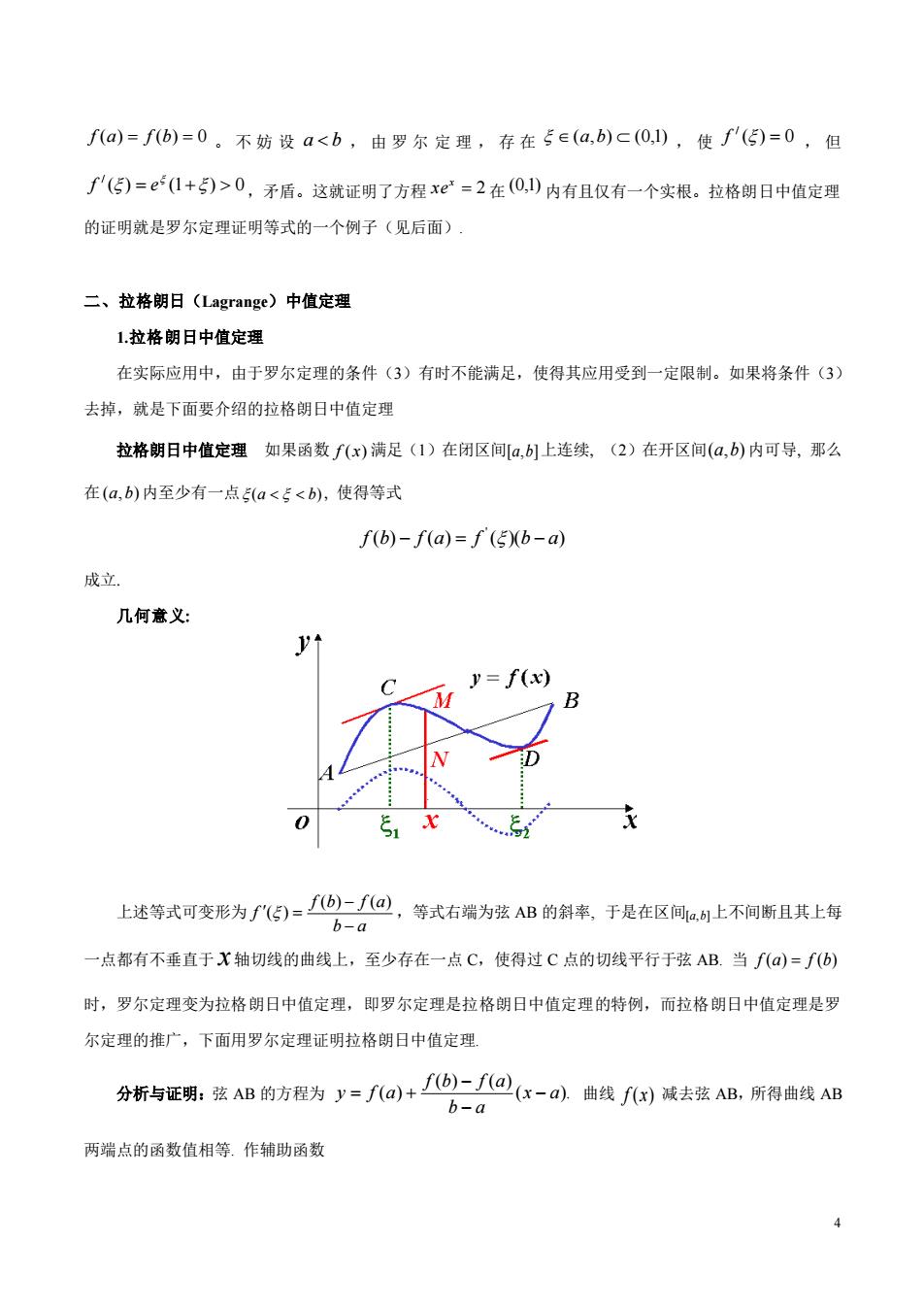
f(a)=f(b)=0。不妨设a<b,由罗尔定理，存在5∈(a,b)c(0,1),使f'()=0,但 '(⑤)=0+)>0，矛盾。这就证明了方程xe=2在(0，)内有且仅有一个实根。拉格朗日中值定理 的证明就是罗尔定理证明等式的一个例子（见后面） 二、拉格朗日(Lagrange)中值定理 1拉格朗日中值定理 在实际应用中，由于罗尔定理的条件(3)有时不能满足，使得其应用受到一定限制。如果将条件(3 去掉，就是下面要介绍的拉格朗日中值定理 拉格朗日中值定理如果函数fx)满足(1)在闭区间[a,1上连续，(2)在开区间(a,b)内可导，那么 在(a,b)内至少有一点a<E<b),使得等式 f(b)-f(a)=f'(5b-a) 成立 几何意义： f(x) 上述等式可变形为∫《们=⑥)-@，等式右端为弦AB的斜率，于是在区间止不间断且其上每 b-a 点都有不垂直于X轴切线的曲线上，至少存在一点C,使得过C点的切线平行于弦AB.当f()-f(b) 时，罗尔定理变为拉格朗日中值定理，即罗尔定理是拉格朗日中值定理的特例，而拉格朗日中值定理是罗 尔定理的推广，下面用罗尔定理证明拉格朗日中值定理 分析与证明：弦AB的方程为y=fa+-/@x-a)曲线f)减去弦AB,所得曲线AB 6-a 两端点的函数值相等.作辅助函数4 f (a) = f (b) = 0 。 不 妨 设 a  b ， 由 罗 尔 定 理 ， 存 在   (a,b)  (0,1) ， 使 ( ) 0 / f  = ， 但 ( ) (1 ) 0 /  = +   f e ，矛盾。这就证明了方程 = 2 x xe 在 (0,1) 内有且仅有一个实根。拉格朗日中值定理 的证明就是罗尔定理证明等式的一个例子（见后面）. 二、拉格朗日（Lagrange）中值定理 1.拉格朗日中值定理 在实际应用中，由于罗尔定理的条件（3）有时不能满足，使得其应用受到一定限制。如果将条件（3） 去掉，就是下面要介绍的拉格朗日中值定理 拉格朗日中值定理 如果函数 f (x) 满足（1）在闭区间 [a,b] 上连续 （2）在开区间 (a,b) 内可导 那么 在 (a,b) 内至少有一点  (a    b) 使得等式 ( ) ( ) ( )( ) ' f b − f a = f  b − a 成立 几何意义 上述等式可变形为 b a f b f a f − −  = ( ) ( ) ( ) ，等式右端为弦 AB 的斜率, 于是在区间 [a,b] 上不间断且其上每 一点都有不垂直于 x 轴切线的曲线上，至少存在一点 C，使得过 C 点的切线平行于弦 AB. 当 f (a) = f (b) 时，罗尔定理变为拉格朗日中值定理，即罗尔定理是拉格朗日中值定理的特例，而拉格朗日中值定理是罗 尔定理的推广，下面用罗尔定理证明拉格朗日中值定理. 分析与证明：弦 AB 的方程为 ( ). ( ) ( ) ( ) x a b a f b f a y f a − − − = + 曲线 f (x) 减去弦 AB，所得曲线 AB 两端点的函数值相等. 作辅助函数