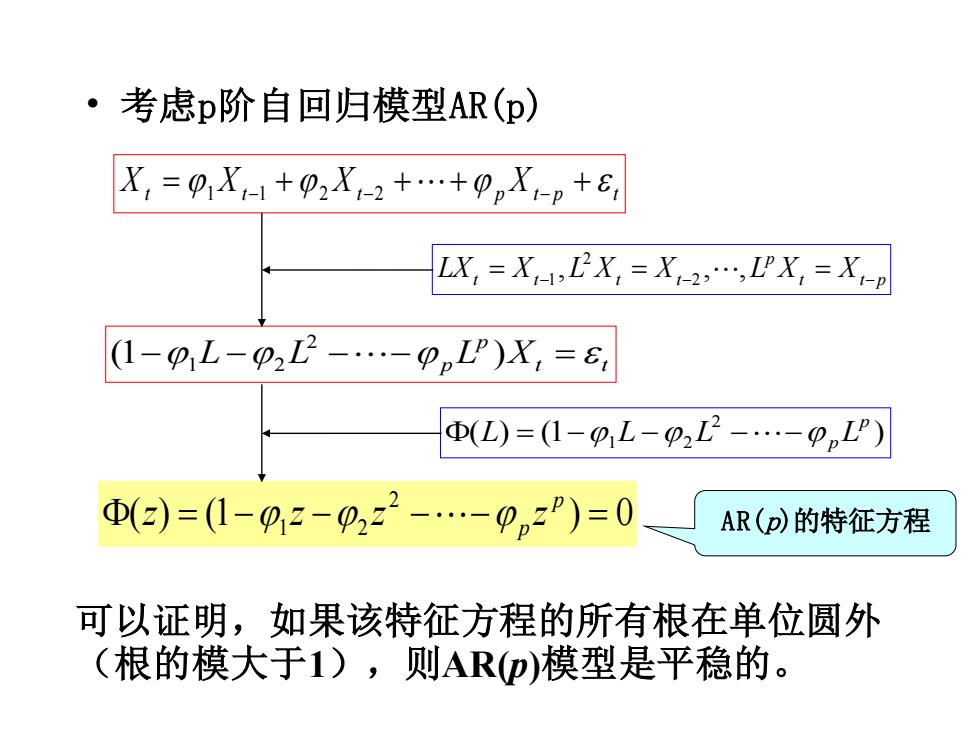
·考虑p阶自回归模型AR(p) X,=0X1+p2X1-2+.+9pX-p+6, LX =XLX =X2:,IPX=XP (1-pL-p2L2-ppL)X=6, D(L)=(1-p,L-p2L2-.-pL') 0(2）=(1-02-02z2-9nzP)=0 AR(D)的特征方程 可以证明，如果该特征方程的所有根在单位圆外 (根的模大于1)，则ARp)模型是平稳的。• 考虑p阶自回归模型AR(p) Xt Xt Xt p Xt p t =  + + + +  1 −1 2 −2  − t t p p LXt = Xt− L Xt = Xt− L X = X − , , , 2 2 1  t t p (1− L − L − − p L )X =  2 1 2  ( ) (1 ) 2 1 2 p  L = − L − L −− p L ( ) (1 ) 0 2  = − 1 − 2 − − = p p z  z  z   z AR(p)的特征方程 可以证明，如果该特征方程的所有根在单位圆外 （根的模大于1），则AR(p)模型是平稳的