
§8.2随机时间序列分析模型 Stochastic Time Serial Model 一、时间序列模型概述 二、随机时间序列模型的平稳性条件 三、随机时间序列模型的识别 四、随机时间序列模型的估计 五、随机时间序列模型的检验
§8.2 随机时间序列分析模型 Stochastic Time Serial Model 一、时间序列模型概述 二、随机时间序列模型的平稳性条件 三、随机时间序列模型的识别 四、随机时间序列模型的估计 五、随机时间序列模型的检验

说明 ·严格从理论体系讲,本节内容属于时间序列分 析,但不属于我们所定义的狭义的计量经济学。 。 本节内容一般不纳入计量经济学的课堂教学内 容,供没有学习过应用数理统计或者经济预测 课程的同学自学。 ·课件只提供一个简单的思路
说明 • 严格从理论体系讲,本节内容属于时间序列分 析,但不属于我们所定义的狭义的计量经济学。 • 本节内容一般不纳入计量经济学的课堂教学内 容,供没有学习过应用数理统计或者经济预测 课程的同学自学。 • 课件只提供一个简单的思路

一、时间序列模型概述
一、时间序列模型概述

1、时间序列模型 ·两类时间序列模型 - 时间序列结构模型:通过协整分析,建立反映不同时间 序列之间结构关系的模型,揭示了不同时间序列在每个 时点上都存在的结构关系。 一随机时间序列模型:揭示时间序列不同时点观测值之间 的关系,也称为无条件预测模型。 ·随机性时间序列模型包括:AR(p)、MA(q)、 ARMA(P,q)。 ·随机性时间序列模型并不属于现代计量经济学
1、时间序列模型 • 两类时间序列模型 – 时间序列结构模型:通过协整分析,建立反映不同时间 序列之间结构关系的模型,揭示了不同时间序列在每个 时点上都存在的结构关系。 – 随机时间序列模型:揭示时间序列不同时点观测值之间 的关系,也称为无条件预测模型。 • 随机性时间序列模型包括:AR(p)、MA(q)、 ARMA(p,q)。 • 随机性时间序列模型并不属于现代计量经济学

2、随机时间序列模型的适用性 ·用于无条件预测 、 结构模型用于预测的条件:建立正确的结构模型,给定 外生变量的预测值。 一无条件预测模型的优点。 ·结构模型的简化形式 一 结构模型经常可以通过约化和简化,变换为随及时间序 列模型
2、随机时间序列模型的适用性 • 用于无条件预测 – 结构模型用于预测的条件:建立正确的结构模型,给定 外生变量的预测值。 – 无条件预测模型的优点。 • 结构模型的简化形式 – 结构模型经常可以通过约化和简化,变换为随及时间序 列模型

二、随机时间序列模型的平稳性条件
二、随机时间序列模型的平稳性条件

1、AR(p)模型的平稳性条件 随机时间序列模型的平稳性,可通过它所生成 的随机时间序列的平稳性来判断。 。1 如果一个p阶自回归模型AR(p)生成的时间序列 是平稳的,就说该AR(p)模型是平稳的; 否则,就说该AR(p)模型是非平稳的
1、AR(p)模型的平稳性条件 • 随机时间序列模型的平稳性,可通过它所生成 的随机时间序列的平稳性来判断。 • 如果一个p阶自回归模型AR(p)生成的时间序列 是 平 稳 的 , 就说该 AR(p) 模 型 是 平 稳 的 ; 否则,就说该AR(p)模型是非平稳的
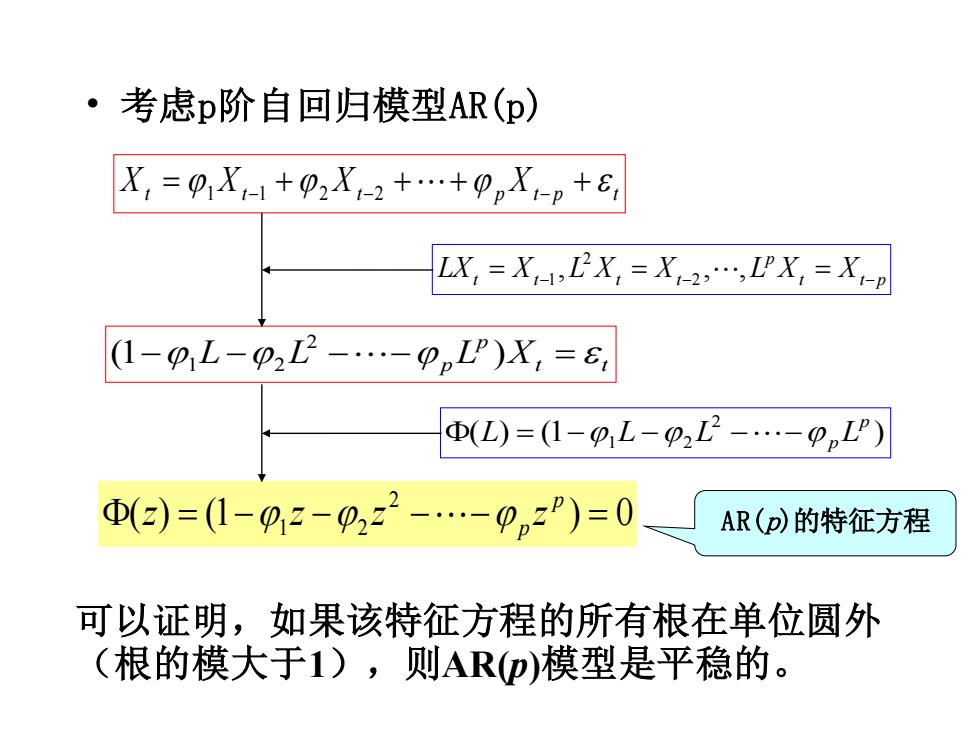
·考虑p阶自回归模型AR(p) X,=0X1+p2X1-2+.+9pX-p+6, LX =XLX =X2:,IPX=XP (1-pL-p2L2-ppL)X=6, D(L)=(1-p,L-p2L2-.-pL') 0(2)=(1-02-02z2-9nzP)=0 AR(D)的特征方程 可以证明,如果该特征方程的所有根在单位圆外 (根的模大于1),则ARp)模型是平稳的
• 考虑p阶自回归模型AR(p) Xt Xt Xt p Xt p t = + + + + 1 −1 2 −2 − t t p p LXt = Xt− L Xt = Xt− L X = X − , , , 2 2 1 t t p (1− L − L − − p L )X = 2 1 2 ( ) (1 ) 2 1 2 p L = − L − L −− p L ( ) (1 ) 0 2 = − 1 − 2 − − = p p z z z z AR(p)的特征方程 可以证明,如果该特征方程的所有根在单位圆外 (根的模大于1),则AR(p)模型是平稳的

容易得到如下平稳性条件 X:=0X-1+8 lo<1 X,=p1X,-1+p2X,-2+8, p+02<1,9-p2<1,p2<1 X:=0X1+02X2+.+opX-p+E 01+02++pp<1 0,|+|p2++|9pK1
容易得到如下平稳性条件 Xt = Xt−1 + t 1 Xt Xt Xt t = + + 1 −1 2 −2 1 +2 1,1 −2 1, 2 1 1 1 + 2 ++ p | | | | | | 1 1 + 2 ++ p Xt Xt Xt p Xt p t = + + + + 1 −1 2 −2 −

2、MA(q)模型的平稳性 X,=6,-06-8g6-g E(X,)=E(c,)-0,E(G,-)-0,E(e,-g)=0 Y。=/ar(X,)=(1+0+.+0g)82 %=CoX,X-i)=(-0+0,02+0,03+.+0,-10,)62 Yg-=C0(X1,X,-g+1)=(-0-1+0,0,)62 当滞后期大于q Yg=Co(X,X,-g)=-0,δ2 时,X的自协方 差系数为0。 ·有限阶移动平均模型总是平稳的
2、MA(q)模型的平稳性 • 有限阶移动平均模型总是平稳的。 Xt = t − t− − − q t−q 1 1 ( ) ( ) ( ) ( ) 0 E Xt = E t −1 E t−1 −− q E t−q = ( ) 2 2 1 1 1 1 2 1 1 1 1 2 2 3 1 2 2 2 0 1 ( , ) ( , ) ( ) ( , ) ( ) (1 ) q t t q q q t t q q q t t q q t q Cov X X Cov X X Cov X X Var X = = − = = − + = = − + + + + = = + + + − − − + − − − 当滞后期大于q 时,X的自协方 差系数为0