《计量经济学》课程教学资源（PPT课件）课程PPT教学课件（第3版）第三章 经典单方程计量经济学模型（多元线性回归模型）Multiple Linear Regression Model

第三章经典单方程计量经济学模型：多 元线性回归模型 Multiple linear regression Model

第三章 经典单方程计量经济学模型：多 元线性回归模型 Multiple Linear Regression Model

说明 ·考虑到一些学校将一元回归模型作为自学内容 ,直接从多元回归模型开始讲授，所以本章课 件有一部分内容与第2章重复。（主要出现在 基本假设和估计方法部分) 。 如果从一元回归模型开始讲授，可以将本章课 件的重复内容略去

说明 • 考虑到一些学校将一元回归模型作为自学内容 ，直接从多元回归模型开始讲授，所以本章课 件有一部分内容与第2章重复。（主要出现在 基本假设和估计方法部分） • 如果从一元回归模型开始讲授，可以将本章课 件的重复内容略去

本章内容 ·多元线性回归模型概述 ·多元线性回归模型的参数估计 ·多元线性回归模型的统计检验 ·多元线性回归模型的预测 可化为线性的非线性模型 受约束回归

本章内容 • 多元线性回归模型概述 • 多元线性回归模型的参数估计 • 多元线性回归模型的统计检验 • 多元线性回归模型的预测 • 可化为线性的非线性模型 • 受约束回归

§3.1多元线性回归模型概述 (Regression Analysis) 一、多元线性回归模型 二、多元线性回归模型的基本假设

§3.1 多元线性回归模型概述 (Regression Analysis) 一、多元线性回归模型 二、多元线性回归模型的基本假设

一、多元线性回归模型

一、多元线性回归模型

总体回归模型 ·总体回归模型：总体回归函数的随机表达形式 Y:=B+B1X:+B2X2,+.+B4Xa+4, =1,2.,n 为解释变量的数目。习惯上，把常数项看成 为虚变量的系数，该虚变量的样本观测值始终 取1。于是，模型中解释变量的数目为（k+1)。 B;称为回归参数（regression coefficient)

总体回归模型 Yi   X i  X i +  k X ki +  i = + + +    0 1 1 2 2 i=1,2.,n • 总体回归模型：总体回归函数的随机表达形式 k为解释变量的数目。习惯上，把常数项看成 为虚变量的系数，该虚变量的样本观测值始终 取1。于是，模型中解释变量的数目为（k+1）。  j称为回归参数（regression coefficient）

总体回归函数 ·总体回归函数：描述在给定解释变量X条件下 被解释变量Y的条件均值。 E(YX X2Xg)=Bo+BX+BX2++BXg B,也被称为偏回归系数(partial regression coefficients),表示在其他解释变量保持不变 的情况下，X每变化1个单位时，Y的均值 E(Y)的变化。 或者说B给出了X的单位变化对Y均值的 “直接”或“净”（不含其他变量）影响

• 总体回归函数：描述在给定解释变量Xi条件下 被解释变量Yi的条件均值。 E Yi X i X i Xki   X i  X i +  k Xki = + + + 1 2 0 1 1 2 2 ( | , ,  ) j也被称为偏回归系数(partial regression coefficients)，表示在其他解释变量保持不变 的情况下，Xj每变化1个单位时，Y的均值 E(Y)的变化。 或者说j给出了Xj的单位变化对Y均值的 “直接”或“净”（不含其他变量）影响。 总体回归函数

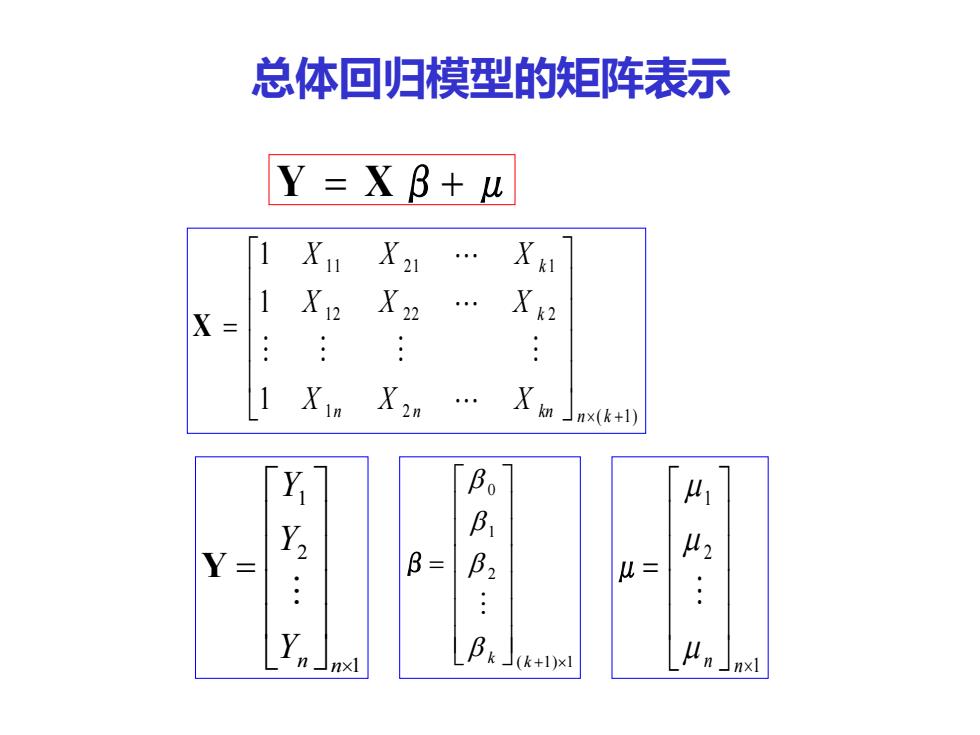
总体回归模型的矩阵表示 Y=XB+u 1 XI 1 X= X 12 X k2 Xin X2n Xa]nxk+山 Bo 4 B Y- B= B2 H : ☐nxl 阝k]k+x刘 nxl

总体回归模型的矩阵表示 Y = Xβ+ μ ( 1) 1 2 1 2 2 2 2 1 1 2 1 1 1 1 1  +             = n k n n kn k k X X X X X X X X X        X 1 2 1              = n n Y Y Y  Y ( 1) 1 2 1 0 +                  = k  k     β 1 2 1              = n  n    μ

样本回归函数与样本回归模型 从一次抽样中获得的总体回归函数的近似，称为样 本回归函数(sample regression function)。 ·样本回归函数的随机形式，称为样本回归模型 (sample regression model) 。 ,=B。+BX.+B2X2,+.+BaXa y,=B。+BXz+B2X2+.+BaXa+e

样本回归函数与样本回归模型 • 从一次抽样中获得的总体回归函数的近似，称为样 本回归函数（sample regression function）。 • 样本回归函数的随机形式，称为样本回归模型 （sample regression model）。 Yi   X i  X i  ki Xki ˆ ˆ ˆ ˆ ˆ = 0 + 1 1 + 2 2 ++ i i i ki ki i Y =  +  X +  X + +  X + e ˆ ˆ ˆ ˆ 0 1 1 2 2 

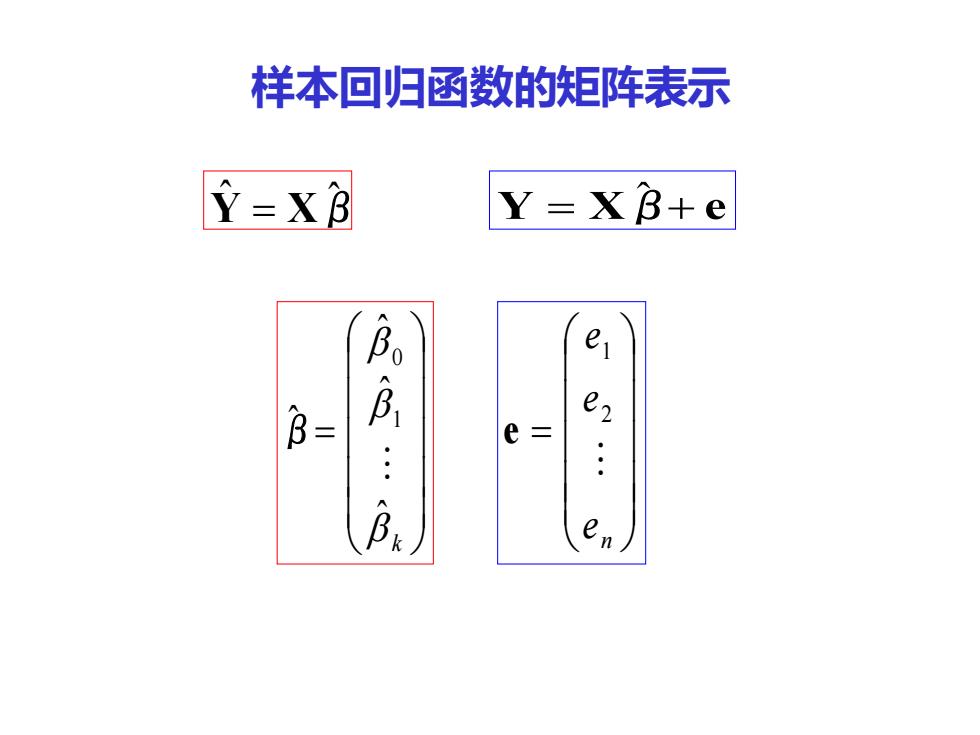
样本回归函数的矩阵表示 Y=xB Y=XB+e 'b e B= B e2 e= B】 en

样本回归函数的矩阵表示 Y ˆ = Xβ ˆ Y = Xβ ˆ + e               =  k   ˆ ˆ ˆ ˆ 1 0  β               = n e e e  2 1 e