
第三章多元孩性回归模型 PDF文件使用"pdfFactory Pro”试用版本创建wm,fineprint.cL
第三章 多元线性回归模型 PDF 文件使用 "pdfFactory Pro" 试用版本创建 @www.fineprint.cn

目录 第一节、多元线性回归模型 第二节、多元线性回归模型的参数估计 •第三节、多元线性回归模型的统计检验 第四节、多元线性回归模型的预测 第五节、回归模型的其他形式 PDF文件使用"pdfFactory Pro”试用版本创建ww,fineprint.cn
•第一节、多元线性回归模型 •第二节、多元线性回归模型的参数估计 •第三节、多元线性回归模型的统计检验 •第四节、多元线性回归模型的预测 •第五节、回归模型的其他形式 目录 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

第一节:多元线性回归模型 一、多元线性回归模型 二、多元线性回归模型的基本假定 PDF文件使用"pdfFactory Pro”试用版本创建wm,fineprint.cL
第一节:多元线性回归模型 一、多元线性回归模型 二、多元线性回归模型的基本假定 PDF 文件使用 "pdfFactory Pro" 试用版本创建 ÿwww.fineprint.cn

一、多元线性回归模型 多元线性回归模型:表现在线性回归模型中的 解释变量有多个。 一般表现形式: Y=B+BX+B2X+.+BX+4i =1,2n 其中:k为解释变量的数目,B称为回归参数 (regression coefficient). 习惯上:把常数项看成为一虚变量的系数,该 虚变量的样本观测值始终取1。 此式也被称为总体回归函数的随机表达形 式 PDF文件使用"pdfFactory Pro”试用版本创建mm,fineprint.c四
多元线性回归模型:表现在线性回归模型中的 解释变量有多个。 一般表现形式: Yi b b X i b X i +bkXki +mi = + + +××× 0 1 1 2 2 i=1,2.,n 其中:k为解释变量的数目,bj称为回归参数 (regression coefficient)。 习惯上:把常数项看成为一虚变量的系数,该 虚变量的样本观测值始终取1。 此式也被称为总体回归函数的随机表达形 式 一、多元线性回归模型 PDF 文件使用 "pdfFactory Pro" 试用版本创建 ÿwww.fineprint.cn

一、多元线性回归模型 非随机表达式为: EYIX,X,ΛXa)=B+βX+E2X2,++BX 方程表示:各变量X值固定时Y的平均响应。 B也被称为偏回归系数,表示在其他解释变 量保持不变的情况下,X每变化1个单位时,Y 的均值E(Y)的变化; 或者说B,给出了X的单位变化对Y均值的“直 接”或“净”影响。 PDF文件使用"pdfFactory Pro”试用版本创建wm,fineprint.cL
非随机表达式为: E Yi X i X i Xki b b X i b X i +bkXki = + + +××× 1 2 0 1 1 2 2 ( | , ,L ) 方程表示:各变量X值固定时Y的平均响应。 bj也被称为偏回归系数,表示在其他解释变 量保持不变的情况下,Xj每变化1个单位时,Y 的均值E(Y)的变化; 或者说bj给出了Xj的单位变化对Y均值的“直 接”或“净”影响。 一、多元线性回归模型 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

多元线性回归模型 总体回归模型个随机方程的矩阵表达式为 B。 h . 1 B M MM M M Y M B u Y=X +U PDF文件使用"pdfFactory Pro”试用版本创建ww,fineprint.cn
÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ + ÷ ÷ ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç ç ç è æ ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ = ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ u u u X X X X X X X X X Y Y Y n k kn k k n n n M M M L L L M M M M 2 1 2 1 0 2 1 2 22 21 1 12 11 2 1 1 1 1 b b b b Y = Xb +U 一、多元线性回归模型 总体回归模型n个随机方程的矩阵表达式为 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn
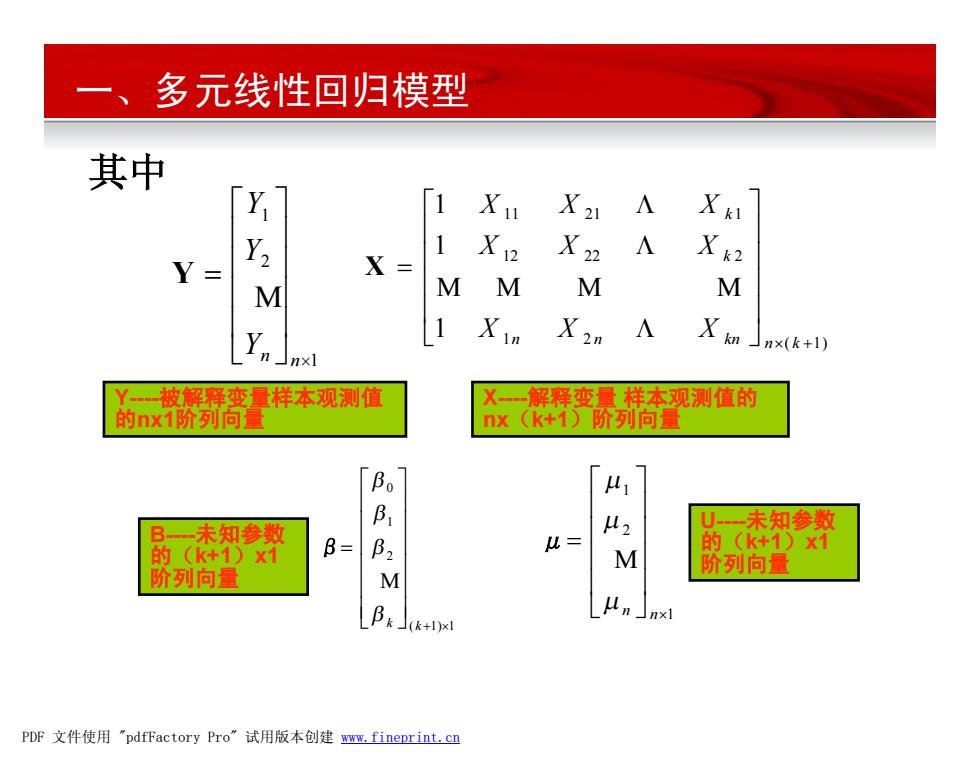
一、多元线性回归模型 其中 Y Xn X21 X k 1 X= X12 X22 Y X k2 M M M M M X2n kn n×(k+1) nxl Y~被解释变量样本观测值 X一解释变量样本观测值的 的nx1阶列向量 nx(k+1)阶列向量 Bo 1 U一末未知参数 B一未知参数 的(k+1)x1 的kK+1)X1 B= 月VM 阶列向量 阶列向量 阝k」(k+ PDF文件使用"pdfFactory Pro”试用版本创建wm,fineprint.cn
其中 1 2 ( 1) 12 22 2 11 21 1 1 1 1 ´ + ú ú ú ú û ù ê ê ê ê ë é = n k n n kn k k X X X X X X X X X L M M M M L L X ( 1) 1 2 1 0 + ´ ú ú ú ú ú ú û ù ê ê ê ê ê ê ë é = k b k b b b M β 1 2 1 ´ ú ú ú ú û ù ê ê ê ê ë é = n n m m m M μ 一、多元线性回归模型 1 2 1 ´ ú ú ú ú û ù ê ê ê ê ë é = n n Y Y Y M Y Y-被解释变量样本观测值 的nx1阶列向量 X-解释变量 样本观测值的 nx(k+1)阶列向量 B-未知参数 的(k+1)x1 阶列向量 U-未知参数 的(k+1)x1 阶列向量 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

多元线性回归模型 样本回归函数:用来估计总体回归函数 ,=B。+BX,+B2X2:+Λ+BaX 其随机表示式: Y,=B。+βXu+B2X21+A+BXa+e 样本回归函数的矩阵表达: Y=XB 或 Y=XB+e 其中: 氵= B= M 房房M e= M PDF文件使用"pdfFactory Pro”试用版本创建ww,fineprint.cn
样本回归函数:用来估计总体回归函数 Yi b b X i b X i bki X ki ˆ ˆ ˆ ˆ ˆ = 0 + 1 1 + 2 2 +L + 其随机表示式: i i i ki ki i Y = b + b X + b X + + b X + e ˆ ˆ ˆ ˆ 0 1 1 2 2 L 样本回归函数的矩阵表达: Yˆ = Xβˆ 或 Y = Xβ+ e ˆ 其中: ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ = bk b b ˆ ˆ ˆ ˆ 1 0 M β ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ = n e e e M 2 1 e 一、多元线性回归模型 ÷ ÷ ÷ ÷ ÷ ø ö ç ç ç ç ç è æ = Y Y Y n Y ˆ ˆ ˆ 2 1 ˆ M PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

二、多元线性回归模型的基本假定 假设1、解释变量是非随机的或固定的,且各X之间 互不相关(无多重共线性)。 假设2、随机误差项具有零均值、同方差及不序列 相关性 E(4)=0 Var(u,)=E(42)=o2 Cov(41,4,)=E(4,4,)=0 i≠ji,j=1,2,Λ,n 假设3,解释变量与随机项不相关 Co(Xi,4,)=0 j=1,2A,k 假设4,随机项满足正态分布 4,~N(0,o2) PDF文件使用"pdfFactory Pro”试用版本创建wm,fineprint.cn
( ) = 0 E mi 2 2 Var(mi ) = E(mi ) = s ( , ) = ( ) = 0 Cov mi m j E mim j i ¹ j i, j = 1,2,L ,n 假设3,解释变量与随机项不相关 ( , ) = 0 C X ji i ov m 假设4,随机项满足正态分布 ~ (0, ) 2 mi N s j = 1,2L , k 二、多元线性回归模型的基本假定 假设1、解释变量是非随机的或固定的,且各X之间 互不相关(无多重共线性)。 假设2、随机误差项具有零均值、同方差及不序列 相关性 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

第二节、多元线性回归模型的参数估计 一、普通最小二乘估计 二、参数估计量的性质 三、样本容量问题 四、估计实例 PDF文件使用"pdfFactory Pro”试用版本创建ww,fineprint.cn
一 、普通最小二乘估计 二、参数估计量的性质 三、样本容量问题 四、估计实例 第二节、多元线性回归模型的参数估计 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn