
§3.2协整与误差修正模型 Cointegration and Error Correction Model 一、 长期均衡与协整分析 二、 协整检验 三、误差修正模型
§3.2 协整与误差修正模型 Cointegration and Error Correction Model 一、长期均衡与协整分析 二、协整检验 三、误差修正模型

一、长期均衡与协整分析 Equilibrium and Cointegration
一、长期均衡与协整分析 Equilibrium and Cointegration

1、问题的提出 ·经典回归模型(classical regression model)是建立在 平稳数据变量基础上的,对于非平稳变量,不能使用经典 回归模型,否则会出现虚假回归等诸多问题。 ·由于许多经济变量是非平稳的,这就给经典的回归分析方 法带来了很大限制。 ·但是,如果变量之间有着长期的稳定关系,即它们之间是 协整的(cointegration),则是可以使用经典回归模型方 法建立回归模型的。 ·例如,中国居民人均消费水平与人均GDP变量的例子,从 经济理论上说,人均GDP决定着居民人均消费水平,它们 之间有着长期的稳定关系,即它们之间是协整的
1、问题的提出 • 经典回归模型(classical regression model)是建立在 平稳数据变量基础上的,对于非平稳变量,不能使用经典 回归模型,否则会出现虚假回归等诸多问题。 • 由于许多经济变量是非平稳的,这就给经典的回归分析方 法带来了很大限制。 • 但是,如果变量之间有着长期的稳定关系,即它们之间是 协整的(cointegration),则是可以使用经典回归模型方 法建立回归模型的。 • 例如,中国居民人均消费水平与人均GDP变量的例子, 从 经济理论上说,人均GDP决定着居民人均消费水平,它们 之间有着长期的稳定关系,即它们之间是协整的

2、长期均衡; ·经济理论指出,某些经济变量间确实存在着长期均衡关 系,这种均衡关系意味着经济系统不存在破坏均衡的内在 机制,如果变量在某时期受到干疣后偏离其长期均衡点, 则测均衡机制将会在下一期进行调整以使其重新回到均衡状 。 假设X与Y间的长期“均衡关系”由式描述 Y,=00+01X,+4 该均衡关系意味着:给定X的一个值,Y相应的均衡值也随 之确定为0u,+01X
• 经济理论指出,某些经济变量间确实存在着长期均衡关 系,这种均衡关系意味着经济系统不存在破坏均衡的内在 机制,如果变量在某时期受到干扰后偏离其长期均衡点, 则均衡机制将会在下一期进行调整以使其重新回到均衡状 态。 假设X与Y间的长期“均衡关系”由式描述 2、长期均衡 Yt =0 +1 Xt + t 该均衡关系意味着:给定X的一个值,Y相应的均衡值也随 之确定为 0+1X

·在t-1期末,存在下述三种情形之一: -Y等于它的均衡值:YFo+o1X; -Y小于它的均衡值:Y1o+X; ·在时期t,假设X有一个变化量△X,如果变量X 与Y在时期与t-1末期仍满足它们间的长期均衡关 系,即上述第一种情况,则Y的相应变化量为: △Y,=△X,+, Vi-ut-ut-1
• 在t-1期末,存在下述三种情形之一: – Y等于它的均衡值:Yt-1= 0+1Xt; – Y小于它的均衡值:Yt-1 0+1Xt; • 在时期t,假设X有一个变化量Xt,如果变量X 与Y在时期t与t-1末期仍满足它们间的长期均衡关 系,即上述第一种情况,则Y的相应变化量为: t t t Y = X + v 1 vt =t-t-1

。1 如果t-1期末,发生了上述第二种情况,即Y的 值小于其均衡值,则期末Y的变化往往会比第 一种情形下Y的变化大一些; ● 反之,如果t-1期末Y的值大于其均衡值,则期 末Y的变化往往会小于第一种情形下的△Yt。 ·可见,如果Yoo+o1X+Ht正确地提示了X与Y 间的长期稳定的“均衡关系”,则意味着Y对 其均衡点的偏离从本质上说是“临时性”的。 一个重要的假设就是:随机扰动项必须是平稳 序列。如果有随机性趋势(上升或下降) 则会导致Y对其均衡点的任何偏离都会被长期 累积下来而不能被消除
• 如果t-1期末,发生了上述第二种情况,即Y的 值小于其均衡值,则t期末Y的变化往往会比第 一种情形下Y的变化大一些; • 反之,如果t-1期末Y的值大于其均衡值,则t期 末Y的变化往往会小于第一种情形下的Yt。 • 可见,如果Yt =0+1Xt+t正确地提示了X与Y 间的长期稳定的“均衡关系” ,则意味着Y对 其均衡点的偏离从本质上说是“临时性”的。 • 一个重要的假设就是:随机扰动项t必须是平稳 序列。如果t有随机性趋势(上升或下降), 则会导致Y对其均衡点的任何偏离都会被长期 累积下来而不能被消除

式Yo+oX+u中的随机扰动项也被称为非均 衡误差(disequilibrium error),它是变量X 与Y的一个线性组合: 4,=Y-a0-CX, ·如果X与Y间的长期均衡关系正确,该式表述的非 均衡误差应是一平稳时间序列,并且具有零期望值, 即是具有0均值的(0)序列。 ·非稳定的时间序列,它们的线性组合也可能成为 平稳的。称变量X与Y是协整的(cointegrated)
• 式Yt =0+1Xt+t中的随机扰动项也被称为非均 衡误差(disequilibrium error),它是变量X 与Y的一个线性组合: t = Yt −0 −1 Xt • 如果X与Y间的长期均衡关系正确,该式表述的非 均衡误差应是一平稳时间序列,并且具有零期望值, 即是具有0均值的I(0)序列。 • 非稳定的时间序列,它们的线性组合也可能成为 平稳的。称变量X与Y是协整的(cointegrated)

3、协整 ·如果序列{X1t,X2t,Xkt}都是d阶单整,存在向量 0=(c1,2,k),使得Z=0XT、I(d-b) 其中,b>0,X=(X1t,X2t,Xk)T,则认为序列 {X1t,X2t,Xkt}是(d,b)阶协整,记为XCI(d,b), a为协整向量(cointegrated vector)。 ·如果两个变量都是单整变量,只有当它们的单整 阶数相同时,才可能协整:如果它们的单整阶数 不相同,就不可能协整
3、协整 • 如果序列{X1t,X2t,.,Xkt}都是d阶单整,存在向量 =(1,2,.,k),使得Zt =X T ~ I(d-b), 其中,b>0,X=(X1t,X2t,.,Xkt) T,则认为序列 {X1t,X2t,.,Xkt}是(d,b)阶协整,记为Xt~CI(d,b), 为协整向量(cointegrated vector)。 • 如果两个变量都是单整变量,只有当它们的单整 阶数相同时,才可能协整;如果它们的单整阶数 不相同,就不可能协整
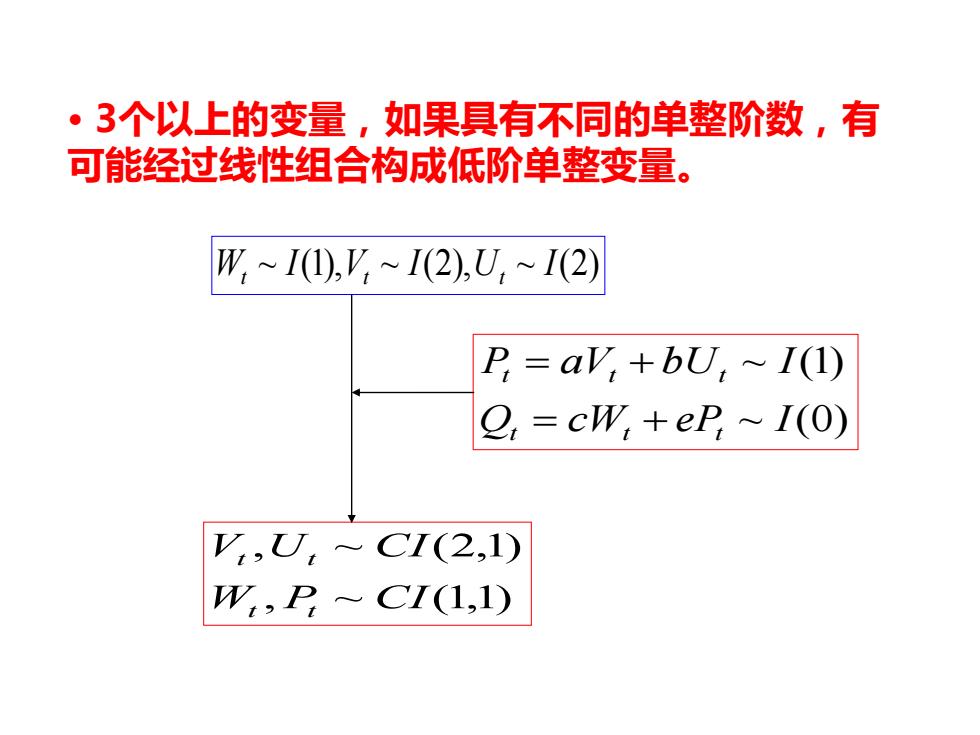
·3个以上的变量,如果具有不同的单整阶数,有 可能经过线性组合构成低阶单整变量。 W,~I(I),V~I(2),U,~1I(2) P=av,+bU ~I(1) 2,=cW,+eP~I(0) V,U,~CI(2,1) W,P~CI(1,1)
• 3个以上的变量,如果具有不同的单整阶数,有 可能经过线性组合构成低阶单整变量。 W ~ I(1),V ~ I(2),U ~ I(2) t t t ~ (0) ~ (1) Q cW eP I P aV bU I t t t t t t = + = + , ~ (1,1) , ~ (2,1) W P CI V U CI t t t t

(d,d)阶协整是一类非常重要的协整关系, 它的经济意义在于:两个变量,虽然它们具有 各自的长期波动规律,但是如果它们是(d,d) 阶协整的,则它们之间存在着一个长期稳定的 比例关系。 例如,中国CPC和GDPPC,它们各自都是2阶单整,如果 它们是(2,2)阶协整,说明它们之间存在着一个长期稳 定的比例关系,从计量经济学模型的意义上讲,建立 如下居民人均消费函数模型是合理的。 CPC do+a GDPPC+ ·尽管两个时间序列是非平稳的,也可以用经典 的回归分析方法建立回归模型
• (d,d)阶协整是一类非常重要的协整关系, 它的经济意义在于:两个变量,虽然它们具有 各自的长期波动规律,但是如果它们是(d,d) 阶协整的,则它们之间存在着一个长期稳定的 比例关系。 • 例如,中国CPC和GDPPC,它们各自都是2阶单整,如果 它们是(2,2)阶协整,说明它们之间存在着一个长期稳 定的比例关系,从计量经济学模型的意义上讲,建立 如下居民人均消费函数模型是合理的。 CPCt =0 +1 GDPPCt + t • 尽管两个时间序列是非平稳的,也可以用经典 的回归分析方法建立回归模型