
§9.3计量经济学应用模型函数关系设定 一、模型的关系类型 二、模型关系误设的后果 三、模型关系设定的指导原则 四、模型关系设定检验 五、案例一以要素替代性质描述为线 索的生产函数模型的发展
§9.3 计量经济学应用模型函数关系设定 一、模型的关系类型 二、模型关系误设的后果 三、模型关系设定的指导原则 四、模型关系设定检验 五、案例——以要素替代性质描述为线 索的生产函数模型的发展

一、模型的关系类型
一、模型的关系类型
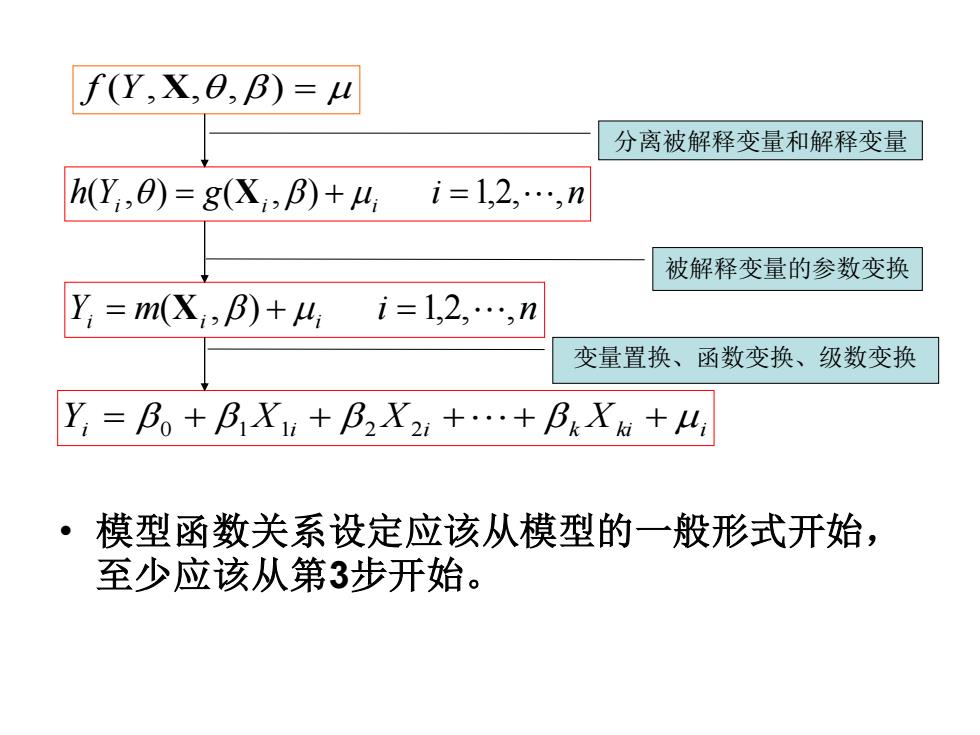
f(Y,X,0,B)=u 分离被解释变量和解释变量 h(Y,0)=g(X,B)+4i=1,2,.,n 被解释变量的参数变换 Y=mX,β)+4,i=1,2,.,n 变量置换、函数变换、级数变换 Y,=B。+B1Xi+B2X2:+.+BkX+4 ·模型函数关系设定应该从模型的一般形式开始, 至少应该从第3步开始
• 模型函数关系设定应该从模型的一般形式开始, 至少应该从第3步开始。 f (Y,X,, ) = h Y g i n i i i ( ,) = (X ,) + =1,2, , Y m i n i i i = (X ,) + =1,2, , Yi X i X i + k Xki + i = + + + 0 1 1 2 2 分离被解释变量和解释变量 被解释变量的参数变换 变量置换、函数变换、级数变换

二、模型关系误设的后果
二、模型关系误设的后果

1。“源生的”随机扰动项 ·随机项仅仅包括无数不显著因素对被解释变量的 影响。 ·客观存在。 ·由大数定理保证其满足Gauss假设,由中心极限 定理可以证明其服从正态分布。于是,建立在 Gauss假设和正态分布假设基础上的统计推断具 有可靠性
1. “源生的”随机扰动项 • 随机项仅仅包括无数不显著因素对被解释变量的 影响。 • 客观存在。 • 由大数定理保证其满足Gauss假设,由中心极限 定理可以证明其服从正态分布。于是,建立在 Gauss假设和正态分布假设基础上的统计推断具 有可靠性

2。“衍生的”随机误差项 ·随机项在“无数非显著因素对被解释变量的影响” 之外,加上诸如“变量观测值的观测误差的影 响”、“模型关系的设定误差的影响”等。 ·建模中衍生形成。 ·“源生的”随机扰动项所满足的极限法测是否适 用于“衍生”的随机误差项?Gauss假设和正态 分布假设是否仍然成立?
2. “衍生的”随机误差项 • 随机项在“无数非显著因素对被解释变量的影响” 之外,加上诸如“变量观测值的观测误差的影 响”、“模型关系的设定误差的影响”等。 • 建模中衍生形成。 • “源生的”随机扰动项所满足的极限法则是否适 用于“衍生”的随机误差项?Gauss假设和正态 分布假设是否仍然成立?

·正态性假设的违背: 一当存在模型关系误差时,如果解释变量是随机的,随 机误差项的正态性将得不到保证。 一当模型遗漏了显著的变量,如果遗漏的变量是非正态 的随机变量,随机误差项将不具有正态性。 一如果待估计的模型是原模型经过函数变换得到的,随 机误差项将不再服从正态分布
• 正态性假设的违背: – 当存在模型关系误差时,如果解释变量是随机的,随 机误差项的正态性将得不到保证。 – 当模型遗漏了显著的变量,如果遗漏的变量是非正态 的随机变量,随机误差项将不具有正态性。 – 如果待估计的模型是原模型经过函数变换得到的,随 机误差项将不再服从正态分布

·正态性假设的违背: 一当模型存在被解释变量的观测误差,如果观测误差相 对于随机误差项的标准差特别大、样本长度又特别小, 随机误差项的正态性假设会导致显著性水平产生一定 程度的扭曲。 一当模型存在解释变量观测误差时,一般情况下,随机 误差项的正态性假设都是不能成立的;只有在回归函 数是线性的,且观测误差分布是正态的特殊情形下, 随机误差项的正态性才成立
• 正态性假设的违背: – 当模型存在被解释变量的观测误差,如果观测误差相 对于随机误差项的标准差特别大、样本长度又特别小, 随机误差项的正态性假设会导致显著性水平产生一定 程度的扭曲。 – 当模型存在解释变量观测误差时,一般情况下,随机 误差项的正态性假设都是不能成立的;只有在回归函 数是线性的,且观测误差分布是正态的特殊情形下, 随机误差项的正态性才成立

3.存在模型关系误差情况下的随机误差项 Y,=m(X1,β)+4i=1,2,.,n y,=m'(X,B)+y,i=1,2,.,n Y,=4+(m(X,B)-m'(X,B) i=1,2,.,n ·X是非随机的,V仍然是正态的。 ·X:是随机的,不能证明V仍然是正态的
3.存在模型关系误差情况下的随机误差项 • X i是非随机的 ,νi仍然是正态的 。 • X i是随机的 ,不能证明νi仍然是正态的 。 Yi = m(Xi ,) + i i =1,2, ,n Y m i n i i i ) 1,2, , ~ = (X , + = i i m i m i )) i 1,2, ,n ~ = + ( (X ,)) − (X , =

三、模型关系设定的指导原则
三、模型关系设定的指导原则