
计量经济检验:对模型基本假定的检验 基本假定违背:不满足基本假定的情况。 主要包括: (1)随机误差项序列存在异方差性: (2)随机误差项序列存在序列相关性; (3)解释变量之间存在多重共线性; (4)解释变量是随机变量且与随机误差项相关 (随机解释变量); 此外: (5)模型设定有偏误 (6)解释变量的方差不随样本容量的增而收敛
基本假定违背:不满足基本假定的情况。 主要包括: (1)随机误差项序列存在异方差性; (2)随机误差项序列存在序列相关性; (3)解释变量之间存在多重共线性; (4)解释变量是随机变量且与随机误差项相关 (随机解释变量); 此外: (5)模型设定有偏误 (6)解释变量的方差不随样本容量的增而收敛 计量经济检验:对模型基本假定的检验

§2.5异方差性 异方差的概念 二、异方差的类型 三、实际经济问题中的异方差性 四、异方差性的后果 五、异方差性的检验 六、异方差的修正 七、案例
§2.5 异方差性 一、异方差的概念 二、异方差的类型 三、实际经济问题中的异方差性 四、异方差性的后果 五、异方差性的检验 六、异方差的修正 七、案例

、异方差的概念 对于模型 Y,=B。+阝Xi+B2X2,+.+BkXa+4 如果出现 Var(u)=o2 即对于不同的样本点,随机误差项的方差不再 是常数,而互不相同,! 则认为出现了异方差性 (Heteroskedasticity)
对于模型 Yi = 0 + 1 Xi i + 2 X2i ++ k Xki + i 如果出现 Var i i ( ) = 2 即对于不同的样本点,随机误差项的方差不再 是常数,而互不相同,则认为出现了异方差性 (Heteroskedasticity)。 一、异方差的概念

异方差的概念 。异方差是相对于同方差而言的。 同方差:在经典线性回归模型的基本假定2中,随机扰 动项u的对每一个样本点的方差是一个等于σ2的常数, 即: ÷Var(u)=c2=常数 i=1,2,.,n ·异方差:是指随机扰动项u随着解释变量X的变化而变 化,即: Var(ui)=02 ;=02 f(Xi)i=1,2,.,n 。但u:仍然是一个服从正态分布的随机变量 异方差在横截面数据中比时间序列数据更为常见
❖ 异方差是相对于同方差而言的。 ❖ 同方差:在经典线性回归模型的基本假定2中,随机扰 动项ui的对每一个样本点的方差是一个等于 2的常数, 即: ❖ Var(ui)= 2=常数 i=1,2,.,n ❖ 异方差:是指随机扰动项ui随着解释变量Xi的变化而变 化,即: ❖ Var(ui)= 2 i = 2 f(Xi) i=1,2,.,n ❖ 但ui仍然是一个服从正态分布的随机变量 一、异方差的概念 异方差在横截面数据中比时间序列数据更为常见
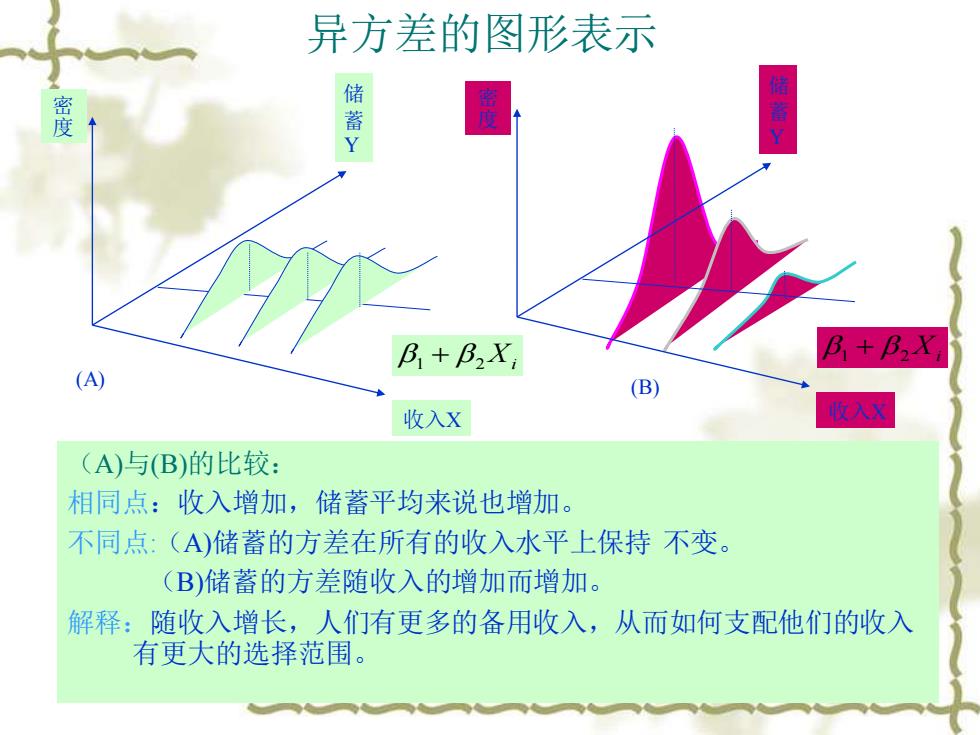
异方差的图形表示 密 储 蓄 度 度 B+B2X B+BX (A) (B) 收入X 收入X (A)与B)的比较: 相同点:收入增加,储蓄平均来说也增加。 不同点:(A)储蓄的方差在所有的收入水平上保持不变。 (B)储蓄的方差随收入的增加而增加。 解释:随收入增长,人们有更多的备用收入,从而如何支配他们的收入 有更大的选择范围
(A) (B) 密 度 储 蓄 Y 收入X 1 + 2 Xi 密 度 储 蓄 Y 收入X 1 + 2 Xi 异方差的图形表示 (A)与(B)的比较: 相同点:收入增加,储蓄平均来说也增加。 不同点:(A)储蓄的方差在所有的收入水平上保持 不变。 (B)储蓄的方差随收入的增加而增加。 解释:随收入增长,人们有更多的备用收入,从而如何支配他们的收入 有更大的选择范围

二、产生异方差的背景 1、按照边错边改学习模型(error-learning models),人们在学习的过程中,其行为误差 随时间而减少。在这种情况下,预料的会减少 例如,随着打字练习小时数的增加,不仅平均 打错个数而且打错个数的方差都有所下降。 2、随着收入的增长,人们有更多的备用收入, 从而如何支配他们的收入有更大的选择范围。 因此,在做储蓄对收入的回归时,很可能发现, 由于人们对其储蓄行为有更多的选择,与收入 俱增有关
二、产生异方差的背景 1、按照边错边改学习模型(error-learning models),人们在学习的过程中,其行为误差 随时间而减少。在这种情况下,预料的会减少。 例如,随着打字练习小时数的增加,不仅平均 打错个数而且打错个数的方差都有所下降。 2、随着收入的增长,人们有更多的备用收入, 从而如何支配他们的收入有更大的选择范围。 因此,在做储蓄对收入的回归时,很可能发现, 由于人们对其储蓄行为有更多的选择,与收入 俱增有关

二、产生异方差的背景 3、随着数据采集技术的改进,误差可能减少。 4、异方差还会因为异常值的出现而产生。一个 超越正常值范围的观测值或称异常值是指和其 它观测值相比相差很多(非常小或非常大)的 观测值。 5、回归模型的设定不正确也会造成异方差。例 如,在一个商品的需求函数中,若没有把有关 的互补商品和替代商品的价格包括进来(忽略 变量偏差),则回归残差就可能出现异方差
3、随着数据采集技术的改进,误差可能减少。 4、异方差还会因为异常值的出现而产生。一个 超越正常值范围的观测值或称异常值是指和其 它观测值相比相差很多(非常小或非常大)的 观测值。 5、回归模型的设定不正确也会造成异方差。例 如,在一个商品的需求函数中,若没有把有关 的互补商品和替代商品的价格包括进来(忽略 变量偏差),则回归残差就可能出现异方差。 二、产生异方差的背景

产生异方差的实例 1.服装需求函数 2.按收入分组数据的平均数 9.=f1p,.+u 建立的消费函数 i=1,2,.,n C,=B。+Bi,+u 没有考虑气候因素,气候 因为收入服从正态分布 对q的影响包含在u中 截面数据中高、低收入组的 高拿出更多钱适应气候 家庭数少于中收入组,因观 低正是“可怜老汉衣正单 察个数不同造成各组平均数 的方差呈现U型分布。(见下 心忧炭贱愿天寒” 图) 不同对q的需求偏离程度不 如果这种观测误差站随机误差项 同,u的方差随着收入增 的主要部分,那么将随收入 大而增大。 成规律变化
产生异方差的实例 1.服装需求函数 没有考虑气候因素,气候 对q的影响包含在ui中 高I拿出更多钱适应气候 低I正是“可怜老汉衣正单 心忧炭贱愿天寒” 不同I对q的需求偏离程度不 同,ui的方差随着收入增 大而增大。 2.按收入分组数据的平均数 建立的消费函数 因为收入I服从正态分布 截面数据中高、低收入组的 家庭数少于中收入组,因观 察个数不同造成各组平均数 的方差呈现U型分布。(见下 图) 如果这种观测误差站随机误差项 的主要部分,那么将随收入 成规律变化。 f( p ) u i n q I i i i i = , , + =1,2,, Ci Ii ui = + + 0 1
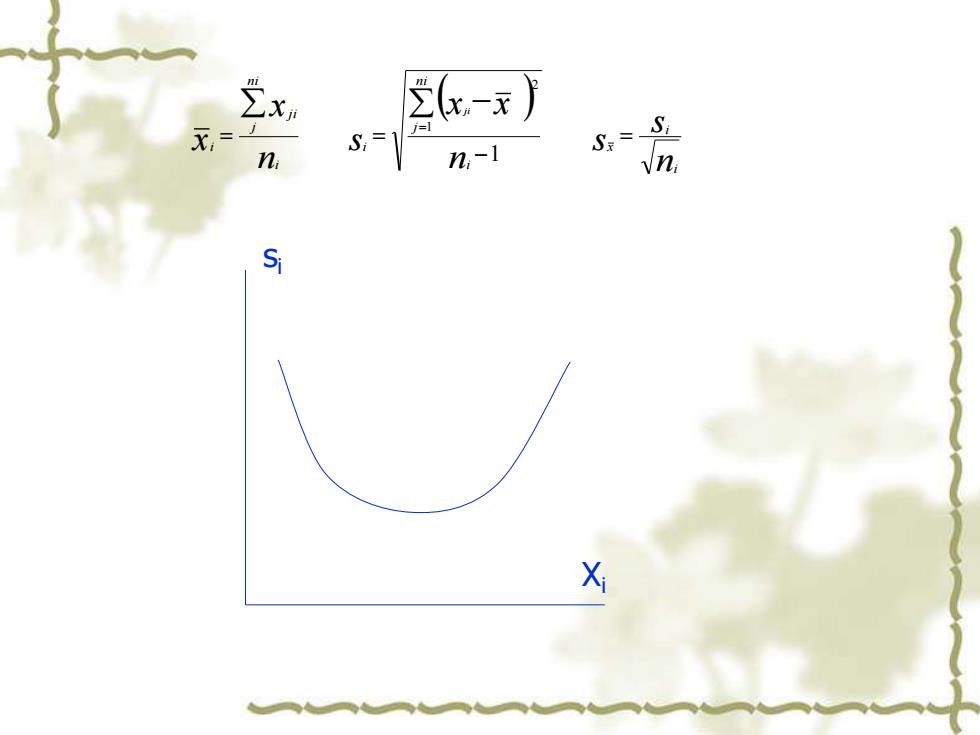
(-x月 n,-1 S-J n X
s i X i ( ) ns s nx x s nx x i i x i n i j i i n ij j i i ji = − = = − = 1 1 2

三、实际经济问题中的异方差性 例2.6.1:截面资料下研究居民家庭的储蓄行为 Y=Bo+B1X+1 Y:第个家庭的储蓄额X:第个家庭的可支配收入 高收入家庭:储蓄的差异较大 低收入家庭:储蓄则更有规律性,差异较小 的方差呈现单调递增型变化
三、实际经济问题中的异方差性 例2.6.1:截面资料下研究居民家庭的储蓄行为 Yi= 0+1Xi+i Yi :第i个家庭的储蓄额 Xi :第i个家庭的可支配收入 高收入家庭:储蓄的差异较大 低收入家庭:储蓄则更有规律性,差异较小 i的方差呈现单调递增型变化